 |
ЗАДАНИЕ №1. Вычислить указанные пределы.
|
|
|
|
Вариант 1.1) 
;2) 
Вариант 2.1) 
Вариант 3. 
.
Вариант 4. 
Вариант 5. 
.
Вариант 6. 
.
Вариант 7. 
.
Вариант 8.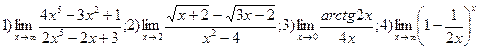 
.
Вариант 9. 
.
Вариант 10. 
.
Вариант 11. 
.
Вариант 12. 
.
Вариант 13. 
.
Вариант 14. 
.
Вариант 15. 
.
Вариант 16. 
.
Вариант 17.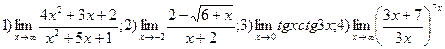 
.
Вариант 18. 
Вариант 19. 1) 
Вариант 20. 
Вариант 21. 1) 
Вариант 22. 1) 
Вариант 23. 
Вариант 24. 
Вариант 25. 
Вариант 26. 
Вариант 27. 
Вариант 28. 
Вариант 29. 
Вариант 30. 
ЗАДАНИЕ №2. Найти все точки разрыва функции y= f(x), если они существуют, и построить график функции.
Вариант 1. 
Вариант 2. 
Вариант 3. 
Вариант 4. 
Вариант 5. 
Вариант 6. 
Вариант 7. 
Вариант 8. 
Вариант 9. 
Вариант 10. 
Вариант 11. 
Вариант 12. 
Вариант 13. 
Вариант 14. 
Вариант 15. 
Вариант 16. 
Вариант 17. 
Вариант 18. 
Вариант 19. 
Вариант 20. 
Вариант 21. 
Вариант 22. 
Вариант 23. 
Вариант 24. 
Вариант 25. 
Вариант 27. 
Вариант 26. 
Вариант 28. 
Вариант 29. 
Вариант 30. 
ЗАДАНИЕ №3. Найти производные указанных функций.
Вариант 1. 
Вариант 2. 1) 
Вариант 3. 1) 
Вариант 4. 
Вариант 5. 
Вариант 6. 
Вариант 7. 
Вариант 8. 
Вариант 9. 
Вариант 10. 1) 
Вариант 11. 
Вариант 12. 
Вариант 13. 
Вариант 14. 
Вариант 15. 
Вариант 16. 
Вариант 17. 
Вариант 18. 
Вариант 19. 
Вариант 20. 
Вариант 21. 
Вариант 22. 
Вариант 23. 
Вариант 24. 
Вариант 25. 
.
Вариант 26. 
Вариант 27. 
Вариант 28. 
Вариант 29. 
Вариант 30. 
ЗАДАНИЕ №4. Известен закон движения точки. Найти скорость движения и ускорение в момент времени 
.
Вариант 1. 
Вариант 2. 
Вариант 3. 
Вариант 4. 
Вариант 5. 
Вариант 6. 
Вариант 7. 
Вариант 8. 
Вариант 9. 
Вариант 10. 
Вариант 11. 
Вариант 12. 
Вариант 13. 
Вариант 14. 
Вариант 15. 
Вариант 16. 
Вариант 17. 
Вариант 18. 
Вариант 19. 
Вариант 20. 
Вариант 21. 
Вариант 22. 
Вариант 23. 
Вариант 24. 
Вариант 25. 
Вариант 26. 
|
|
|
Вариант 27. 
Вариант 28. 
Вариант 29. 
Вариант 30. 
ЗАДАНИЕ №5. Найти пределы по правилу Лопиталя.
Вариант 1. 
Вариант 2. 1) 
Вариант 3. 
Вариант 4. 1) 
Вариант 5. 
Вариант 6. 
Вариант 7. 
Вариант 8. 
Вариант 9. 
Вариант 10. 1) 
Вариант 11. 
Вариант 12. 
Вариант 13. 
Вариант 14. 
Вариант 15. 
Вариант 16. 
Вариант 17. 
Вариант 18. 
Вариант 19. 
Вариант 20. 
Вариант 21. 
Вариант 22. 
Вариант 23. 
Вариант 24. 
Вариант 25. 
Вариант 26. 
Вариант 27. 
Вариант 28. 
Вариант 29. 
Вариант 30. 
ЗАДАНИЕ №6. Исследовать методами дифференциального исчисления функцию y=f(x). Построить график функции.
Этимологический словарь.
· Асимптота( греч. слово asymptotes – “несовпадающий”).
· График ( греч. слово graphikos- “начертанный”).
· Дифференциал ( лат. слово differento- “разность”). Одно из основных понятий математического анализа. Этот термин встречается у немецкого ученого Г. Лейбница в 1675 г. (опубликовано в 1684г.).
· Касательная ( лат.слово tangens – “касающийся”).
· Максимум (лат.слово maximum – “наибольшее”). Заимствовано во второй половине 19 в. из лат. яз.
· Минимум ( лат.слово minimum – “наименьшее”).
· Предел ( лат.слово limes – “граница”). Одно из основных понятий математики, означающее, что некоторая переменная величина в рассматриваемом процессе ее изменения неограниченно приближается к определенному постоянному значению. Термин ввел Ньютон, а употребляемый ныне символ lim (3 первые буквы от limes) – франц.ученый С.Люилье (1786 г.). Выражение lim первым записал У.Гамильтон (1853 г.).
· Производная ( франц.слово derivee). Ввел Ж.Лагранж в 1797 году.
· Функция ( лат. слово functio – “исполнение”, “совершение”). Одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Термин впервые появляется в 1692 г. у немецк. ученого Г.Лейбница притом не в современном понимании. Т., близкий к современному встречается у швейцарского ученого И.Бернулли (1718 г.). Обозначение функции f(x) ввел российский ученый Л.Эйлер (1734 г.).
|
|
|
· Экстремум( лат.слово exstremum – “крайнее”). Это общее название максимума и минимума функции.
Заключение.
Дифференциальное исчисление – это раздел математического анализа, связанный главным образом с понятиями производной и дифференциала функции. В дифференциальном исчислении изучаются правила вычисления производных и применения производных к исследованию свойств функций.
Функции мы всюду встречаем на практике, функции описывают движения, физические явления, они встречаются в технике, геометрии, механике, химии, биологии, экономике. Изучая функции, мы изучаем конкретные явления, которые они описывают. Одна и та же функция может описывать явления различной природы и тем самым объединять в себе закономерности, которым эти явления подчиняются.
В XVII веке математики уже умели вычислять мгновенную скорость и наклон касательной к кривой в разных частных случаях. Эти работы составили основу для создания общего математического анализа, но сначала они представляли собой разрозненные результаты, не объединенные общей теорией.
Общая теория была создана во второй половине XVII века в трудах великого английского математика Исаака Ньютона (1643-1727) и великого немецкого математика Готфрида Лейбница (1646-1716).
В XVIII веке крупнейшим представителям математического анализа был Леонард Эйлер (1707-1783) – академик Российской академии наук.
Понятия предела и понятия функции совершенствовались в XVIII веке, в частности, в трудах Эйлера.
Только в начале XIX века были окончательно созданы понятия предела последовательности чисел, предела функции, непрерывности функции, на которых основывается современный классический математический анализ. Обычно при этом отмечаются заслуги французского математика Огюстена Коши (1789-1857), которому принадлежат четкие формулировки указанных понятий.
Литература.
1. Алгебра и начала анализа: Учеб. Для 11 кл. общеобразоват. учреждений / Никольский С. М., Потапов М. К., Решетников Н. Н. – 2-е изд. – М.: Просвещение, 2003. – 448 с.
2. Баврин И. И. Высшая математика: Учебник для студентов естественнонаучных специальностей педагогических вузов. – М., 2000. – 616 с.
|
|
|
3. Байдак В. А. Система изучения свойств функций в школе. Пособие для учителей. Под ред. А. Д. Семушина. – Омск: Изд-во “Омская правда”, 1975. – 125 с.
4. Письменный Д. Т. Конспект лекций по высшей математике. 1 часть. – М.: Рольф, 2000. – 288 с.
5. Шипачев В. С. Высшая математика. – М., 1996. – 479 с.
|
|
|
