 |
Общая схема исследования функции.
|
|
|
|
1. Найти область определения функции (т.е. те значения, которые может принимать аргумент x). Обозначение: D(y).
2. Общие свойства функции.
а) чётность;
Функция называется чётной, если её область определения симметрична относительно x=0 и для любого x из области определения выполняется равенство: 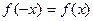 . Таким образом, точки графика с противоположными абсциссами имеют равные ординаты и график симметричен относительно оси Oy. Пример такой функции изображен на рис.17.Функция называется нечётной, если её область определения симметрична относительно x=0 и для любого x из области определения выполняется равенство:
. Таким образом, точки графика с противоположными абсциссами имеют равные ординаты и график симметричен относительно оси Oy. Пример такой функции изображен на рис.17.Функция называется нечётной, если её область определения симметрична относительно x=0 и для любого x из области определения выполняется равенство:  .Т.е. точки графика с противоположными абсциссами имеют противоположные ординаты, и график функции симметричен относительно начала координат
.Т.е. точки графика с противоположными абсциссами имеют противоположные ординаты, и график функции симметричен относительно начала координат
(рис.18).
|
 | |||
 | |||
|
Рис.17 Рис.18
б) периодичность;
Функция  называется периодической с периодом T, если для всех значений x из области определения выполняется равенство:
называется периодической с периодом T, если для всех значений x из области определения выполняется равенство:  .
.
в) точки пересечения с осями координат.
Замечание. Если исследование по какому-либо из пунктов а)-в) требует сложных вычислений или громоздких преобразований, то этот пункт исследования можно опустить.
3. Монотонность, экстремумы функции.
4. Направление выпуклости, точки перегиба.
5. Асимптоты.
6. Поведение функции на бесконечности
(найти 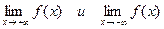 ).
).
7. Дополнительные точки.
Примеры. Исследовать функцию и построить график.
а) y=  .
.
Решение. 1) В нашем случае D(y)=(-µ;+µ), так как имеем многочлен третьей степени, графиком этой функции является кубическая парабола, она определена для любого значения х.
2) Исследуем функцию на четность и нечетность, периодичность, найдём нули функции.
|
|
|

Условия у(-х)=у(х) или у(-х)=-у(х) не выполняются, поэтому функция не является ни четной ни нечетной (или является функцией общего вида). Очевидно, функция непериодическая.
Найдем нули функции (для этого решим уравнение у =0).

1)  ; 2)
; 2) 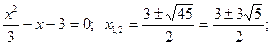
3) Исследуем функцию на монотонность и экстремум. Имеем
y¢= 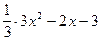 =
= 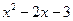 .
.
y¢=0,  .Исследуем знаки производной на интервалах, на которые область определения функции разбивается этими точками. Результаты представлены в таблице:
.Исследуем знаки производной на интервалах, на которые область определения функции разбивается этими точками. Результаты представлены в таблице:
| x | 
| -1 | 
| 
| |
| у¢ | + | - | + | ||
   y y
| 
| -9 |
Из таблицы видно, что умах=у(-1)=  ; уmin=у(3)=-9
; уmin=у(3)=-9
4) Найдём интервалы выпуклости, вогнутости графика, точки перегиба. На этом этапе исследования находим вторую производную. В данном случае: 
Исследуем знак у¢¢ на интервалах, на которые область определния разбивается этими точками. Результаты представлены в таблице:
| x | 
| 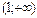
| |
 у¢¢ у¢¢
| - | + | |
   y y
| - 
|
Из таблицы видно, что промежуток  - промежуток выпуклости. Второй промежуток - интервал вогнутости, а точка (1; -
- промежуток выпуклости. Второй промежуток - интервал вогнутости, а точка (1; -  ) является точкой перегиба.
) является точкой перегиба.
5) Функциональное выражение функции - многочлен, а многочлены асимптот не имеют.
6). Исследуем поведение функции на бесконечности:
 ;
;

.
7) Построим график с учетом всего предыдущего исследования (при необходимости следует уточнить отдельные участки кривой, вычислив координаты нескольких дополнительных точек; рис19).
|


|



|
|
|
|
|



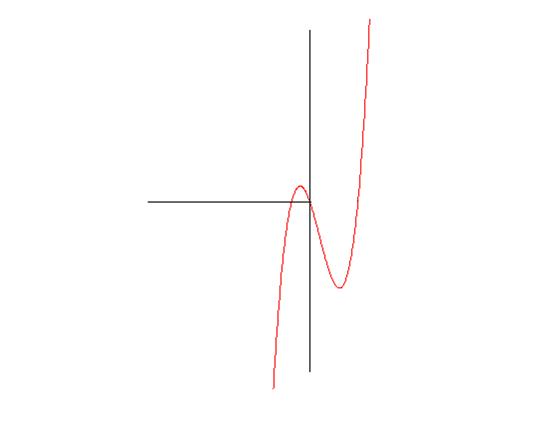
Рис.19
б) 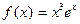
Решение.
1).  ;
;
2).  при
при  ;
;
3). Производная имеет вид  .
.
Решая неравенство f' (x) > 0, получаем: x  (- 3;0)
(- 3;0)  (0; +
(0; + 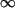 );
);
при x = 0 функция, очевидно, непрерывна, так что f (x) возрастает на объединённом интервале, то есть при x  (- 3; +
(- 3; + 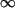 ). Решение неравенства f' (x) < 0 даёт только один интервал (-
). Решение неравенства f' (x) < 0 даёт только один интервал (- 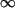 ; - 3); на нём функция убывает.
; - 3); на нём функция убывает.
| (-∞;-3) | -3 | (-3;0) | (0;+∞) | ||

| - | + | + | ||
   Y Y
| 
| min | - 
|
4). Найдем экстремумы функции. В точке 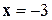 убывание функции сменяется возрастанием, значит, это точка локального максимума. Значение функции в этой точке равно
убывание функции сменяется возрастанием, значит, это точка локального максимума. Значение функции в этой точке равно 
|
|
|

Рис.20
Для более точного построения вычисляются дополнительные точки. Чертеж графика функции приведен на рис.20.
|
|
|





