Основы математического аппарата анализа и синтеза комбинационных логических устройств

 

Все устройства, оперирующие с двоичной информацией, подразделяются на два класса:

- комбинационные (дискретные автоматы без памяти).

- последовательные (дискретные автоматы с памятью).

Сигналы на выходах комбинационного устройства однозначно определяются сочетанием сигналов на его входах и не зависят от предыдущих состояний.

Примерами комбинационных устройств могут служить:

1) логические элементы, реализующие логический базис (логические функции И, ИЛИ, НЕ, а также И-НЕ или ИЛИ-НЕ)

2) электронные ключи;

3) мультиплексоры;

4) демультиплексоры и дешифраторы;

5) большинство арифметических устройств и т.д.

Основой анализа и синтеза логических устройств является алгебра логики (булева алгебра).

Связь между входными и выходными сигналами логических устройств устанавливает логическая функция.

 

Логическая функция

 

Функция f(x₁,x₂,x₃,...,x_n) называется логической (булевой, переключательной), если она, также как и ее аргументы, может принимать только два значения - “истинно” 1 или “ложно” 0.

Для n логических переменных (аргументов) существует 2ⁿ логических комбинаций из 0 и 1.

Например, для n = 2, x₁x₂ = 00, 01, 10, 11.

Для каждой комбинации переменных набора логическая функция может принимать значение 0 или 1. Для n переменных существует  различных логических функций.

Логическая функция может быть задана:

1) словесно;

2) таблицей истинности;

3) алгебраически;

4) графически.

Пример словесного описания: функция f(x₁,x₂) принимает значение 1, когда значения переменных равны: x₁ = x_2. При неравенстве переменных x₁¹x₂ функция принимает значение 0.

Эту функцию представляют также табл.1.1, которая содержит все 2ⁿ возможных наборов значений логических переменных (аргументов) и значения функции, соответствующие каждому из наборов.

 

Таблица 1.1

Таблица истинности.

x1	x2	f
0	0	1
0	1	0
1	0	0
1	1	1

Алгебраическое представление логической функции в совершенной нормальной форме

Различают две формы алгебраического представления логической функции:

  совершенная дизъюнктивная нормальная форма (СДНФ);

  совершенная конъюнктивная нормальная форма (СКНФ).

Для перехода от табличного представления функции к алгебраическому в виде ее СДНФ каждому i-ому набору переменных ставится в соответствие минтерм (m_i) (константа единицы) - конъюнкция переменных, которые входят либо в прямом виде, если значение данной переменной в наборе равно 1, либо в инверсном виде, если значение переменной равно 0. Для n переменных составляют q=2ⁿ минтермов: m₀, m₁,..., m_q-1.

Алгебраическое выражение логической функции в форме СДНФ представляют в форме суммы:

 

,

 

где f_i, m_i - значение функции (0 или 1) и минтерм, соответствующий i- ому набору переменных.

Для перехода от табличного представления функции к алгебраическому в виде СКНФ каждому i-ому набору переменных ставится в соответствие макстерм (M_i) - дизъюнкция переменных, которые входят либо в прямом виде, если значение данной переменной равно 0, либо в инверсном виде, если значение переменной равно 1 [1].

Алгебраическое выражение логической функции в форме СКНФ представляют в виде произведения

 

,

 

где f_i, M_i - значение функции и макстерм, соответствующий i-ому набору переменных.

Пример 1.1. Логическая функция равнозначность (эквивалентность) для двух переменных представлена табл.1.2.:

Таблица 1.2.

Таблица истинности

x1	x2	f
0	0	1
0	1	0
1	0	0
1	1	1

 

Представить эту функцию в алгебраической форме в виде СДНФ и СКНФ.

Решение. 1. Для n=2 переменных составляют q = 2ⁿ = 4 минтерма и макстерма, которые вписаны соответственно в 3-ю и 4-ю графы табл.1.3.

 

Таблица 1.3

Минтермы и макстермы

x1	x2	mi	Mi	f
1	2	3	4	5
0	0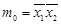
0	1
1	0
1	1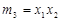

 

2. Алгебраическое представление логической функции в СДНФ

 

 

3. Алгебраическое представление логической функции в СКНФ

 

 

Ускорить процесс нахождения СДНФ и СКНФ можно, если применить другие правила.

СДНФ находят по правилу записи логической функции “по единицам”:

выписывают ряд произведений всех аргументов и соединяют их знаками дизъюнкции; количество произведений должно равняться числу наборов, на которых заданная функция обращается в единицу;

записывают под каждым произведением набор аргументов, на котором функция равна единице, и над аргументами равными 0, ставят знаки отрицания.

Пример 1.2. Представить в СДНФ логическую функцию пяти аргументов f(x₁,x₂,x₃,x₄,x₅), равную единице на следующих четырех наборах

 

0	0	1	0	1
0	1	1	1	1
1	0	0	0	0
1	1	1	1	1

Решение. 1. Запишем четыре произведения аргументов, связанных знаком дизъюнкции, и под каждым из них - один из перечисленных наборов

 

x1 x2 x3 x4 x5 Ú x1 x2 x3 x4 x5 Ú x1 x2 x3 x4 x5 Ú x1 x2 x3 x4 x5

0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1

 

2. Расставляя отрицания над аргументами, равными нулю, получим СДНФ логической функции:

 

Ú Ú Ú

СКНФ находят по правилу записи переключательной функции “по нулям”:

1) выписывают произведения дизъюнкций всех аргументов с количеством сомножителей, равным числу наборов, на которых заданная функция обращается в нуль;

2) записывают под каждым сомножителем набор аргументов, на котором функция равна нулю, а над аргументами, равными единице ставят знаки отрицания.

Пример 1.3. Представить в СКНФ переключательную функцию четырех аргументов f(x₁,x₂,x₃,x₄), равную нулю на наборах

 

0	0	1	1
0	1	1	1
1	0	0	0
1	1	1	1

 

Решение. 1. Запишем четыре произведения дизъюнкций всех аргументов и под каждым из них один из перечисленных наборов:

 

(x1Úx2Úx3Úx4) × (x1Úx2Úx3Úx4) × (x1Úx2Úx3Úx4) × (x1Úx2Úx3Úx4)

0 0 1 1 0 1 1 1 1 0 0 0 1 1 1 1

 

2. Расставляя знаки отрицания над аргументами, равными единице, получим СКНФ логической функции:

 

 

При выборе совершенной формы записи логической функции следует иметь в виду, что СДНФ является более целесообразной, если число наборов, на которых функция равна 0, превышает число наборов, на которых функция равна 1. В противоположном случае более приемлемой будет СКНФ.

Пример 1.4. Необходимо построить мажоритарную ячейку (ячейку голосования) на три входа, т.е. такую ячейку, у которой сигнал на выходе равен единице тогда, когда большинство входных сигналов равно единице, т.е. он равен единице, когда на двух или трех входах присутствует сигнал единицы, в противном случае выходной сигнал равен нулю [2].

Представить логическую функцию мажоритарной ячейки в виде таблицы истинности и в алгебраическом виде в формах СДНФ и СКНФ.

Решение. 1. Для трех входных сигналов, т.е. для n=3 переменных существует q=2ⁿ=2³=8 различных комбинаций этих сигналов табл.1.4.

 

Таблица 1.4

Таблица истинности

x1	x2	x3	f
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

 

2. Для представления логической функции в алгебраическом виде в форме СДНФ нужно представить эту функцию в виде суммы логических произведений аргументов, соответствующих тем строкам таблицы истинности, для которых логическая функция равна единице. При записи этих логических произведений следует брать соответствующий аргумент с инверсией, если этот аргумент в данной строке таблицы равен нулю, и без инверсии, если он равен единице:

 

 

3. Для представления логической функции в алгебраическом виде в форме СКНФ нужно представить эту функцию в виде произведения логических сумм аргументов, соответствующих тем строкам таблицы истинности, для которых логическая функция равна нулю. При записи этих логических сумм следует брать соответствующий аргумент с инверсией, если этот аргумент в данной строке таблицы равен единице, и без инверсии, если он равен нулю:

 

Пример 1.5. Полный набор 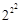= 16 логических функций двух переменных приведен в табл.1.5. Записать алгебраические выражения этих функций в формах СДНФ и СКНФ.

 

Таблица 1.5

Полный набор логических функций двух переменных

	Таблица истинности					Название функции	Условное обозначение	Алгебраическое выражение
Функция	x1	0	0	1	1
	x2	0	1	0	1			СДНФ	СКНФ
1		2	3	4	5	6	7	8	9
f0		0	0	0	0	Константа нуль	0
f1		0	0	0	1	Конъюнкция	x1 x2
f2		0	0	1	0	Запрет по x2	x1  x2 x1  x2
f3		0	0	1	1	Тождественность x1	x1
f4		0	1	0	0	Запрет по x1	x2  x1 x2  x1
f5		0	1	0	1	Тождественность x2	x2
f6		0	1	1	0	Исключающее ИЛИ Сумма по модулю 2	x1 x2
f7		0	1	1	1	Дизъюнкция	x1 Ú x2 x1 + x2
f8		1	0	0	0	Стрелка Пирса	x1 ¯ x2
f9		1	0	0	1	Равнозначность	x1 ~ x2
f10		1	0	1	0	Инверсия x2
f11		1	0	1	1	Импликация от x2 к x1	x2 ® x1
f12		1	1	0	0	Инверсия x1
f13		1	1	0	1	Импликация от x1 к x2	x1 ® x2
f14		1	1	1	0	Штрих Шеффера	x1 / x2
f15		1	1	1	1	Константа единицы	1

Предыдущая12345678Следующая

Поделиться:

Воспользуйтесь поиском по сайту: