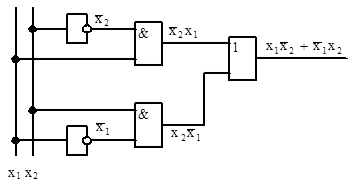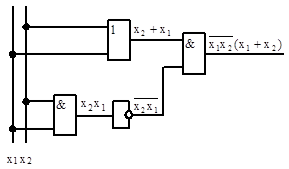|
Взаимное соответствие логической функции и логической схемы
|
|
|
|
По заданной логической функции f(х1, х2, х3,...,хn) можно составить электрическую схему, которая будет преобразовывать логические сигналы х1, х2, х3,...,хn согласно указанной функции.
Различают схемы:
1) структурные;
2) функциональные;
3) принципиальные (полные).
Структурная схема определяет основные функциональные части, их назначение и взаимосвязи. Структурная схема концентрирует в себе все наиболее важное и существенное о составе, структуре и функциях электронного устройства (ЭУ). Электронным устройством называют любую совокупность взаимодействующих электрорадиоэлементов, предназначенную для выполнения заданной функции.
Функциональная схема разъясняет процессы, протекающие в отдельных цепях или в целом ЭУ. Она занимает промежуточное место между структурной и принципиальной схемами. Цепи, в которых хотят разъяснить процессы, показывают так же подробно, как и на принципиальной схеме, а другие функциональные части изображают в виде прямоугольников, как и на структурной схеме.
Принципиальная (полная) схема определяет полный состав элементов и связей между ними и дает детальное представление о принципах работы ЭУ.
Существуют два уровня, на которых разрабатывают указанные три вида схем:
1) микроуровень;
2) макроуровень.
На микроуровне разрабатывают схемы для интегральных микросхем (ИМС). Эти схемы создают разработчики ИМС, они входят в состав документации на ИМС и приводятся в справочниках и технической литературе.
К структурным схемам цифровых ИМС относят схемы, на которых представлены ее части, более крупные, чем функциональные элементы. Функциональный элемент - наименьшая единица функциональной структуры, которая при технической реализации может быть выполнена в виде электрической законченной схемы, выполняющей определенную функцию. Структурные схемы разрабатывают для больших (БИС) и сверхбольших (СБИС) интегральных схем. На этом уровне интеграции разработка функциональных схем для использования лишена смысла ввиду их сложности. О правильности функционирования БИС и СБИС судят по значениям логических сигналов на их выходах при тестировании.
|
|
|
Для ИМС среднего (СИС) и малого (МИС) уровня интеграции разрабатывают функциональные схемы. Структурными элементами функциональных схем комбинационных систем являются логические элементы. Логические элементы различаются между собой характером реализуемой функции, числом входов (по числу одновременно действующих переменных), числом выходов и другими признаками. Работа их оценивается только с точки зрения логики, без учета практического воплощения (технической базы, способа питания и т.п.). Структурными элементами функциональных схем последовательных систем (системы с памятью) являются триггеры и логические элементы.
Функции, выполняемые логическими элементами и триггерами, могут быть определены по их условным графическим обозначениям. К функциональным относятся такие схемы, на которых одна из нескольких одинаковых частей показана на уровне логических элементов (и триггеров), и остальные - в виде более крупных структур.
Структурная и функциональная схемы не дают представления о физических процессах в логических элементах. Эти представления для каждой серии ИМС дают принципиальные схемы их базовых логических элементов.
На схемах логические элементы по ГОСТ 2.743-82 "Обозначения условные графические в схемах. Элементы цифровой техники" изображают прямоугольником, в верхней части которого указывают символ функции: & для И; 1 для ИЛИ. Инверторные входы и выходы выделяются кружком у вывода. Выводы питания и общий не показывают.
|
|
|
Рассмотрим порядок составления функциональной схемы (рис.3.1) по заданной логической функции, например,
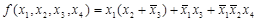
1-й этап - получить отрицание от переменных х1, х2, х3.
2-й этап - получить дизъюнкцию 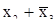 , конъюнкции
, конъюнкции 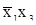 и
и 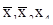 .
.
3-й этап - получить конъюнкцию х1(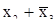 ).
).
 |
4-й этап - получить заданную логическую функцию.
Рис. 3.1 Функциональная схема.
Проектирование функциональных схем сводится к последовательным формальным процедурам, которые могут быть реализованы на ЭВМ. Способ соединения логических элементов функциональной схемы определяется последовательностью выполнения логических операций в заданной логической функции. Последовательность выполнения этих операций удобно разбить на ряд этапов. В каждый этап включают те операции, которые можно проводить в произвольной последовательности.
Пример 3.1. Синтезировать в базисе И, ИЛИ, НЕ и в базисе И-НЕ, ИЛИ-НЕ устройство, сигнал на выходе которого равен 1 только в том случае, когда на его двух входах (х1 и х2) действуют различные сигналы (узел неравнозначности, сумматор по модулю два).
Решение: 1. Таблица истинности в соответствии со словесным описанием работы устройства:
| х1 | х2 | f |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
2.Для перехода от табличного представления функции к алгебраическому в формах СДНФ и СКНФ каждому набору переменных ставятся в соответствие минтермы (mi) и макстермы (Mi):
| х1 | х2 | mi | Mi | f |
| 0 | 0 | 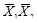
| 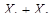
| 0 |
| 0 | 1 | 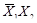
| 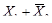
| 1 |
| 1 | 0 | 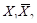
| 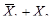
| 1 |
| 1 | 1 | 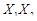
| 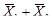
| 0 |
3. СДНФ функции:
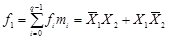 ,
,
где q=2n, n - число переменных.
4. СКНФ функции:
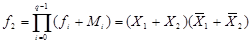 .
.
Применив правило Де Моргана: 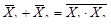 , получим:
, получим:
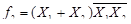
4. Функциональная схема для функции, представленной в СДНФ, в базисе И, ИЛИ, НЕ (рис.3.2).
|
|
Рис. 3.2 Функциональная схема устройства в базисе И, ИЛИ, НЕ
6. Функциональная схема для функции, представленной в СКНФ, в базисе И, ИЛИ, НЕ (рис.3.3).
|
|
Рис. 3.3 Функциональная схема устройства в базисе И, ИЛИ, НЕ
7. Для использования базиса И-НЕ, ИЛИ-НЕ преобразовывают далее полученные логические функции. Применяют закон двойной инверсии:
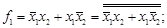

В соответствии с законами Де Моргана (инверсии; принципа дуальности, двойственности):
|
|
|
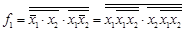 ;
;
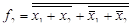 .
.
8. Функциональная схема для реализации функции f1 (рис.3.4).
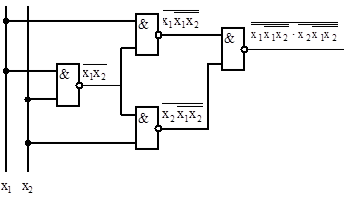
Рис.3.4 Функциональная схема для реализации функции f 1
9. Функциональная схема для реализации функции f2 (рис.3.5).
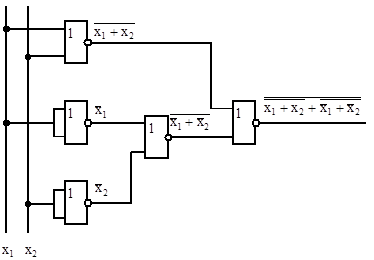
Рис.3.5 Функциональная схема для реализации функции f 2
Пример 3.2. Синтезировать в базисе И, ИЛИ, НЕ и в базисе И-НЕ, ИЛИ-НЕ устройство, сигнал на выходе которого равен 1, только в том случае, когда на его двух входах (х1, х2) действуют одинаковые сигналы (узел равнозначности).
Решение. 1. Таблица истинности в соответствии со словесным описанием работы устройства:
| х1 | х2 | f |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2. Определяют минтермы mi и макстермы Mi:
| х1 | х2 | mi | Mi | f |
| 0 | 0 | 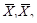
| 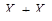
| 1 |
| 0 | 1 | 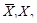
| 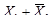
| 0 |
| 1 | 0 | 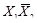
| 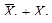
| 0 |
| 1 | 1 | 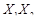
| 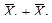
| 1 |
3. СДНФ функции:
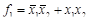 .
.
Применив закон Де Моргана, получают:
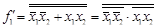 .
.
4. СКНФ функции:
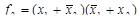 .
.
В соответствии с законом Де Моргана:
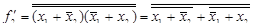 .
.
5. Функциональная схема для f1 (рис.3.6).
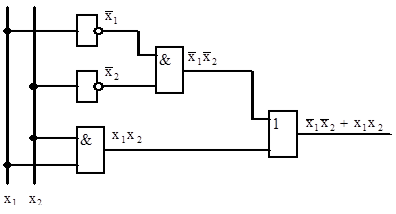
Рис.3.6 Функциональная схема для f 1
6. Функциональная схема для 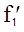 (рис.3.7).
(рис.3.7).
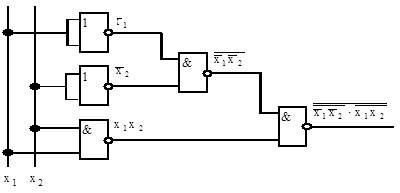
Рис. 3.7 Функциональная схема для 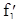
7. Функциональная схема для f2 (рис.3.8).
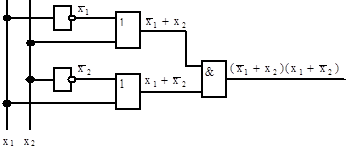
Рис. 3.8 Функциональная схема для f 2
8. Функциональная схема для 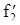 (рис.3.9).
(рис.3.9).
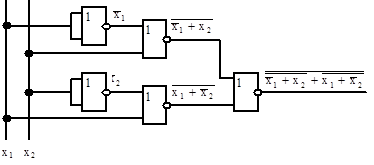
Рис.3.9 Функциональная схема для 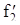
Все четыре функциональные схемы логически равноценны.
Пример 3.3. Устройство с четырьмя входами должно работать так, чтобы на выходе появился сигнал 1, когда не менее чем на трех входах будут одновременно сигналы 1. Синтезировать устройство на элементах И, ИЛИ, НЕ.
Решение. 1. Таблица истинности в соответствии со словесным описанием работы устройства:
Таблица 3.1
Таблица истинности
| Номер набора | х1 | х2 | х3 | х4 | f |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 1 | 1 | 1 |
2. Запишем СДНФ функции на основе ее единичных наборов:
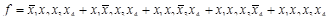 .
.
3.Для минимизации функции применим карту Карно (рис.3.10).
|
|
|
| х1х2 х3х4 | 00 | 01 | 11 | 10 |
| 00 | 0 | 0 | 0 | 0 |
| 01 | 0 | 0 |  1 1
| 0 |
| 11 | 0 |  1 1
| 1 | 1 |
| 10 | 0 | 0 | 1 | 0 |
Рис. 3.10 Карта Карно
4. МНДФ функции:
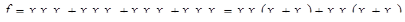 .
.
5. Функциональная схема устройства (рис.3.11).
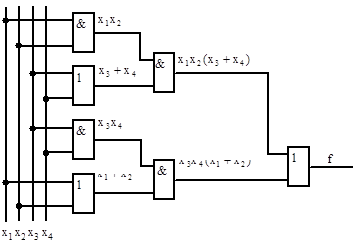
Рис.3.11 Функциональная схема устройства
Пример 3.4. Синтезировать мажоритарный элемент на три входа в базисе ИЛИ-НЕ. У такого элемента значение выходного сигнала совпадает с значением большинства входных.
Решение. 1. Таблица истинности в соответствии со словесным описанием работы элемента:
| x1 | x2 | х3 | у |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2. СДНФ функции на основе ее единичных наборов:
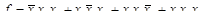 .
.
3. Для минимизации функции применим карту Карно (рис.3.12).
| х1х2 х3 | 00 | 01 | 11 | 10 |
 0 0
|   0 0
| 0 |  1 1
|  0 0
|
| 1 | 0 |  1 1
| 1 | 1 |
Рис.3.12 Карта Карно
4. МДНФ функции:
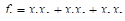 .
.
5. МКНФ функции:
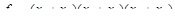 .
.
6. Для реализации функции в базисе И-НЕ и в базисе ИЛИ-НЕ преобразуем функцию в соответствии с законом Де Моргана:
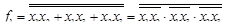 ;
; 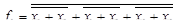 .
.
7. Функциональная схема для функции f1 в базисе И-НЕ (рис.3.13).
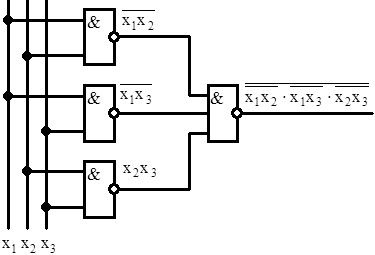
Рис.3.13 Функциональная схема для функции f1 в базисе И-НЕ
8. Функциональная схема для функции f2 в базисе ИЛИ-НЕ (рис.3.14).
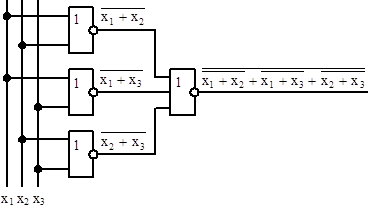
Рис.3.14 Функциональная схема для функции f2 в базисе ИЛИ-НЕ
|
|
|