 |
Аналитические методы минимизации логических функций
|
|
|
|
Эти методы базируются на применении основных законов булевой алгебры.
Алгоритм получения МДНФ логической функции:
1. Логическая функция представляется в СДНФ. Причем, если она задана таблицей истинности, то представляют путем записи “по единицам”; если она задана алгебраической произвольной дизъюнктивной форме - путем применения операций развертывания, формул Де Моргана и др.
2. В полученном СДНФ проводят все возможные операции неполного склеивания и затем поглощения. В результате получают сокращенную дизъюнктивную нормальную форму, т.е. дизъюнкцию самых коротких из всех возможных элементарных произведений (простые импликанты), входящие в данную логическую функцию.
3. Находят минимальные дизъюнктивные нормальные формы по импликантной матрице.
Импликантная матрица - это таблица, на вертикальные и горизонтальные входы которой записывают соответственно члены СДНФ и простые импликанты заданной логической функции.
Клетки импликантной матрицы, образованные пересечением строк с импликантами и столбцов с поглощательными ими членами СДНФ, отмечают крестиками [5].
МДНФ находят как дизъюнкцию минимального числа импликант, которые совместно накрывают крестиками все колонки импликантной матрицы.
Пример 1.10. Минимизировать логическую функцию:
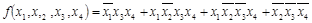
Решение: 1. Функция задана в алгебраической форме, применяя операции развертывания
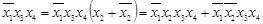

получают СДНФ, содержащую шесть членов:

2. Операции склеивания проводят в следующем порядке:
1) выполняются все возможные склеивания 1-ого члена с остальными;
2) выполняются все возможные склеивания 2-ого члена с остальными, кроме 1-ого;
3) выполняются все возможные склеивания 3-ого члена с остальными, кроме 1-ого и второго и т.д.
|
|
|
Склеиваться могут только те члены, у которых число переменных с отрицаниями отличается на единицу. Результаты склеивания и поглощения:

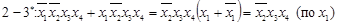



Звездочками отмечают те члены СДНФ, которые поглощаются произведениями, образовавшимися после склеивания.
В рассматриваемом примере поглощаются все шесть исходных членов, поэтому СДНФ заданной функции имеет вид:

К этому выражению операции склеивания и поглощения применить нельзя, и, следовательно, оно является сокращенной дизъюнктивной нормальной формой логической функции, а его члены - простыми импликантами.
3. Строят для заданной функции импликантную матрицу (табл.1.9)
Таблица 1.9
Импликантная матрица
| Простые | Члены СДНФ | |||||
| импликанты (минтермы) | 
| 
| 
| 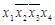
| 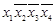
| 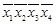
|
| 1 | 2 | 3 | 4 | 5 | 6 | |
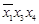
| X | X | ||||
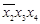
| X | X | ||||

| X | X | ||||

| X | X | ||||
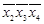
| X | X | ||||
Для получения МДНФ необходимо найти минимальное число импликант, которые совместно накрывают крестиками все столбцы импликантной матрицы:

Сложность логической функции определяется числом переменных входящих в ее выражение: в заданной функции 14, в минимальной - 9.
Первый алгоритм получения МКНФ логической функции:
1. Логическую функцию представляют в СКНФ. Причем, если она задана таблицей истинности, то ее записывают “ по нулям”; если она задана алгебраически в произвольной конъюктивной форме, то для записи в СКНФ выполняют все возможные операции развертывания.
2. В полученной СКНФ выполняют все возможные операции неполного склеивания и затем поглощения. В результате получают сокращенную конъюнктивную нормальную форму, члены которой являются простыми макстермами.
3. МКНФ находят по макстермной матрице.
Пример 1.11. Логическая функция задана табл.1.10
|
|
|
Таблица 1.10
Таблица истинности
| x1 | x2 | x3 | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Найти МКНФ этой функции.
Решение:
1. Выписывают заданную функцию в СКНФ “по нулям” таблицы истинности:
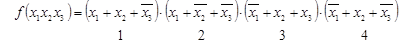
2. Проводят операции склеивания и поглощения:
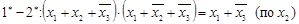

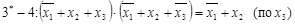
В данном примере поглощаются все четыре члена исходного выражения и, следовательно, СКНФ
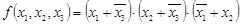
3. Макстермная матрица задана табл.1.11
Таблица 1.11
Макстермная матрица
| Простые импликанты | Члены СКНФ | |||

| 
| 
| 
| |
| (макстермы) | 1 | 2 | 3 | 4 |

| X | X | ||
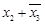
| X | X | ||
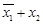
| X | X | ||
4. МКНФ логической функции:
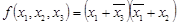 .
.
Второй алгоритм получения МКНФ логической функции:
1. Логическая функция представляется в СДНФ заданной функцией, взятой с отрицанием.
Если функция задана таблицей истинности, то выписывают ряд произведений всех аргументов и соединяют их знаками дизъюнкции; количество произведений должно равняться числу наборов, на которых заданная функция обращается в нуль; под каждым произведением записывают набор аргументов, на которых функция равна нулю, и над аргументами, равными нулю, ставят знаки отрицания. Если функция заданна алгебраически в произвольной форме, то сначала находят ее СДНФ, а затем записывают дизъюнкцию всех произведений аргументов, которые не вошли в СДНФ.Находят МДНФ по рассмотренному выше алгоритму. От полученной МДНФ берут отрицание и, после преобразований по формулам Де Моргана, получают МКНФ.
Пример 1.12. Найти МКНФ, функции заданной табл.1.12
Таблица 1.12
Таблица истинности
| x1 | x2 | x3 | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Решение: 1. СДНФ, взятая с отрицанием:
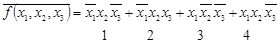
2. Результаты склеивания и поглощения:


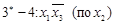
3. МДНФ, взятая с отрицанием:

4. Взяв от обеих частей последнего равенства отрицание и применив формулу Де Моргана, получают МКНФ логической функции:
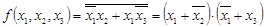 .
.
Логический базис
Любую логическую функцию можно представить в виде СДНФ или СКНФ, т.е. с помощью соответствующей комбинации простейших логических функций И, ИЛИ, НЕ. Такой набор простейших логических функций называют функционально полным или логическим базисом.
|
|
|
Логический базис называют минимальным, если удаление хотя бы одной из входящих в него функций превращает его в функционально неполный.
Логический базис И, ИЛИ, НЕ не является минмальным, так как с помощью закона дуальности (Де Моргана) можно исключить из логических выражений либо функцию И, либо функцию ИЛИ:

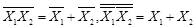 .
.
В результате получим минимальные базисы: И, НЕ и ИЛИ, НЕ.
|
|
|


