 |
Распределение Максвелла по проекциям скорости.
|
|
|
|
Распределение Максвелла по проекциям скорости.
Когда проводится экспериментальная проверка распределения Максвелла, то регистрируются молекулы, летящие в одну сторону. Чтобы получить функцию распределения молекул по проекциям скорости перепишем распределение Максвелла в виде
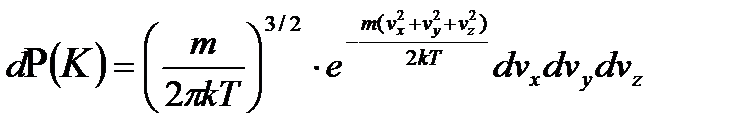 (2. 32)
(2. 32)
Эту вероятность можно представить в виде произведения 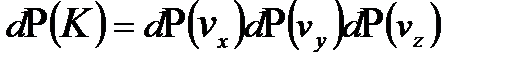 , где каждый из сомножителей представляет собой распределение Максвелла для проекций скорости молекул. Очевидно, что
, где каждый из сомножителей представляет собой распределение Максвелла для проекций скорости молекул. Очевидно, что
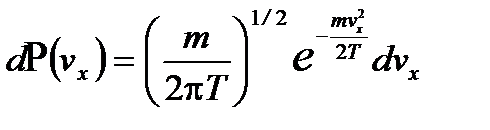 . (2. 33)
. (2. 33)
Легко увидеть, что плотность вероятности 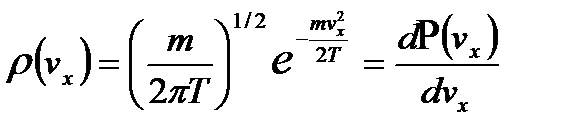 симметрично относительно начала координат и имеет максимум при vx = 0. Положительные и отрицательные значения vx имеют одинаковую вероятность, поэтому наиболее вероятная проекция и средняя проекция скорости равны нулю
симметрично относительно начала координат и имеет максимум при vx = 0. Положительные и отрицательные значения vx имеют одинаковую вероятность, поэтому наиболее вероятная проекция и средняя проекция скорости равны нулю 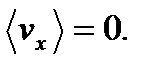 Можно пояснить на простых картинках фазового объема различие в распределениях по абсолютным значениям скорости и по их проекциям, а также, почему наиболее вероятная проекция скорости равна нулю. Плотность числа точек наибольшая в центре системы координат скоростей, а затем падает по экспоненте -
Можно пояснить на простых картинках фазового объема различие в распределениях по абсолютным значениям скорости и по их проекциям, а также, почему наиболее вероятная проекция скорости равна нулю. Плотность числа точек наибольшая в центре системы координат скоростей, а затем падает по экспоненте - 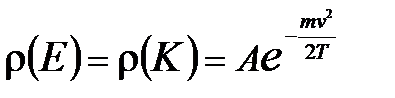 . Для абсолютных значений скорости фазовый объем растет с увеличением абсолютного значения скорости пропорционально ~ 4pv2dv. Поэтому при малых скоростях распределение растет из-за фазового объема, достигает максимума и затем падает из-за быстрого падения плотности частиц (хотя фазовый объем по -прежнему растет).
. Для абсолютных значений скорости фазовый объем растет с увеличением абсолютного значения скорости пропорционально ~ 4pv2dv. Поэтому при малых скоростях распределение растет из-за фазового объема, достигает максимума и затем падает из-за быстрого падения плотности частиц (хотя фазовый объем по -прежнему растет).
Если рассматривать фазовый объем в распределении по проекциям скорости, то этот фазовый объем постоянен для всех значений vx, и равен dvx. Следовательно, вероятность больше там, где больше плотность частиц.
|
|
|
Вычислим среднюю энергию, приходящуюся на одну степень свободы, т. е. сосчитаем 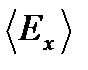 - долю кинетической энергии, относящуюся к движению по оси x. По определению
- долю кинетической энергии, относящуюся к движению по оси x. По определению
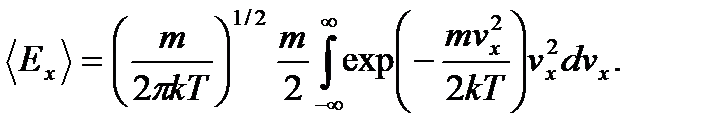
Так как 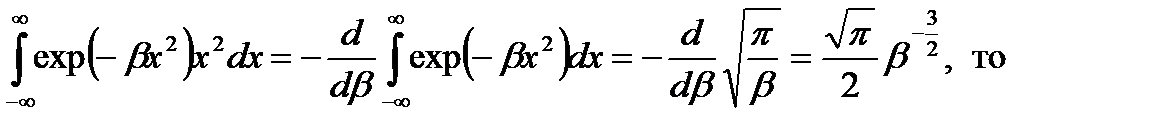
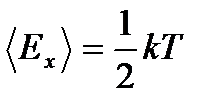 . (2. 34)
. (2. 34)
Итак, кинетическая энергия, приходящаяся на одну степень свободы, равна “половинке” kT, причем 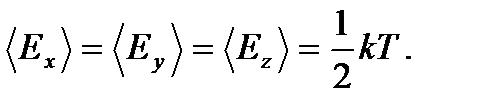 Тогда среднее значение полной энергии равно
Тогда среднее значение полной энергии равно
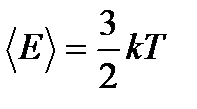 . (2. 35)
. (2. 35)
§2. 3. Распределение Больцмана и его свойства.
В начале настоящей главы мы писали для классической подсистемы 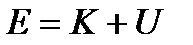 , и поскольку кинетическая энергия есть функция скоростей, а потенциальная энергия - функция координат, то вероятность для подсистемы иметь энергию Е равна
, и поскольку кинетическая энергия есть функция скоростей, а потенциальная энергия - функция координат, то вероятность для подсистемы иметь энергию Е равна 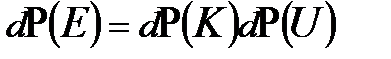 . В силу независимости событий (произведение вероятностей) иметь определенные значения кинетической и потенциальной энергий можно рассматривать отдельно вероятность распределения частиц во внешнем поле
. В силу независимости событий (произведение вероятностей) иметь определенные значения кинетической и потенциальной энергий можно рассматривать отдельно вероятность распределения частиц во внешнем поле 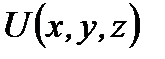
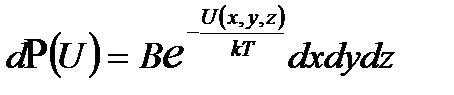 , (2. 36)
, (2. 36)
Так как 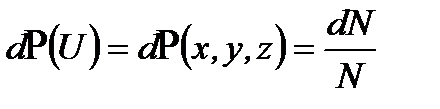 , то число молекул в объеме
, то число молекул в объеме  определяется формулой
определяется формулой 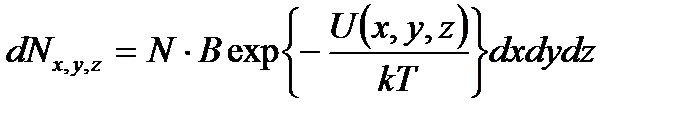 . Смысл множителя NB легко понять, если рассмотреть число частиц в единице объема, т. е. плотность (концентрацию) числа частиц
. Смысл множителя NB легко понять, если рассмотреть число частиц в единице объема, т. е. плотность (концентрацию) числа частиц 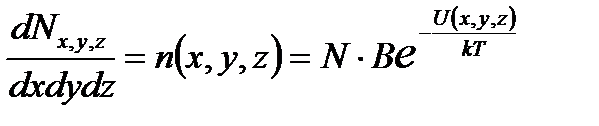 . Очевидно, что произведение NB равно плотности числа частиц
. Очевидно, что произведение NB равно плотности числа частиц 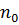 в точке, где U = 0. Тогда
в точке, где U = 0. Тогда
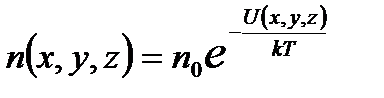 . (2. 37)
. (2. 37)
Эта формула носит название распределения Больцмана.
Если отсчет вести от точки, где 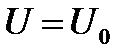 , то распределение Больцмана принимает вид
, то распределение Больцмана принимает вид
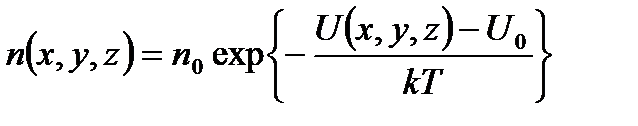 . (2. 38)
. (2. 38)
Примеры использования распределения Больцмана:
1) Распределение частиц в сосуде по высоте в однородном поле тяжести (  ). Для Земли поле тяжести однородно для небольших высот h < < R3 (R3 - радиус Земли):
). Для Земли поле тяжести однородно для небольших высот h < < R3 (R3 - радиус Земли):
| h |
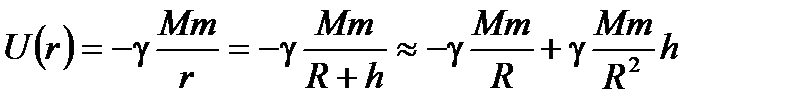 ,
,
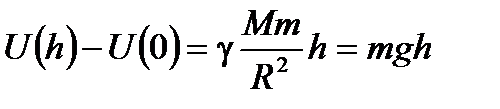 .
.
Получаем
| mg |
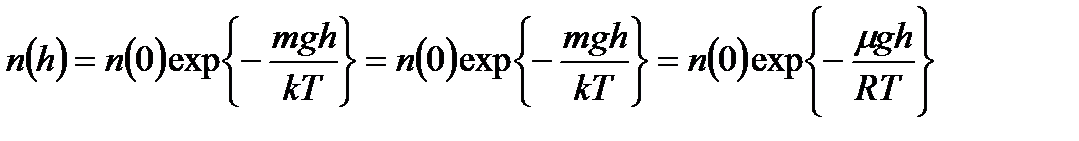 .
.
Здесь m - молярная масса газа, R - универсальная газовая постоянная. Воспользовавшись связью между концентрацией и давлением, получаем барометрическую формулу Больцмана
|
|
|
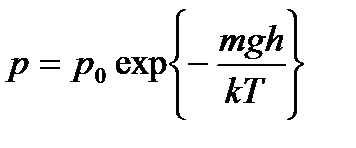 (2. 39)
(2. 39)
Концентрация частиц убывает с высотой, причем концентрация более тяжелых частиц убывает с высотой быстрее. Это создает подъемную силу для более легких объектов (воздушные шары). Для более высоких температур распределение с высотой становится более равномерным. При этом полное число частиц сосуде N постоянно и равно 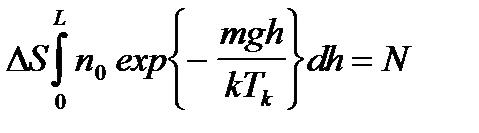 . Здесь DS площадь сечения сосуда, а L его полная высота;
. Здесь DS площадь сечения сосуда, а L его полная высота;
2) Распределение частиц во вращающемся сосуде. Имеем сосуд длины L, который вращается с угловой скоростью w вокруг одного из его оснований. Сила инерции, действующая на молекулу, находящуюся на расстоянии r от основания, равна  , а потенциальная энергия молекулы равна
, а потенциальная энергия молекулы равна 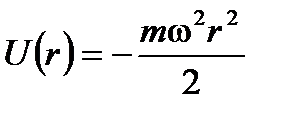 . Распределение частиц описывается функцией
. Распределение частиц описывается функцией 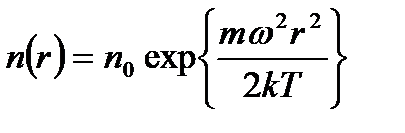 , которая показывает, что концентрация молекул растет с радиусом и достигает максимального значения у противоположного основания;
, которая показывает, что концентрация молекул растет с радиусом и достигает максимального значения у противоположного основания;
3) Средняя энергия, приходящаяся на колебательную степень свободы.
Распределение Максвелла-Больцмана (Гиббса) позволяет получить среднюю энергию, приходящуюся на колебательную степень свободы. Этим мы подтвердим теорему о равнораспределении энергии по степеням свободы и получим теплоемкость твердых тел при высоких температурах T (для которых применимо классическое описание).
Равновесное состояние кристалла - периодическое расположение атомов в пространстве. Однако, атомы не находятся в покое, а совершают малые тепловые колебания относительно положений равновесия. Пусть колебания совершаются вдоль оси 0x, тогда энергия такого осциллятора равна:
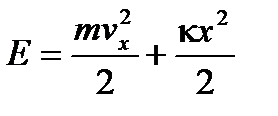 (2. 40)
(2. 40)
где m масса атома, 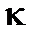 упругая постоянная. Статистическое описание атомов с энергией Е можно вести с помощью распределения Максвелла-Больцмана, которое для одного осциллятора имеет вид
упругая постоянная. Статистическое описание атомов с энергией Е можно вести с помощью распределения Максвелла-Больцмана, которое для одного осциллятора имеет вид
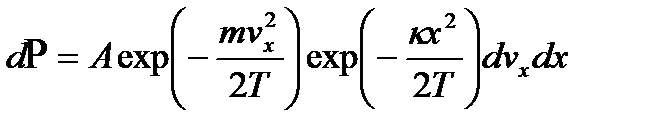 . (2. 41)
. (2. 41)
Во избежание путаницы здесь и далее вместо kT в знаменателе стоит T. Нормировочная постоянная A состоит из произведения двух постоянных (А = А1А2 ), которые равны соответственно:
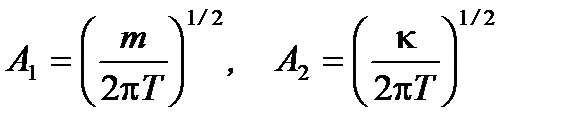 . (2. 42)
. (2. 42)
|
|
|
Найдем стандартным образом среднюю энергию тела, колеблющегося вдоль оси x:
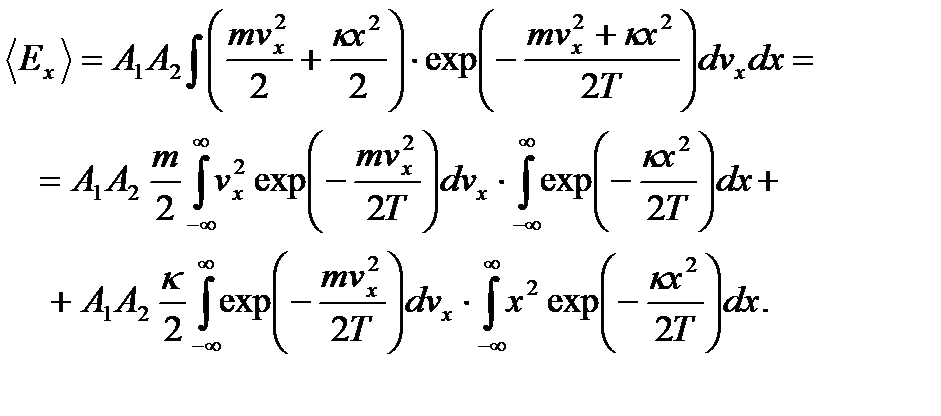
Второй интеграл в первом слагаемом есть по сути нормировочный интеграл и равен (А2)-1. То же относится к первому интегралу во втором слагаемом, который равен (А1)-1. Другие интегралы равны:
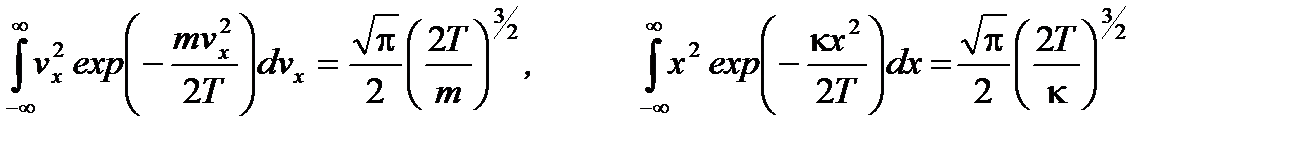 . (2. 43)
. (2. 43)
Подставляя (2. 43) в выражение для средней энергии, получаем
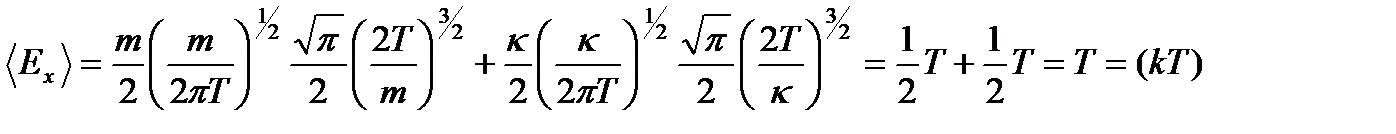 (2. 44)
(2. 44)
Итак, на одну колебательную степень свободы приходится энергия, равная в общепринятых единицах kT. Из расчета видно, что kТ/2 возникла из-за усреднения кинетической энергии колебательного движения, а kТ/2 - из-за потенциальной энергии колебательного движения. Здесь мы доказали теорему о равномерном распределении энергии по степеням свободы. Согласно этой теореме на каждую колебательную степень свободы приходится энергия, равная kТ.
|
|
|


