Флуктуации числа молекул в объеме.

Флуктуации числа молекул в объеме.

Ранее мы ввели дисперсию 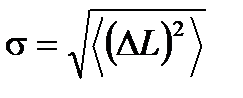 и относительную квадратичную флуктуацию , где N - число испытаний (число молекул). Рассмотрим флуктуации для биномиального распределения.

Среднее значение числа молекул 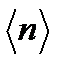 в объеме V₁ равно

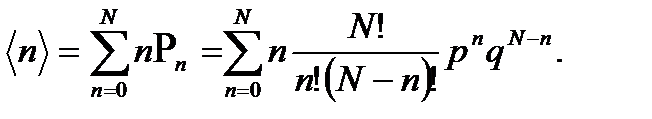                                 (1. 26)

Чтобы сосчитать данную сумму, воспользуемся красивым формальным приемом. Запишем среднее значение через производную:

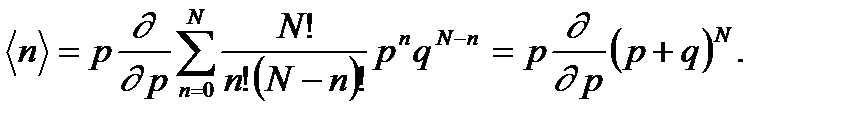                         (1. 27)

На самом деле p + q = 1, но такое значение подставлять сразу нельзя. Этим можно воспользоваться только после вычисления производной.

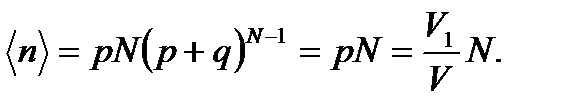                                         (1. 28)

Интересно отметить, что среднее значение совпадает с наиболее вероятным значением n, т. е. соответствует равномерному заполнению всего сосуда. Когда V₁ = V/2, получаем .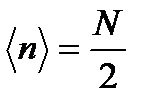

Относительная квадратичная флуктуация.

Чтобы сосчитать квадратичную флуктуацию (дисперсию) необходимо знать 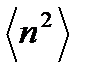. Вычислим 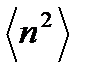аналогично тому, как это делалось в предыдущем пункте:

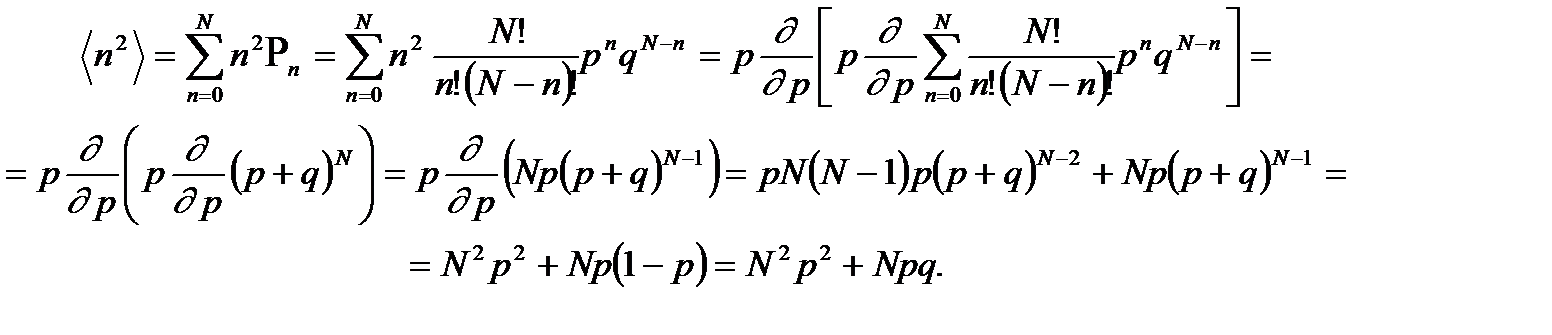
Здесь мы воспользовались тем, что p + q = 1. Итак,

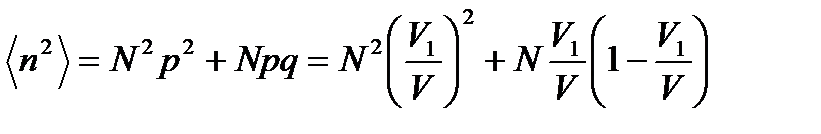.                           (1. 29)

Сосчитаем теперь относительную квадратичную флуктуацию. Сначала запишем дисперсию, которая равна

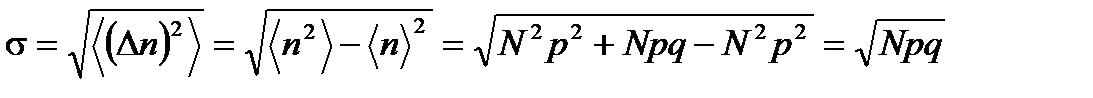,                (1. 30)

и тогда для относительной квадратичной флуктуации получаем

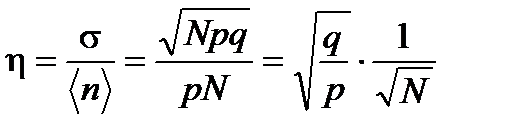.                                                   (1. 31)

Важно, что относительная квадратичная флуктуация убывает с ростом числа частиц в системе 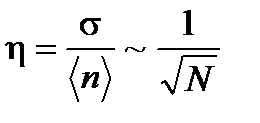. Физическое содержание полученного выражения очень важно. Исследуем его. Подставим в относительную квадратичную флуктуацию выражения для p и q из (1. 22):

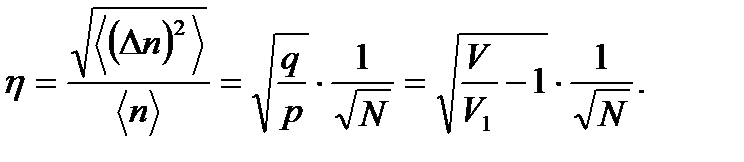                                      (1. 32)

Рассмотрим большой объем V₁ ® V, тогда относительная флуктуация стремится к нулю (h ® 0), т. к. число частиц в объеме V фиксировано.

При уменьшении объема V₁ (V₁ ® 0) относительная флуктуация возрастает, т. е. при V₁ < < V имеем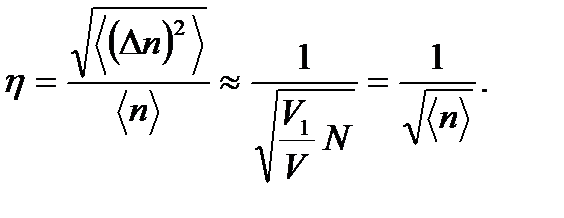                                   

Для 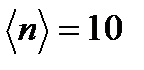 частиц в рассматриваемом объеме V₁ = V/2 относительная флуктуация равна .

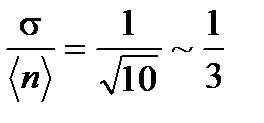 Для газа, находящегося в нормальных условиях, 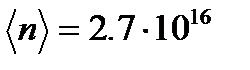 частиц/мм³. При V₁ < < V получаем очень малую величину относительной квадратичной флуктуации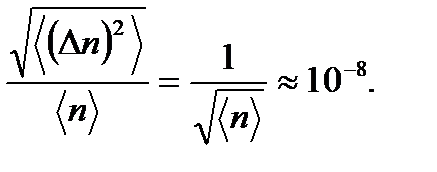

Итак, в макроскопических системах статистические флуктуации незначительны. С большой точностью все величины равны своим средним значениям. Иначе говоря, подавляющую часть времени газ находится в состояниях, в которых отклонения числа молекул от среднего не превышают относительную флуктуацию.

 

 

§1. 5. Статистическое распределение. Квазизамкнутость.

Рассмотрим систему с огромным числом частиц как реальное макроскопическое тело. При этом о такой системе говорят как о системе с большим числом степеней свободы.

Определение: числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы.

Положение материальной точки (частица, молекула) задается тремя координатами (x, y, z или r, q, j), следовательно, она имеет три степени свободы. Для сложных систем, состоящих из большого числа частиц, различают поступательные, вращательные и колебательные степени свободы.

Предположим, что система замкнутая, т. е. не взаимодействует ни с какими другими телами. Тогда состояние системы можно характеризовать энергией E, причем E = const. Но энергии отдельных кусочков системы могут не оставаться постоянными.

Итак, рассматриваем замкнутую макросистему с большим числом степеней свободы (частиц). Выделим из этой системы некоторую подсистему, весьма малую по сравнению со всей системой, но тоже имеющей большое число частиц (т. е. с большим числом степеней свободы). Подсистема является тоже макросистемой, но она уже не является замкнутой, она испытывает всевозможные внешние взаимодействия со стороны остальных частей системы.

Благодаря огромному числу степеней свободы остальных частей эти взаимодействия будут иметь весьма сложный и запутанный характер. Поэтому состояние рассматриваемой части системы будет меняться со временем также весьма сложным и запутанным образом. Точное решение проблемы о поведении такой системы является невыполнимой задачей. Необходим статистический подход описания поведения такой подсистемы. Он состоит в том, чтобы рассматривать различные состояния подсистемы как случайные величины, которые появляются в соответствии со своей вероятностью (как некоторое количество частиц в объеме V₁, рассмотренное ранее).

В самом деле, в силу сложности и запутанности внешних воздействий со стороны других частей системы, за достаточно долгий промежуток времени t выделенная нами подсистема пройдет через все возможные состояния. Вводя вероятность каждого состояния 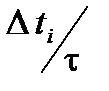 (где Dt_i - время нахождения в i-ом состоянии), мы получим какое-то распределение вероятностей, которое назовем статистическим распределением.

Статистическое распределение малой подсистемы не зависит:

1) от начального состояния какой-либо другой малой части той же системы, т. к. влияние этого начального состояния будет в течение времени t вытеснено влиянием остальных обширных частей макросистемы;

2) от начального состояния самой подсистемы, поскольку данная подсистема с течением времени проходит через все возможные состояния и каждое из них может быть выбрано в качестве начального.

Если статистическое распределение малой макроскопической подсистемы найдено, то можно вычислить вероятности различных значений любых величин, зависящих от состояния рассматриваемой подсистемы.

Выделенная подсистема незамкнута, она подвергается непрерывному воздействию со стороны прочих частей системы, именно благодаря этому и будет иметь место статистическое распределение. Однако энергия взаимодействия для достаточно большой макросистемы (с большим числом частиц) будет меньше энергии, содержащейся внутри подсистемы. Обмен внутренней энергией (тепловое взаимодействие) происходит через ограничивающую подсистему поверхность, т. е. во взаимодействии с окружающими частями участвуют преимущественно те частицы выделенной подсистемы, которые находятся вблизи поверхности. Обмен внутренней энергией - это поверхностный эффект. Наряду с этими взаимодействиями существуют взаимодействия отдельных частиц выделенной подсистемы друг с другом, которые являются уже объемным эффектом. С увеличением числа частиц в подсистеме объемные эффекты растут значительно быстрее, чем поверхностные, и при достаточно большом размере подсистемы ее взаимодействие с окружающими частями будет мало по сравнению с внутренними взаимодействиями.

Подобные подсистемы трактуются как квазизамкнутые системы, т. е. как системы, которые, по крайней мере, в течение малых промежутков времени Dt ведут себя приблизительно так же, как и замкнутые системы. Таким образом, в течение достаточно малого промежутка времени всякая макроскопическая система, являющаяся малой частью замкнутой макроскопической системы, ведет себя приблизительно как замкнутая система, т. е. является квазизамкнутой.

При этом практически все величины, представляющие физический интерес, становятся аддитивными. В частности, полная энергия системы представима в виде суммы , где e_i - энергия i-ой квазизамкнутой подсистемы. Это равенство приблизительное, но точность его выполнения тем больше, чем больше частиц в системе и подсистемах.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: