 |
Статистическое равновесие.. §1.6.Фазовое пространство. Функция распределения.
|
|
|
|
Статистическое равновесие.
Если замкнутая макросистема находится в состоянии, в котором для каждой ее части, также являющейся самой по себе макросистемой, физические величины с большой относительной точностью равны своим средним значениям, то рассматриваемая замкнутая система находится в состоянии статистического равновесия.
Если система наблюдается в течение достаточно большого промежутка времени, то подавляющую часть этого промежутка оно проводит в состоянии статистического равновесия.
Если в какой-то начальный момент времени система не находилась в состоянии статистического равновесия (например, искусственно была выведена из него внешними воздействиями, а потом снова стала замкнутой), то в дальнейшем она обязательно перейдет в состояние статистического равновесия. Промежуток времени перехода в статистическое равновесие называется временем релаксации.
§1. 6. Фазовое пространство. Функция распределения.
Рассмотрим идеальный газ (нет взаимодействия между молекулами). Полная энергия идеального газа есть сумма кинетических энергий отдельных молекул: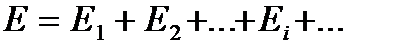 
, где 
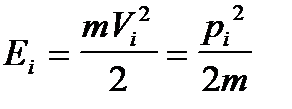. Поскольку молекулы не взаимодействуют, то каждая молекула может быть рассмотрена как квазизамкнутая подсистема. Обмен энергиями происходит при редких столкновениях молекул. Все молекулы обладают разными скоростями, даже в положении равновесия.
Подсистему (молекулу) будем характеризовать координатами и скоростями (или импульсами): x, y, z, px, py, pz. Таким образом, 6 величин задают положение частицы и ее состояние.
| x |
| z |
| y |
| · (x, y, z) |
| px(vx) |
| py(vy) |
| pz(vz) |
| · (px, py, pz) |
Рис. 1. 1. Координатное и импульсное фазовые пространства.
|
|
|
Введем понятие фазового пространства как пространства координат и импульсов (скоростей). Для подсистемы из одной молекулы это 6-ти мерное пространство. Различные состояния частицы можно изображать точками этого фазового пространства. С течением времени состояние частицы будет меняться, и тогда, соединяя все положения точек в различные моменты времени, получим фазовую линию в этом пространстве. Если система состоит из двух молекул, то их состояние задается 6+6 = 12 величинами, и мы имеем 12-ти мерное фазовое пространство.
Рассмотрим фазовое пространство в общем случае. Пусть рассматриваемая макросистема имеет n степеней свободы, т. е. положение точек этой системы в пространстве характеризуется n координатами, которые обозначим за qi (i=1, 2, 3,..., n). Состояние системы тогда определяется n координатами qi и n скоростями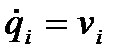 
(или импульсами pi). Введем фазовое пространство системы с числом измерений 2n. С течением времени состояние системы меняется и в фазовом пространстве, и это описывается фазовой линией.
Каждая система имеет свое фазовое пространство. Вероятность реализации различных состояний системы есть функция от координат и импульсов той системы. Координаты и импульсы в этом пространстве меняются непрерывном образом, а для непрерывных значений необходимо задавать элемент объема фазового пространства (как произведение координатной и импульсной частей объема):
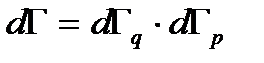(1. 33)
Это малая область пространства, куда может попасть система (поскольку точка не имеет измерения). Для одной частицы имеем
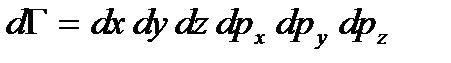. (1. 34)
Для n частиц
(1. 35)
Рассмотрим вероятность попадания системы в элемент этого фазового объема для идеального газа. Вероятность нахождения частицы в объеме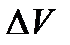 
известна: 
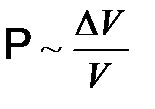, где 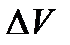- координатный кусок фазового пространства, 
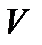- весь пространственный объем. В силу равной вероятности нахождения частицы в любой точке пространства можно записать 
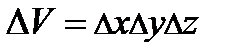. Причем в идеальном газе можно следить за состоянием 1 частицы в течение длительного времени (и определить 
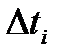в каждом i-ом состоянии) или следить сразу за
|
|
|
| DV=DGq |
| y |
| z |
| x |
| DGp |
| py |
| pz |
| px |
Рис. 1. 2. Элементы объёмов в координатном и импульсном фазовом пространстве.
всем коллективом и считать, сколько частиц попало в данный элемент фазового объема. Итак, для координатной части вероятность 
пропорциональна объёму (если нет внешнего поля). Для пространства импульсов энергия системы постоянна
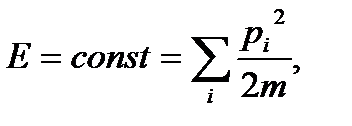(1. 36)
что вносит ограничение на элементы объема импульсов.
В общем случае элемент фазового объема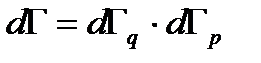 
, и тогда вероятность частицы попасть в этот элемент фазового объема можно записать
, (1. 37)
где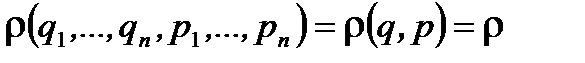 
- плотность вероятности (функции распределения) для системы иметь координаты и импульсы (скорости) в этом элементе объема. Запись (1. 37) для вероятности справедлива для любой квазизамкнутой системы.
Свойства функции распределения.
Рассмотрим основные свойства функции распределения. Во-первых, выполняется условие нормировки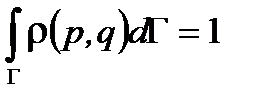 
, где интегрирование ведется по всему фазовому объему. Во-вторых, среднее значение физической величины 
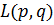определяется выражением
(1. 38)
Наконец, в-третьих, функция распределения обладает свойством стационарности. Рассматриваем подсистему в течение большого промежутка времени, который разобьем на большое число маленьких промежутков с моментами времени между ними t1, t2, t3,.... В эти моменты времени подсистема в фазовом пространстве изображается точкой. Количество этих точек в единице объема этого пространства (т. е. их плотность) будет пропорционально значению функции распределения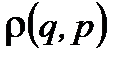 
.
Через момент времени Dt состояния всех одновременно рассматриваемых подсистем изменяется согласно уравнениям механики. Новые состояния подсистем (они совпадают с состояниями исходной подсистемы в моменты t1+Dt, t2+Dt,.... ) изобразятся в фазовом пространстве точками, которые с тем же правом, что и предыдущие, будут распределены с плотностью ~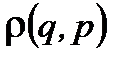 
. Логично предположить, что обе совокупности точек описываются одной и той же функцией распределения. Это свойство квазизамкнутых систем называется свойством стационарности статистического распределения. 
Имеет место теорема Лиувилля.
|
|
|
|
|
|
