 |
§1.8.Энтропия.
|
|
|
|
Флуктуации аддитивных величин. Итак, нам известно, что статистическое поведение и свойства замкнутой (квазизамкнутой) системы определяются аддитивными интегралами движения. Одним из наиболее важных свойств аддитивных величин является то, что их флуктуации в состоянии равновесия малы ( 
, где N число подсистем). Для доказательства разобьем квазизамкнутую подсистему на множество более мелких, квазизамкнутых одинаковых подсистем (каждая из них слабо взаимодействует с окружением). Пусть число таких подсистем N. Тогда энергия подсистемы равна сумме энергий более мелких подсистем: 
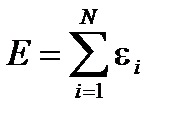. Для оценки средней энергии подсистемы можно считать, что средние энергии малых подсистем одинаковы, поскольку мы разбивали на мелкие одинаковые подсистемы. Тогда средняя энергия равна 
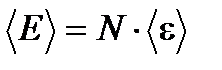. Сосчитаем среднюю квадратичную флуктуацию
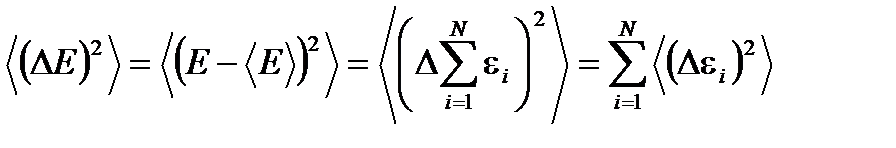(1. 46)
При выводе этой формулы мы воспользовались тем, что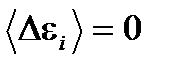 
. То, что формула справедлива, проще всего увидеть на примере двух малых подсистем с энергиями e1 и e2. В самом деле, для двух подсистем 
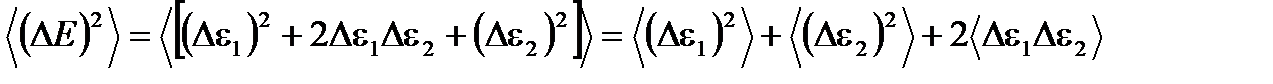. В силу квазинезависимости малых подсистем 
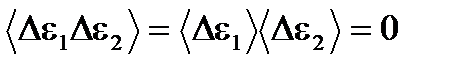, т. к. 
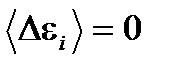. Поэтому 
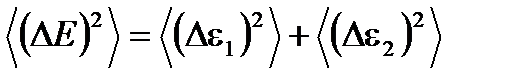. Аналогичный результат получается и для N малых подсистем. Воспользуемся еще раз тем, что малые подсистемы примерно одинаковы, и флуктуации в них в среднем также имеют одинаковые величины
(1. 47)
Тогда для относительной квадратичной флуктуации получаем:
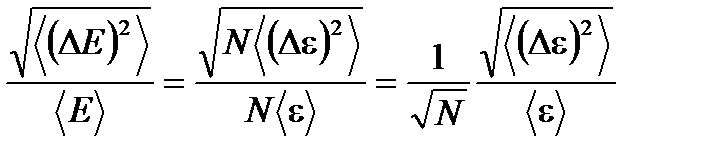(1. 48).
Как видно из этого соотношения, при больших значениях N относительные флуктуации ничтожно малы. Как и для распределения молекул по объему квазизамкнутая система живет подавляющую часть времени в состоянии с энергией близкой к средней энергии. Иначе, энергия равновесной подсистемы E практически постоянна во времени и равна своему среднему значению: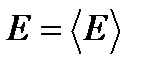 
. Это означает, что функция распределения имеет резкий пик при энергии 
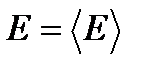и имеет качественную зависимость, изображенную на рисунке. Заметную величину 
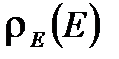имеет только при ничтожно малых отклонениях E от среднего значения 
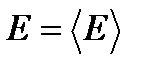. Итак, любая квазизамкнутая система почти все время проводит в очень небольшой части фазового пространства, соответствующей энергии вблизи 
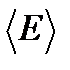. Эту область можно оценить, исходя из того, что площадь под кривой равна единице:
|
|
|
, (1. 49)
где 
высота области, а 
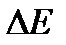ширина этой области (на полувысоте).
Статистический вес. По порядку величины 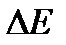(т. е. тот интервал энергий, в котором допустимы малые отклонения энергии подсистемы от своего среднего значения) совпадает со средней квадратичной флуктуацией 
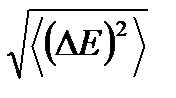. Поэтому для оценки разрешенной части фазового пространства, в которой рассматриваемая подсистема проводит подавляющую часть времени, можно в распределении по энергиям поставить среднее значение энергии. Тогда (1. 49) можно записать в виде
(1. 50)
Здесь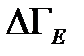 
- та разрешенная часть фазового пространства, в которой рассматриваемая подсистема со средней энергией 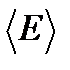проводит подавляющую часть времени. Объем 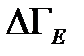несет информацию о полном числе микроскопических состояний подсистемы, которые реализуют макроскопическое состояние равновесной подсистемы с энергией .
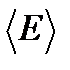Введем понятие статистического веса как числа микросостояний реализующих данное макросостояние. При статистическом описании тепловых свойств тел роль статистического веса играет фазовый объем 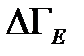. Этот объем тем больше, чем больше число микроскопических реализаций макроскопического состояния подсистемы с энергией 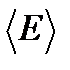. Однако, статистический вес, как он вводится по определению, есть величина безразмерная, а фазовый объем 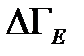- размерная величина. Поэтому определим статистический вес макроскопического состояния 
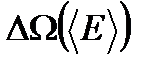как величину, пропорциональную фазовому объему 
:
|
|
|
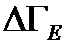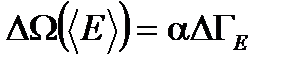(1. 51)
где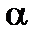 
- размерный коэффициент пропорциональности.
Если подсистему со средней энергией 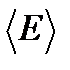разбить на подсистемы меньшего размера, то состояние каждой малой подсистемы будет определяться ее средней энергией. Для каждой маленькой подсистемы можно определить статистический вес 
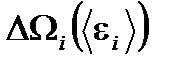ее макросостояния с энергией в интервале от 
до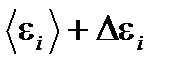 
. Так как маленькие подсистемы статистически независимы, то энергия рассматриваемой подсистемы 
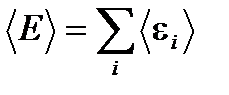, а её статистический вес по теореме об умножении вероятностей равен
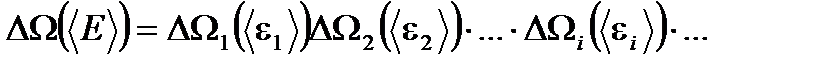(1. 52)
Энтропия. Удобнее вводить аддитивную величину, характеризующую макроскопическое состояние подсистемы (аддитивные величины обладают малыми флуктуациями). Энтропия подсистемы определяется соотношением
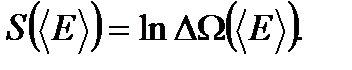(1. 53)
Энтропия дает информацию, как и статистический вес, о полном числе микросостояний подсистемы, которые реализуют данное равновесное состояние системы с энергией 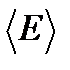. Термин энтропия на греческом языке означает “превращение”. Число микроскопических реализаций растет с увеличением степени беспорядка в подсистеме. Поэтому говорят, что энтропия является мерой степени беспорядка в подсистеме.
Из (1. 51) получаем
. (1. 54)
Энтропия большой подсистемы, статистический вес которой равен произведению статистических весов малых подсистем
,
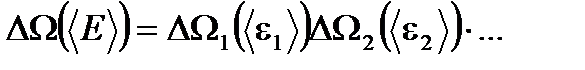равна сумме энтропий её малых равновесных частей
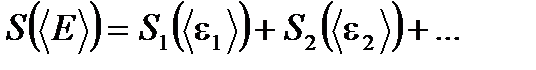(1. 55)
Энтропия - аддитивная величина. Следовательно, для энтропии флуктуации также малы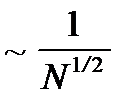 
. Из свойства аддитивности следует, что энтропия помимо энергии зависит от объема тела V, но не зависит от формы тела, т. к. изменение формы тела - это только перестановка его частей, соответствующая перестановке слагаемых в сумме энтропий отдельных малых подсистем. Таким образом, энтропия 
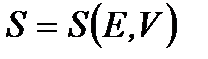, т. е. макроскопическое состояние определяется всего двумя параметрами: энергией тела E и его объемом V. Небольшое изменение макроскопического состояния тела сопровождается малым изменением энтропии dS, которое состоит из двух вкладов
|
|
|
. (1. 56)
Здесь первое слагаемое - приращение энтропии за счет изменения энергии тела, второе - за счет изменения объема тела. Во всех имеющихся в природе замкнутых системах энтропия никогда самопроизвольно не убывает, она увеличивается или остается постоянной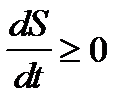 
. Закон возрастания энтропии устанавливает определенное направление течения процессов в природе.
|
|
|
