Краткие теоретические сведения

Основные формулы и уравнения

Состав газовой, смеси определяется количеством каждого из газов, входящих в смесь, и может быть задан мас­совыми или объемными долями.

Массовая доля определяется отношением массы отдель­ного газа, входящего в смесь, к массе всей смеси:

m₁ = M₁/M, m₂ = M₂/M, m₃ = M₃/M,………., m_n = M_n/M

где M₁, М_2,Мз,..., М_п — массы отдельных газов;

М - масса всей смеси.

Объемной долей газа называют отношение объема каждого компонента, входящего в смесь, к объему всей газовой смеси при условии, что объем каждого компонента отнесен к давлению и температуре смеси (приведенный объем):

r₁= V₁/V, r₂ = V₂/V, r₃ = V₃/V, ………….., r_n = V_n/V

где V₁, V₂, V₃,..., V_n - приведенные объемы компонен­тов газов, входящих в смесь;

V- общий объем газовой смеси.

Очевидно, что

M₁+M₂+M₃+……….+М_n = M

M₁+m₂+m₃+………..+m_n = 1

а также

V₁+V₂+V₃+………..+V_n = V;

r₁+r₂+r₃+…………..+r_n = 1

Для перевода массовых долей в объемные пользуются формулой

r_i = 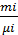∕ (24)

Объемные доли переводят в массовые по формуле

m_i = r_i*μ_i ∕ 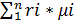(25)

Плотность смеси определяют из выражения

ρ_см = …… (26)

если известен массовый состав, по формуле

ρ_см = ……… (27)

Удельный объем смеси представляет величину, обратную ρ_см; поэтому, если дан объемный состав смеси, то

V_см = ….. (28)

 

Если же известен массовый состав, то

V_см = …. (29)

Из уравнения (26) легко получить значение так называемой кажущейся молекулярной массы газовой смеси

μ_см = 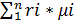…. (30)

или через массовый состав

μ_{см = …..} (31)

Газовую постоянную смеси газов (R_CM) можно выразить или через газовые постоянные отдельных компонентов, входящих в смесь, или через кажущуюся молекулярную массу смеси

Rсм = … (32)

или

R_см = 8314/μ_см = 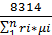… (33)

Связь между давлением газовой смеси и парциальными давлениями отдельных компонентов, входящих в смесь, устанавливается следующей зависимостью (закон Даль­тона), легко получаемой из основного уравнения кинети­ческой теории газов:

Р = Р₁+Р₂+Р_з+………+Р_n (34)

где- Р — общее давление газовой смеси;

P₁,Р₂,Р₃,……..Р_п — парциальные давления отдельных компонентов, входящих в смесь.

Парциальные давления определяются проще всего, если известны объемные доли отдельных компонентов, входящих в смесь;

Р₁ = Рr_1, P₂ = Pr₂ и т.д.

или вообще

P_i = Рr_i, (35)

где pi — парциальное давление любого газа, входящего в смесь.

Если известны массовые доли, то парциальное давле­ние любого газа, входящего в смесь,

P_i = m_i* R_i/R_см*Р (36)

В таблице 3 даны формулы для расчета газовых смесей.

 

Таблица 3 – Формулы для расчета газовых смесей

Задание состава смеси	Перевод из одного состава в другой	Плотность(кг/ м3) и удельный объем смеси(м3/кг)	Кажущаяся молекулярная масса смеси	Газовая постоянная смеси, (ДЖ/кг*К)	Парциальное давление, (Па)
Массовыми долями	ri= 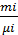∕	Vсм = ,   ρсм =	μсм =	Rсм=	Pi = mi* Ri/Rсм*Р
Объемными долями	mi = ri*μi ∕	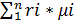r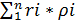см = ,   vсм =	μсм=	Rсм= =8314/μсм =	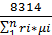Pi = Рri,

 

Теплоемкостью называют количество теплоты, которое необходимо сообщить телу (газу), чтобы повысить темпе­ратуру какой-либо количественной единицы на 1° С.

За единицу количества энергии в системе СИ приме­няют джоуль (Дж). В системе СИ джоуль является уни­версальной единицей, применяемой для измерения всех видов энергии: тепловой, механической, лучистой и пр. В качестве тепловой единицы 1 Дж представляет собой такое ее количество, которое появляется в результате превращения механической работы 1 Дж в теплоту. В качестве единицы механической энергии джоуль пред­ставляет собой работу, совершаемую силой, равной 1 нью­тону при перемещении ею тела на расстояние 1 м в направ­лении действия силы (1 Дж = Н*м = 1 кг *м²/с²).

В зависимости от выбранной количественной единицы вещества различают мольную теплоемкость μс — кДж/(кмоль*К), массовую теплоемкость с — кДж/(кг*К) и объемную теплоемкость с' — кДж/(м³*К).

Как было указано выше, 1 м³ газа в зависимости от параметров его состояния имеет разные массы. В связи с этим объемную теплоемкость всегда относят к массе газа, заключенной в 1м³ его при нормальных условиях [р_н = 101 325 Па (760 мм рт. ст.) и Т_н =273 К (t_н = 0°С).

Для определения значений перечисленных выше теплоемкостей достаточно знать величину одной какой-либо из них. Удобнее всего иметь величину мольной теплоем­кости. Тогда массовая теплоемкость

с = μс/μ (37)

а объемная теплоемкость

с' = μс/22,4 (38)

Объемная и массовая теплоемкости связаны между собой зависимостью

с' = сρ_н,

где ρ_н—плотность газа при нормальных условиях.

Теплоемкость газа зависит от его температуры. По тому признаку различают среднюю и истинную тепло­емкость.

Если q — количество теплоты, сообщаемой единице количества газа (или отнимаемого от него) при изменении температуры газа от t₁ до t₂ (или, что то же, от Т₁ до Т₂), то

с_т = q/t₂-t₁ (39)

представляет собой среднюю теплоемкость в пределах t₁—t₂. Предел этого отношения, когда разность темпера­тур стремится к нулю, называют истинной теплоем­костью. Аналитически последняя определяется как

c = dq /dt

Теплоемкость идеальных газов зависит не только от их температуры, но и от их атомности и характера процесса. Теплоемкость реальных газов зависит от их природных свойств, характера процесса, температуры и давления.

Для газов особо важное значение имеют следующие два случая нагревания (охлаждения):

1) изменение состояния при постоянном объеме;

2) изменение состояния при постоянном давлении/

Обоим этим случаям cоответствуют различные зна­чения теплоемкостей.

Таким образом, различают истинную и среднюю тепло­емкости:

а) мольную — при постоянном объеме (μс_v и μс_mv,) и постоянном давлении (μс_р и μс_рm);

б) массовую - при постоянном объеме (c_v и с_vm) и постоянном давлении (с_р с_рт);

в) объемную—при постоянном объеме (с'_v и с′_рт) и постоянном давлении (с'_р и с′_рт)

Между мольными теплоемкостями при постоянном давлении и постоянном объеме существует следующая зависимость:

μс_р - μс_v = μR = 8,314 кДж/(кмоль*К) (40)

Для приближенных расчетов при невысоких темпера­турах можно принимать следующие значения мольных теплоемкостей (таблица 4).

 

Таблица 4 - Приближенные значения мольных теплоемкостей при постоянном объеме и постоянном давлении (с = const)

Газы	Теплоемкость в кДж/(кмоль*К)
μср	μсv
Одноатомные Двухатомные Трех- и многоатомные	12,56 20,93 29,31	20,93 29,31 37,68

В технической термодинамике большое значение имеет отношение теплоемкостей при постоянном давлении и постоянном объеме, обозначаемое буквой k:

k = μс_р/ μс_v = с_р/с_v

Если принять теплоемкость величиной постоянной, то на основании данных таблицы 4 получаем: для одноатом­ных газов k = 1,67; для двухатомных газов k = 1,4; для трех- и многоатомных газов k =1,29.

Теплоемкость газов изменяется с изменением темпе­ратуры, причем эта зависимость имеет криволинейный характер. В таблицах V—XII (смотри приложения учебного пособия О.М. Рабинович «Сборник задач по технической термодинамике» М., «Машиностроение», 2011,344с) приведены теплоемкости для наиболее часто встречающихся в тепло­технических расчетах двух- и трехатомных газов.

При пользовании таблицами значения истинных тепло­емкостей, а также средних теплоемкостей в пределах от 0° до t берут непосредственно из этих таблиц, причем в не­обходимых случаях производится интерполирование.

Количество теплоты, которое необходимо затратить в процессе нагревания 1 кг газа в интервале температур от t₁ до t₂

q =(с_т)׀_t1^t2 (t₂ - t₁) = c_m2t₂ – c_m1t₁ (41)

где c_m1 и с_т2 — соответственно средние теплоемкости в пределах 0° — t₁ и 0° - t₂.

Из формулы (41) легко получить выражения для опре­деления количества теплоты, затрачиваемой в процессе при постоянном объеме и в процессе при постоянном давле­нии, т. е.

q_v = c_vm2t₂ – c_vm1t₁ (42)

q_p = c_pm2t₂ – c_pm1t₁ (43)

Если в процессе участвуют М кг или V_H м³ газа, то:

Q_v = М (c_vm2t₂ — c_vm1t₁) = V_н (cˊ_vm2t₂ — c'_vm1t₁); (44)

Q_p = М (c_pm2t₂ — c_pm1t₁) = V_н (cˊ_pm2t₂ — c'_pm1t₁); (45)

Нелинейную зависимость истинной теплоемкости от температуры представляют обычно уравнением вида

с = a + bt+ dt²,

где а, b и d — величины, постоянные для данного газа.

Часто в теплотехнических расчетах нелинейную за­висимость теплоемкости от температуры заменяют близ­кой к ней линейной зависимостью. В этом случае истинная теплоемкость

с = а + bt,

а средняя теплоемкость при изменении температуры от t1 доt₂

c_m = a+ b/2+(t₁ + t₂),

где а и b — постоянные для данного газа.

Для средней теплоемкости в пределах 0° — t эта фор­мула принимает вид

c_m = a+b/2t (46)

В таблице 5 приведены интерполяционные формулы для истинных и средних мольных теплоемкостей при постоянном давлении, а в таблице 6 — для средних массовых объемных теплоемкостей при постоянном объеме.

 

Таблица 5 - Интерполяционные формулы для истинных и средних мольных теплоемкостей газов при постоянном давлении

Газ	Мольная теплоемкость при Р = const в Дж/(кмоль*К)
истинная	средняя
	В пределах 0 – 10000С
О2	µcp = 29,5802 + 0,0069706t	µcpm =29,2080 + 0,0040717 t
N2	µcp = 28,5372 +0,0053905 t	µcpm = 28,7340 + 0,0023488 t
CO	µcp = 28,7395 + 0,0058862 t	µcpm = 28,8563 + 0,0026608 t
Воздух	µcp = 287558 + 0,0057208 t	µcpm = 28,8270 + 0,0027080 t
Н2О	µcp = 32,8367 + 0,0116611 t	µcpm = 33,1494 + 0,0052749 t
SO2	µcp = 42,8728 + 0,0132043 t	µcpm = 40,4386 + 0,0099562 t
	В пределах 0 – 15000С
H2	µcp = 28,3446 + 0,0031518 t	µcpm = 28,7210 + 0,0012008 t
CO2	µcp = 41,3597 + 0,0144985 t	µcpm = 38,3955 + 0,0105838 t
	В пределах1000 – 27000С
О2	µcp = 33,8603 + 0,021951 t	µcpm = 31,5731 + 0,0017572 t
N2	µcp = 32,7466 + 0,016517 t	µcpm = 29,7815 + 0,0016835 t
CO	µcp = 33,6991 + 0,0013406 t	µcpm = 30,4242 + 0,0015579 t
Воздух	µcp = 32,9534 + 0,0017806 t	µcpm = 30,1533 + 0,0016973 t
Н2О	µcp = 40,2393 + 0,0059854 t	µcpm =34,5118 + 0,0045979 t
	В пределах1500 – 30000С
H2	µcp = 31,0079 + 0,0020243 t	µcpm = 28,6344 + 0,0014821 t
CO2	µcp = 56,8768 + 0,0021738 t	µcpm = 48,4534 + 0,0030032 t

 

Теплоемкость газовой смеси

массовая

c_см = 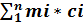… (47)

объемная

сˊ_см = 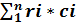.. (48)

мольная

 

mс_см = .. (49)

 

Таблица 6 - Интерполяционные формулы для средних массовых и объемных теплоемкостей газов при постоянном объеме

Газ	Теплоемкость в кДж/(кг*К)
массовая	объемная
	В пределах 0 – 10000С
О2	Cpm = 0,9127+0,00012724t	C΄pm = 1,3046+0,00018183t
	Cvm = 0,6527 +0,0001272t	C΄vm = 0,9337 + 0,00018183t
N2	Cpm = 1,0258 + 0,00008382 t	C΄pm = 1,2833 + 0,00010492 t
	Cvm= 0,7289 + 0,00008382 t	C΄vm = 0,9123 + 0,0000492 t
CO	Cpm = 1,0304 + 0,00009875 t	C΄pm = 1,2883 +0,00011966 t
	Cvm= 0,7335 + 0,00009575 t	C΄vm = 0,9173 + 0,00011966 t
Воздух	Cpm = 0,9952 + 0,00009349 t	C΄pm = 1,2870 + 0,00012091 t
	Cvm = 0,7084 + 0,00009349 t	C΄vm = 0,9161 + 0,00012091 t
Н2О	Cpm = 1,8401 + 0,00029278 t	C΄pm = 1,4800 + 0,00023551 t
	Cvm =1,3783 + 0,00029278 t	C΄vm = 1,1091 + 0,00023551 t
SO2	Cpm = 0,6314 + 0,00015541 t	C΄pm = 1,8472 + 0,00004547 t
	Cvm = 0,5016 + 0,00015541 t	C΄vm = 1,4763 + 0,00004547 t
	В пределах 0 – 15000С
Н2	Cpm = 14,2494 + 0,00059574 t	C΄pm = 1,2803 + 0,00005355 t
	Cvm = 10,1241 + 0,00059574 t	C΄vm = 0,9094 + 0,00005355 t
S2	Cpm = 0,8725 + 0,00024053 t	C΄pm = 1,7250 + 0,00004756 t
	Cvm = 0,6837 + 0,00024053 t	C΄vm = 1,3540 + 0,00004756 t

Примеры решения задач

1. Определить объемный состав воздуха, его газовую постоянную, кажущуюся молекулярную массу и пар­циальные давления кислорода и азота, если давление воздуха по барометру В =101 325 Па.

Решение:

По уравнению (24) получаем

r_O2 = = = 0,21

 

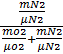r_N2 = = = 0,79

Газовую постоянную воздуха находим по уравне­нию (32)

R_см= = m_O2*R_O2 + m_N2*R_N2 = 0,232*260 + 0,768*295 = 287 Дж/(кг*К)

 

Кажущуюся молекулярную массу смеси определяем из уравнения (30)

μ_см = 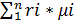= r_O2*μ_O2 + r_N2*μ_N2 = 0,21*32 + 0,79*28,02 = 28,9

или из уравнения (33)

R_см = 8314/μ_см

Отсюда

μ_см = 8314/Rсм = 8314/287 = 28,9

Парциальные давления получим из уравнения, (35)

P_i = Рr_i,

следовательно;

Р_О2 = r_O2*P = 0,21*101 325 = 21 278 Па;

Р_N2 = r_N2*P = 0,79*101 325 = 80 047 Па.

Ответ: r_O2 = 0,21, r_N2 = 0,79;

R_см = 287 Дж/(кг*К);

μ_см = 28,9;

Р_О2 = 21 278 Па;

Р_N2 =80 047 Па.

 

2.Смесь газов состоит из водорода и окиси углерода. Массовая доля водорода т_н, = 0,67%.

Найти газовую постоянную смеси и ее удельный объем при нормальных условиях.

Решение:

Из уравнения (32)

Rсм = = m₁*R₁ + m₂*R₂ = 0,0667*4124 + 0,9333*296,8 = 552 Дж/(кг*К).

Удельный объем газовой смеси получим из характериcтического уравнения

v_н = RT_н/Р_н = 552*273/ 101325 = 1,49 м³/кг.

Ответ: Rсм = 552 Дж/(кг*К); v_н = 1,49 м³/кг.

 

3.Найти объемную теплоемкость кислорода при по­стоянном объеме и постоянном давлении, считая с = const.

Решение:

По таблице 4 для двухатомных газов

mс_v = 20,93 кДж/(кмоль*К);

mс_p= 29,31 кДж/(кмоль*К).

Следовательно, для кислорода (и любого двухатомного газа)

сˊ_v = mс_v/22,4 = 20,93/22,4 = 0,934 кДж/(м³*К)

сˊ_р = m сˊ_р /22,4 = 29,31/22,4 = 1,308 кДж/(м³*К).

 

4. Вычислить среднюю массовую и среднюю объемную теплоемкость окиси углерода при постоянном объеме для интервала температур 0—1200° С, если известно, что для окиси углерода (mс_рm)¹²⁰⁰ = 32,192 кДж/(кмоль*К).

Сопоставить полученные результаты с данными таблицы VII. (смотри приложения учебного пособия О.М. Рабинович «Сборник задач по технической термодинамике» М., «Машиностроение», 2011,344с)

Р е ше н и е:

На основании формул (37), (38) и (40) имеем

(mс_рm)¹²⁰⁰ = 32,192 — 8,314 = 23,877 кДж(кмоль.*К);

(c_vm)¹²⁰⁰= (mc_v)¹²⁰⁰ /28 = 23,877/28 = 0,8528 кДж/(кг*К);

(cˊ_vm)¹²⁰⁰ = (mc_v)¹²⁰⁰/22,4 = 23,877/22,4 = 1,0659 кДж/(м3*К)

Из таблицы VII

(c_vm)¹²⁰⁰ = 0,8566 кДж/(кг*К); (cˊ_vm)¹²⁰⁰ = 1,0651кДж/(м^3*.К).

Ответ: (c_vm)¹²⁰⁰ = 0,8566 кДж/(кг*К); (cˊ_vm)¹²⁰⁰ = 1,0651кДж/(м^3*.К).

5.Вычислить среднюю теплоемкость с_рт для воздуха при постоянном давлении в пределах 200—800° С, считая зависимость теплоемкости от температуры нелинейной.

Решение:

По уравнениям (39) и (43)

(с_рm)^t2_t1 = с_рm2t₂ - с_рm1t₁/t₂ – t₁

Пользуясь таблицей XII, получим для воздуха

(с_рm)⁸⁰⁰=1,0710 кДж/(кг*К);

(с_рm)²⁰⁰= 1,0115 кДжДкг*К),

отсюда

(с_рm)⁸⁰⁰₂₀₀ =1,0710*800— 1,0115*200/800-200 = 1,091 кДж/(кг*К).

Ответ: (с_рm)⁸⁰⁰₂₀₀ = 1,091 кДж/(кг*К).

6.В закрытом сосуде объемом V = 300 л находится воздух при давлении р₁ = 0,8 МПа и температуре t₁= 20° С.

Какое количество теплоты необходимо подвести для того, чтобы температура воздуха поднялась до t₂ = 120°С? Задачу решить, принимая теплоемкость воздуха постоянной, а также учитывая зависимость теплоемкости от тем­пературы. Определить относительную ошибку, получае­мую в первом случае.

Ре ш е н и е:

Пользуясь уравнением состояния, определяем массу воздуха, находящегося в сосуде:

M= Vp/RT = 0,3*10⁶*0,3 / 287*293 = 1,07 кг

Для двухатомных газов, считая теплоемкость величи­ной постоянной, имеем

mс_v = 20,93 кДж/(кмоль*К);

следовательно, теплоемкость воздуха

с_v=mс_v /m = 20,93/28,96 = 0,7226 кДж/(кг * К)

Количество подведенной теплоты

Q = Mc_v (t₂-t₁) = 1,07*0,7227.100 = 77,3 кДж.

Теплоемкость воздуха с учетом ее зависимости от тем­пературы определяем из таблицы XII(смотри приложения учебного пособия О.М. Рабинович «Сборник задач по технической термодинамике» М., «Машиностроение», 2011,344с)

Пользуясь интерполя­цией, находим

с_v = 0,7209 кДж/(кг*К).

Следовательно, относительная ошибка

0,7227 - 0,7209/0,7209 *100% = 0,25%

Незначительная величина ошибки объясняется малым интервалом температур. При большой разности темпера­тур относительная ошибка может достигнуть весьма боль­шой величины.

Ответ: Q = 77,3 кДж

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: