 |
Лекция 1: введение в экономико-математические методы и модели. Балансовые модели. Модель леонтьева многоотраслевой экономики. Продуктивные модели.
|
|
|
|
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Владимирский государственный университет
Имени Александра Григорьевича и Николая Григорьевича Столетовых»
(ВлГУ)
Институт малого и среднего бизнеса
Кафедра «Коммерция и гостеприимство»
Мархайчук Мария Михайловна
Экономико-математические методы в торговле
Конспект лекций
по дисциплине «Экономико-математические методы в торговле» для студентов ВлГУ,
обучающихся по направлению 38.03.06 «Торговое дело»
Владимир – 2016 г.
ОГЛАВЛЕНИЕ
| ВВЕДЕНИЕ | ||
| ЛЕКЦИЯ 1. | Введение в экономико-математические методы и модели. Балансовые модели. Модель Леонтьева многоотраслевой экономики. Продуктивные модели | |
| ЛЕКЦИЯ 2. | Задачи математического и линейного программирования. Модели линейного программирования | |
| ЛЕКЦИЯ 3. | Геометрический метод решения задач линейного программирования | |
| ЛЕКЦИЯ 4. | Симплекс-метод для решения задач линейного программирования. | |
| ЛЕКЦИЯ 5. | Симплекс-таблицы для решения задач линейного программирования. Метод искусственного базиса. | |
| ЛЕКЦИЯ 6. | Взаимно двойственные ЗЛП. Первая и вторая теоремы двойственности | |
| ЛЕКЦИЯ 7. | Транспортная задача. Распределительный метод. | |
| ЛЕКЦИЯ 8. | Модели целочисленного ЛП. Метод Гомори | |
| ЛЕКЦИЯ 9. | Производственные функции. Основные характеристики и типы производственных функций | |
| ЗАКЛЮЧЕНИЕ | ||
| СПИСОК ЛИТЕРАТУРЫ |
ВВЕДЕНИЕ
Цель преподавания лекционного курса – дать студентам научное представление о методах, моделях и приемах, позволяющих получать количественные выражения закономерностей экономической теории на базе экономической статистики с использованием математико-статистического инструментария.
|
|
|
Современные социально-экономические процессы и явления зависят от большого количества факторов, их определяющих. В связи с этим квалифицированному специалисту необходимо не только иметь четкие представления об основных направлениях развития экономики, но и уметь учитывать сложное взаимосвязанное многообразие факторов, оказывающих существенное влияние на изучаемый процесс.
Такие исследования не возможно проводить без знания основ теории вероятностей, математической статистики, т.е. дисциплин, позволяющих исследователю разобраться в огромном количестве стохастической информации и среди множества различных вероятностных моделей выбрать единственную, наилучшим образом отражающую изучаемый процесс или явление.
В рамках курса эконометрики студенты получают и углубляют следующие знания:
− математической статистики, определяющей генеральную и выборочную совокупность, вариационные ряды и их характеристики; методы статистического оценивания параметров и статистической проверки гипотез (статистические критерии);
− методы корреляционно-регрессионного анализа для исследования взаимосвязи между зависимой переменной и группой влияющих на нее показателей;
− многомерных статистических методов, позволяющих выделять латентные факторы, сжимать признаковое пространство и сопоставлять изучаемые процессы в пространстве латентных факторов, проводить многомерную классификацию;
− владеть приемами статистического анализа нечисловой информации.
Задачами курса являются
1. Научиться строить экономические модели и оценивать их параметры;
2. Научиться проверять гипотезы о свойствах экономических показателей и формах их связи.
|
|
|
3. Иметь представление о программном обеспечении, основанном на эконометрических принципах.
В курсе описываются формы и типы классических эконометрических моделей, соотношения между ними, их достоинства и недостатки. Рассматриваются предпосылки построения моделей, а также задачи их спецификации и идентификации.
Курс рассчитан на 18 часов лекционного курса итоговый контроль знаний студентов проверяется в рамках текущего контроля.
Лекция 1: ВВЕДЕНИЕ В ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ. БАЛАНСОВЫЕ МОДЕЛИ. МОДЕЛЬ ЛЕОНТЬЕВА МНОГООТРАСЛЕВОЙ ЭКОНОМИКИ. ПРОДУКТИВНЫЕ МОДЕЛИ.
1. Понятие модели, ее классификация.
2. Балансовая модель.
3.Модель В. Леонтьева.
4. Продуктивные модели.
Термин «модель» используется в различных сферах человеческой деятельности и имеет множество смысловых значений. В нашем курсе лекций определим модель как материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале.
Следовательно, модель является инструментом научного познания. Она строится субъектом исследования так, чтобы отобразить характеристики объекта-оригинала (свойства, взаимосвязи, структурные и функциональные параметры и т.п.), существенные для цели исследования. Поэтому вопрос об адекватности модели объекту-оригиналу правомерно решать лишь относительно определенной цели.
Процесс построения, изучения и применения моделей называется моделированием. Моделирование в экономике – это воспроизведение экономических объектов и процессов в ограниченных, малых, экспериментальных формах, в искусственно созданных условиях.
В экономике в основном используется математическое моделирование посредством описания экономических процессов математическими зависимостями. При изучении экономических процессов математические модели рассматриваются в тесной связи с целевыми системами и представляют собой некоторые целостные структуры, называемые экономико-математическими моделями (ЭММ). Таким образом, ЭММ – модели, включающие в себя совокупность математических зависимостей, логических построений, схем, графиков и т.д., связанных в некоторую единую систему, имеющую экономический смысл.
|
|
|
Приведем следующую общую классификацию ЭММ.
По целевому назначению ЭММ делятся на теоретико-аналитические и прикладные. Теоретико-аналитические ЭММ предназначены для исследования общих свойств и закономерностей экономических процессов. Прикладные ЭММ используются при решении конкретных экономических задач.
По характеру отражения причинно-следственных связей выделяют жестко детерминистские ЭММ и ЭММ, учитывающие случайность и неопределенность.
По способам отражения фактора времени ЭММ делятся на статические и динамические. В статических ЭММ все зависимости относятся к одному моменту или периоду времени. Динамические ЭММ характеризуют изменения экономических процессов во времени.
По исследуемым экономическим процессам различают макроэкономические и микроэкономические ЭММ. Макроэкономические модели строятся на уровне национального хозяйства, а микроэкономические – на уровне организаций, их объединений и отдельных регионов.
Существуют и другие признаки классификации ЭММ. Причем с развитием экономико-математических исследований классификация исследуемых ЭММ расширяется.
Отметим также, что по характеру используемого математического аппарата при построении ЭММ различают методы классической и прикладной математики.
Методы классической математики включают математический анализ, линейную алгебру, теорию вероятностей и др.
Методы прикладной математики включают линейное, нелинейное, динамическое, целочисленное и другое программирование, математическую статистику, комбинаторику, теорию игр, управление запасами, теорию массового обслуживания, экспертные оценки и др.
Одним из признаков качества функционирования оргсистемы является критерий оптимальности ее функционирования. В сфере принятия экономических решений критерий оптимальности – это показатель, выражающий предельную меру экономического эффекта принимаемого управленческого решения для сравнительной оценки возможных решений и выбора наилучшего из них.
|
|
|
Критерий оптимальности, как правило, носит количественный характер. Например, в его роли могут выступить максимум прибыли или минимум затрат.
Математической формой критерия оптимальности в ЭММ является так называемая целевая функция, экстремальное значение которой характеризует предельно допустимую эффективность деятельности моделируемого объекта-оригинала.
На практике нередко успех операции оценивается не по одному, а сразу по нескольким критериям. В этом случае для выбора оптимального решения используют два подхода.
Первый подход заключается в том, что в целевой функции устанавливают приоритет критериев введением специальных коэффициентов (весов).
Второй подход состоит в отбрасывании из множества допустимых решений заведомо неудачных решений, уступающих другим по всем критериям. В результате такой процедуры остаются эффективные или так называемые «паретовские» решения, множество которых существенно меньше исходного.
Компромиссное решение – решение, оптимальное по всем критериям, как правило, не существует. И потому окончательный выбор приемлемого по этим критериям решения остается за лицом, принимающим решение.
В экономике существует баланс между отдельными отраслями. Рассмотрим простой вариант модели межотраслевого баланса – модель «затраты-выпуск».
Пусть имеется n различных отраслей, каждая из которых производит свой продукт и нуждается в продукции других отраслей (производственное потребление). Введем следующие обозначения:
xi ‑ общий объем продукции отрасли i за плановый год ‑ так называемый валовой выпуск отрасли i;
xij ‑ объем продукции отрасли i, расходуемый отраслью j в процессе производства;
yi ‑ объем продукции отрасли i, предназначенный к потреблению в непроизводственной сфере ‑ объем конечного потребления. В него входят создаваемые в хозяйстве запасы, личное потребление граждан, обеспечение общественных потребностей (просвещение, наука, здравоохранение, развитие инфраструктуры и т.д.), поставки на экспорт.
Указанные величины сведем в таблицу.
| Производственное потребление | Конечное потребление | Валовой выпуск |
| 
| 
|
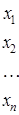
Балансовый характер этой таблицы выражается в том, что при любом 
выполняется соотношение
, (1.1)
означающее, что валовойвыпуск xi расходуется на производственное потребление, равное 
, и непроизводственное потребление, равное уi. Соотношения (1.1) называют соотношениями баланса.
Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки и т. п.), или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевой балансы. В дальнейшем будем иметь в виду стоимостной баланс.
|
|
|
В. Леонтьев обратил внимание на важное обстоятельство: величины 
остаются постоянными в течение ряда лет, что объясняется примерным постоянством используемой технологии производства.
Сделаем следующее допущение: для выпуска любого объема xj продукции отрасли j необходимо затратить продукцию отрасли i в количестве 
, т.е. материальные издержки пропорциональны объему производимой продукции:
. (1.2)
Коэффициенты 
называют коэффициентами прямых материальных затрат или коэффициентами материалоемкости. Они показывают сколько необходимо единиц продукции отрасли i для производства единицы продукции отрасли j, если учитывать только прямые затраты.
Подставив (1.2) в балансовое соотношения (1.1), получим
или, в матричной записи,
, (1.3)
где
Вектор 
называется вектором валового выпуска, вектор 
‑ вектором конечного потребления, а матрица А ‑ матрицей прямых затрат. Соотношение (1.3) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов 
и это соотношение называют также моделью Леонтьева.
Уравнения межотраслевого баланса можно использовать для плановых расчетов:
- задавая для каждой отрасли i валовой выпуск продукции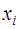 
можно определить объемы конечного потребления каждой отрасли 
:
,
где Е – единичная матрица;
- задавая величины конечного потребления каждой отрасли можно определить величины валового выпуска продукции :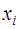
,
где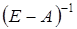 
– матрица, обратная к матрице 
, ее элементы называют коэффициентами полных материальных затрат.
Отметим особенности системы (1.3): все компоненты матрицы А, а также векторов и неотрицательны (это вытекает из экономического смысла А, и ). Для краткости будем записывать это так: 
.
Таким образом, плановые расчеты по модели Леонтьева можно выполнять при соблюдении следующего условия продуктивности:
матрица 
называется продуктивной, если для любого вектора 
существует решение 
уравнения (1.3).
В этом случае и модель Леонтьева, определяемая матрицей А, тоже называется продуктивной.
Сформулируем критерии продуктивности матрицы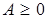 
.
Критерий I. Матрица продуктивна тогда и только тогда, когда матрица 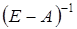существует и неотрицательна.
Критерий II. Матрица продуктивна тогда и только тогда, когда имеет место разложение матрицы 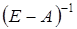в матричный ряд
. (1.4)
В соотношении (1.4) матрицы 
называются матрицами коэффициентов косвенных затрат 2-го, 3-го и т.д. порядков. Их сумма образует матрицу коэффициентов косвенных затрат
. (1.5)
Суть косвенных затрат поясним на примере производства двигателей. На их изготовление в виде прямых затрат расходуется сталь, чугун и т.д. Но для производства стали также нужен чугун. Следовательно, производство двигателей включает как прямые, так и косвенные затраты чугуна.
Таким образом, из соотношений (1.4) и (1.5) имеем
, (1.6)
т.е. матрица коэффициентов полных материальных затрат включает в себя матрицы коэффициентов прямых и косвенных затрат.
Рассмотрим примеры.
Пример 1. Исследовать на продуктивность матрицу
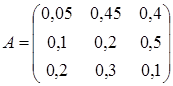
Решение. Сначала найдем матрицу 
:
Затем найдем 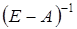. С этой целью по известным из линейной алгебры правилам вычислим определитель
алгебраические дополнения для элементов матрицы
; 
;
; 
;
; 
;
; 
;
.
Тогда
Полученная матрица неотрицательна и по Критерию I исходная матрица А продуктивная.
Пример 2. Для матрицы А коэффициентов прямых затрат из примера 1 и вектора конечного потребления
найти: а) вектор валового выпуска; б) матрицу косвенных затрат; в) изменение вектора валового выпуска при увеличении вектора конечного потребления на величину
Решение.
а) Вектор валового выпуска вычислим по формуле
.
Имеем
б) Матрицу косвенных затрат В найдем из соотношения (1.6):
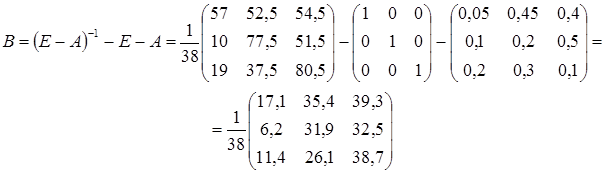
в)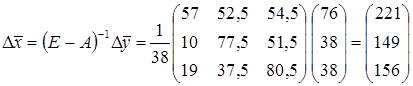 
Таким образом, при увеличении вектора конечного потребления на вектор валового выпуска увеличится на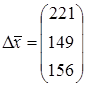 
.
|
|
|
