 |
Лекция 6: взаимно двойственные ЗЛП. Первая и вторая теоремы двойственности.
|
|
|
|
1. Взаимно двойственные задачи линейного программирования.
2. Первая теорема двойственности.
3.Вторая теорема двойственности.
С каждой ЗЛП связана двойственная к ней задача. Из решения одной задачи находят решение другой.
Пара взаимно двойственных ЗЛП имеет следующий вид.
| Задача I (исходная) | Задача I¢ (двойственная) |
 (6.1)
 (6.2)
Найти 
при условиях (6.1), (6.2)
|  (6.1¢)
 (6.2¢)
Найти 
при условиях (6.1¢), (6.2¢)
|
Если ввести в рассмотрение матрицу
из коэффициентов при неизвестных в системе (6.1), а также матрицы-столбцы
, 
, 
, 
,
то получим другую (матричную) форму записи задач I и I¢:
| Задача I (исходная) | Задача I¢ (двойственная) |
 (6.1)
 (6.2)
при условиях (7.1), (7.2)
|  (6.1¢)
 (6.2¢)
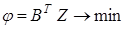при условиях (7.1¢), (7.2¢)
|
Задачи I и I¢ называются двойственными друг другу. Смысл, который вкладывается в это название, состоит в следующем.
1. Если первая задача имеет размеры 
(т ограничений с п неизвестными), то вторая ‑ размеры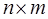 
.Так, в задаче I два ограничения с тремя неизвестными, а в задаче I¢ ‑ три ограничения с двумя неизвестными.
2. Матрицы из коэффициентов при неизвестных в левых частях ограничений обеих задач являются взаимно транспонированными. Так, в задаче I матрица из коэффициентов при 
, 
, 
есть A в то время как в задаче I¢матрица из коэффициентов при 
, 
есть 
.
3. В правых частях ограничений в каждой задаче стоят коэффициенты при неизвестных в целевой функции другой задачи.
4. В задаче I все ограничения представляют собой неравенства типа £, причем в этой задаче требуется достичь максимума f. Напротив, в задаче I¢ все ограничения суть неравенства типа ³, причем требуется достичь минимума j.
Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем двойственности.
|
|
|
Первая теорема двойственности. Если одна из взаимно двойственных задач (I) и (I¢) имеет оптимальное решение, то его имеет и другая, причем
.
Если в одной из задач (I) и (I¢) целевая функция не ограничена, то другая задача не имеет допустимых решений.
Вторая теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих неизвестных целевой функции исходной задачи, выраженной через свободные неизвестные ее оптимального решения.
Связь между первоначальными неизвестными одной из двойственных ЗЛП и дополнительными неизвестными другой задачи в общем виде устанавливается следующей таблицей.
| Переменные исходной задачи I | |
| Первоначальные | Дополнительные |
| 
|
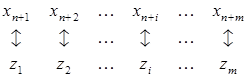
| Первоначальные | Дополнительные |
| Переменные исходной задачи I¢ |
Перейдем к примерам.
Пусть исходная задача – первая основная задача Лекции 3:
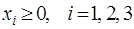
Тогда двойственная ей задача имеет вид
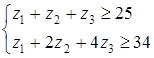
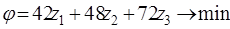
Решим ЗЛП М-методом.
Сначала введем балансовые переменные 
и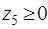 
, чтобы привести ЗЛП к каноническому виду, а затем и искусственные переменные 
и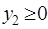 
. В результате получим следующую М-задачу
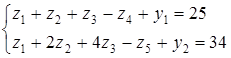
Составим первую симплекс-таблицу
| Базисные неизвестные | Свободные члены |
|
| 
| 
| 
| 
| 
|
|
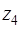
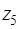
| –1 | |||||||
|
| 
| –1 | ||||||
| G |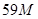 
| 
| 
| 
| 
|
| ||
|
| 
| 
| 
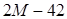
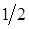
| –1 |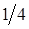 
| 
| ||
|
| 
|
|
|
|
| |||
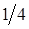
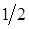
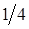
| G |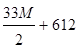 
| 
| 
|
| 
| 
| ||
|
| 
| 
| 
| 
| 
| |||
|
| 
|
|
|
|
| |||
| G | –32 | –10 | 
| 
| ||||
|
| –2 | –2 | –1 | |||||
|
| –1 | –1 | ||||||
| G | –12 | –36 | –6 | 
| 
|
В последней строке четвертой симплекс-таблицы нет положительных чисел (
достаточны большие) в столбцах неизвестных. Задача решена.
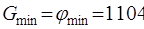
при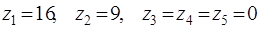 
.
Пользуясь теоремами двойственности нетрудно найти решение первой основной задачи.
|
|
|
Действительно, по первой теореме двойственности
.
Учитывая соотношения
по второй теореме двойственности из последней строки четвертой симплекс-таблицы имеем
т.е. 
– оптимальное решение первой основной задачи (ранее оно было получено в Лекциях 3 и 5).
Обратно, из последней строки симплекс-таблицы решение первой основной задачи легко находим решение двойственной задачи:
,
.
Экономический смысл рассмотренных взаимно двойственных ЗЛП.
Задача I об использовании ресурсов 
, 
и 
привела нас к плану выпуска продукции (36; 16), при котором прибыль от реализации продукции максимальная и составляет 1104 единиц.
Задачу I¢ можно трактовать следующим образом. Пусть на предприятии решили продать ресурсы , и вместо производства из него продукции 
, 
и 
.
Обозначим через
, 
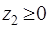и 
(6.1¢)
цена единиц ресурсов.
Справедливое требование к ценам со стороны продающего предприятия состоит в следующем: если взять ресурсы, идущие на изготовление единицы товара 
, то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать ресурсы – лучше изготовить из него товар и получить за него прибыль). Это требование приводит к неравенствам.
Других требований к ценам , и 
предприятие-продавец предъявлять не вправе. Что же касается покупателя, то для него единственное пожелание заключается в сокращении до минимума расходов на покупку ресурсов, т.е. величины
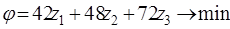
Решения взаимно двойственных ЗЛП (I) и (I¢) имеет следующий экономический смысл: предприятию безразлично, производить ли продукцию по оптимальному плану (36; 16) и получить максимальную прибыль 
единиц, либо продавать ресурсы по оптимальным ценам (16; 9; 0) и возместить от продажи равные ей минимальные затраты на ресурсы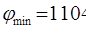 
единиц.
|
|
|
