 |
Лекция 3: геометрический метод решения задач линейного программирования
|
|
|
|
1. Понятие геометрического метода
2. Алгоритм решения задачи геометрическим методом.
Геометрический метод решения ЗЛП – простой и наглядный способ решения стандартных ЗЛП с двумя переменными:
(3.1)
при условиях
(3.2)
Рассмотрим следующие геометрические объекты.
Выпуклые множества и их свойства.
Множество точек называется выпуклым, если оно вместе с произвольными двумя своими точками содержит весь отрезок, соединяющий эти точки.
Например, четырехугольник 
на рис. 3.1 – выпуклое множество точек, а на рис. 3.2 выпуклым не является
Рис. 3.1 Рис. 3.2
Справедливо утверждение: пересечение любого числа выпуклых множеств есть выпуклое множество.
Каждое неравенство системы ограничений (3.2) геометрически определяет полуплоскость с граничной прямой 
, или 
, или 
.
Поясним сказанное. Рассмотрим, например, неравенство 
.
Посмотрим прямую L: 
(см. рис. 3.3).
Рис. 3.3
Для того чтобы определить, какая полуплоскость удовлетворяет заданному неравенству, необходимо выбрать любую точку, не лежащую на L, и подставить ее координаты в неравенство. Если неравенство будет выполняться, то данная точка является допустимым решением, и полуплоскость, содержащая точку, удовлетворяет неравенству. Как правило, в качестве «пробной» берут точку 
.
Подставим 
в заданное неравенство: 
. Получим истинное утверждение. Следовательно, заданному неравенству соответствует нижняя полуплоскость (заштрихованная на рис. 3.3), содержащая точку .
Полуплоскости, описываемые неравенствами (3.2) – выпуклые множества. Их пересечение – область допустимых решений ЗЛП, которая является также выпуклым множеством.
Это множество называют также многоугольником решений. Он может быть точкой, отрезком, лучом, ограниченным или неограниченным многоугольником. (Случай вырождения, когда система ограничений (3.2) – пустое множество и ЗЛП не имеет решения, исключается).
|
|
|
Ввиду неравенств 
и 
многоугольник решений всегда находится в первом квадранте координатной плоскости 
.
Для нахождения экстремума целевой функции F воспользуемся вектором набла 
- градиентом F:
.
Он показывает направление наискорейшего изменения целевой функции F.
Прямая 
называется линией уровня функции F. Иными словами на множестве всех точек 
линии уровня функции F она сохраняет постоянное значение 
.
Алгоритм решения ЗЛП геометрическим методом.
1. Строится многоугольник решений.
2. Строится вектор набла, перпендикулярно ему проводятся линии уровня и при этом учитывают, что оптимальное решение ЗЛП находится в угловой точке многоугольника решений.
3. Первая точка встречи линии уровня с многоугольником решений определяет минимум целевой функции (точка 
на рис. 3.5 и 3.6).
4. Последняя точка встречи линии уровня с многоугольником решений определяет максимум целевой функции (точка 
на рис. 3.5).
5. Если линия уровня параллельна одной из сторон многоугольника решений (сторона 
на рис. 3.6), то экстремум достигается во всех точках этой стороны . ЗЛП в этом случае имеет бесконечное множество решений.
Рис. 3.5 Рис. 3.6
6. Для нахождения координаты точки экстремума решают систему из двух уравнений прямых, дающих в пересечении эту точку.
По описанному алгоритму решим ЗЛП из предыдущей Лекции 2.
Пример 1. Экономико-математическая модель задачи о планировании производства.
Построим многоугольник решений. С этой целью запишем уравнения границ полуплоскостей из (3.7) в виде
или 
«Пробная» точка удовлетворяет всем неравенствам из (3.7) и потому многоугольник решений 
расположен в нижних полуплоскостях, порожденных прямыми 
, 
и 
как показано на рис. 3.7.
|
|
|
Построим вектор набла 
. Последней точкой встречи линии уровня с многоугольником решений будет точка (см. рис. 4.7) с координатами: 
, 
, являющимися решениями системы уравнений
Подставив координаты точки в целевую функцию, найдем
Рис. 3.7
Пример 2. Экономико-математическая модель задачи о диете.
Построим многоугольник решений. С этой целью запишем уравнения границ полуплоскостей в виде
или 
«Пробная» точка удовлетворяет всем неравенствам и потому многоугольник решений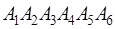 
расположен в верхних полуплоскостях, порожденных прямыми , и как показано на рис. 3.8.
Построим вектор набла 
. Первой точкой встречи линии уровня с многоугольником решений будет точка (см. рис. 3.8) с координатами: 
, 
, являющимися решениями системы уравнений:
Подставив координаты точки в целевую функцию, найдем
Рис. 3.8
|
|
|
