Лекция 7: транспортная задача. Распределительный метод.

1. Транспортная задача.

2. Алгоритм решения транспортной задачи.

3. Распределительный метод решения задачи.

Частным случаем ЗЛП является так называемая транспортная задача. Она состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления A ₁, A ₂, …, A _m в n пунктов назначения B ₁, B ₂, …, B _n.

При этом в качестве критерия оптимальности берут либо минимальную стоимость перевозок всего груза, либо минимальное время его доставки. Выберем минимальную стоимость перевозок. Примем обозначения: c _ij. –тарифы перевозки единицы груза из i -ого пункта отправления в j -ый пункт назначения; a _i – запасы груза в A _i; b _j – потребности в грузе в B _j; x _ij – количество груза перевозимого из A _i в B _j. Тогда математическая постановка транспортной задачи состоит в следующем:

(7.1)

при условиях

(7.2)

(7.3)

(7.4)

Транспортную задачу, как ЗЛП в канонической форме, решают распределительным методом, являющимся упрощенной модификацией симплекс-метода. Упрощение обусловлено специфичностью систем ограничений (7.2), (7.3) – неизвестные входят в них лишь по одному разу с коэффициентами, равными единице или нулю.

Исходные данные транспортной задачи записывают в виде таблицы 7.1.

Таблица 7.1

Пункты отправления	Пункты назначения	Запасы
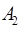
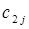
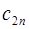
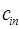
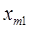
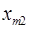
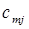
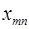
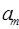
Потребности

 

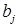
Всякое неотрицательное решение систем линейных уравнений (7.2), (7.3) определяемое матрицей 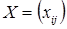размерности m ´ n называют планом транспортной задачи. План 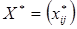, m ´ n называют оптимальным планом транспортной задачи (7.1) – (7.4), если функция (7.1) при этих значениях принимает минимальное значение.

Всюду ниже будем рассматривать закрытую модель транспортной задачи, т.е. случай, когда общая потребность в грузе пунктов назначения равна запасу грузов в пунктах отправления

(7.5)

Замечание. Если условие (7.5) не выполняется, то модель транспортной задачи называют открытой. Ее решение сводится к решению закрытой модели, путем введения фиктивных пунктов отправления или потребления с нулевыми тарифами.

Справедлива следующая теорема.

Теорема. Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось соотношение (7.5).

Решение транспортной задачи распределительным методом выполняют посредством шагов, на каждом из которых неизвестные разбиваются на базисные и свободные. Число базисных неизвестных транспортной задачи равно рангу системы линейных алгебраических уравнений (7.2), (7.3) и равно . Каждому разбиению неизвестных задачи на базисные и свободные соответствует базисное решение, заключающееся в заполнении таблицы поставок (базисном заполнении). Клетки заполненные базисными неизвестными, называют базисными, а клетки, соответствующие свободным неизвестным, – свободными.

Алгоритм решения транспортной задачи:

1. Находят первоначальное базисное распределение поставок – опорный план.

2. Проверяют опорный план на оптимальность.

3. Если решение оказалось неоптимальным, то переходят к следующему базисному распределению. Процесс повторяют до тех пор, пока базисное решение станет оптимальным.

Для нахождения опорного плана существуют разные методы. Укажем два из них – метод северо-западного угла и метод наименьших затрат на примере транспортной задачи, заданной следующей таблицей

Таблица 7.2

					Запасы
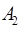
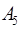
Потребности

Метод северо-западного угла или диагональный метод. При этом методе на каждом шаге построения опорного плана заполняется верхняя левая клетка («северо-западный угол») оставшейся части таблицы.

Заполняем клетку (1; 1): . В результате запасы груза в пункте израсходованы. Строка выпадает из последующего рассмотрения. Заполняем клетку (2; 1): 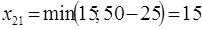. Запасы груза в пункте 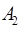также израсходованы и строка 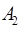выпадает из последующего рассмотрения. Заполняем клетку (3; 1): . В результате столбец выпадает из последующего рассмотрения: потребности в грузе пункта удовлетворены .

Заполняем клетку (3; 2): . Строка выпадает из последующего рассмотрения. Заполняем клетку (4; 2): . Строка выпадает из дальнейшего рассмотрения. Заполняем клетку (5; 2): . Столбец выпадает из последующего рассмотрения .

Заполняем клетку (5; 3). В ней запасы груза 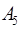в пункте и потребности в грузе в пункте также 25. Следовательно . Заполнение клеток завершено. Оно началось с левой верхней клетки (1; 1) и закончилось в клетке (5; 3), т.е. происходило по диагонали таблицы с севера на запад.

Получили опорный план в виде таблицы 7.3 с числом базисных клеток:

Таблица 7.3

 

Общая стоимость перевозок при таком опорном плане составляет: .

Недостаток метода северо-западного угла заключается в том, что опорный план построен без учета тарифов.

Метод минимальных затрат. На каждом шаге заполняют клетку с наименьшим тарифом. Применим этот метод к рассмотренной выше транспортной задаче.

Минимальный тариф, равный 2, находится сразу в нескольких клетках: (2; 3), (3; 2) и (4; 1). Выберем одну из них, например, (2; 3) и заполним ее: 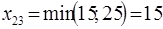. Исключаем из рассмотрения строку 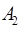и считаем потребности пункта равными единиц. В оставшейся части таблицы (строки , , и 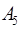, столбцы , и ) содержатся две клетки (3; 2) и (4; 1) с минимальным тарифом, равным 2. Выберем, к примеру, клетку (3; 2) и заполним ее: . Исключаем из рассмотрения строку и считаем потребности пункта равными единиц. В оставшейся части таблицы (строки , и 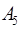и столбцы , , ) содержится лишь одна клетка (4; 1) с минимальным тарифом, равным 2. Заполним ее: . Повторяя предыдущие рассуждения, последовательно выберем и заполним следующие клетки:

(1; 2), ;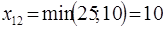

(5; 1), ;

(1; 1), ;

(1; 3), .

Получим опорный план в виде таблицы 7.4 с числом базисных клеток .

 

Таблица 7.4

 

Общая стоимость перевозок при таком опорном плане составляет: .

Очевидно, опорный план, полученный методом наименьших затрат предпочтительнее опорного плана, полученного методом северо-западного угла: 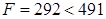. Но является ли он оптимальным? Ответ на этот вопрос дает следующая теорема (критерий оптимальности).

Сформулированный критерий оптимальности позволяет построить алгоритм решения транспортной задачи.

1. Находят опорный план (методом северо-западного угла или методом наименьших затрат). При этом число заполненных клеток должно быть .

2. Находит потенциал и пунктов отправления и назначения из системы уравнений

,

где – тарифы, стоящие в заполненных клетках таблицы 7.3 или 7.4.

Здесь следует иметь в виду, что число неизвестных 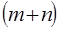, а число уравнений – . Следовательно, система уравнений имеет бесконечное число решений. Для однозначности решения один из потенциалов приравнивают к нулю (как правило ).

3. Для каждой свободной клетки определяют число , если среди чисел нет положительных, то получаем оптимальный план. Если же они имеются, то переходят к новому опорному плану.

4. Из всех чисел 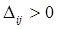выбирают максимальное и соответствующую ему свободную клетку, заполняют, пользуясь циклом. Циклом называют замкнутую ломанную линию, состоящую из горизонтальных и вертикальных отрезков прямых. одна из вершин находится в свободной клетке, а остальные – в занятых клетках, число вершин всегда четное, причем две соседние вершины расположены либо в одной строке, либо в одном столбце. Чаще всего ломанная имеет вид прямоугольника, но возможны иные фигуры (см. рис. 8.1).

Если ломаная линия, образуя цикл, пересекается, то точки самопересечения не являются вершинами. Для любой свободной клетки можно построить лишь один цикл. После того как он построен, следует перемещение грузов по следующим правилам:

- каждой из клеток, связанной циклом с данной свободной клеткой, приписывается определенный знак (в вершинах), причем свободной клетке «+», а всем остальным – поочередно «–» и «+» (плюсовые и минусовые клетки);

- в данную свободную клетку переносят меньшее из чисел x_ij, стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках и вычитают из чисел, стоящих в минусовых клетках. Клетка, бывшая свободной, становится занятой, а минусовая клетка, в которой стояло минимальное из чисел x_ij становится свободной.

Отметим, что если в минусовых клетках окажется два и более одинаковых числа x_ij, то освобождают лишь одну из них, а остальные оставляют занятыми с нулевыми поставками.

 

Рис. 7.1

5. Полученный опорный план проверяют на оптимальность, т.е. снова повторяют все действия, начиная с п. 2

Теорема. Опорный план транспортной задачи является оптимальным тогда и только тогда, когда ему соответствует система из 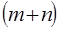чисел и удовлетворяющих условиям:

для занятых клеток,

для свободных клеток.

Числа и , сопоставляемые соответственно каждому пункту отправления и каждому пункту потребления, называют потенциалами пунктов отправления и назначения. В процессе решения составляют числа .

Применим описанный алгоритм к решению рассмотренной выше транспортной задачи.

п. 1. Найдем первый опорный план методом наименьших затрат (таблица 7.3).

п. 2. Найдем потенциалы и для занятых клеток. Составим систему уравнений.

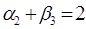
Полагая , найдем , , , , , , .

п. 3. Для свободных клеток составим числа :

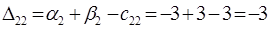
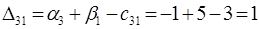
Построенный опорный план не является оптимальным, т.к. среди чисел есть положительные: и .

п. 4. Построим цикл для свободной клетки (3; 1) и припишем знаки каждой клетке в вершинах ломанной как показано в таблице 7.5.

 

 

Таблица 7.5

	–	+
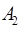
		+ 3	–

 

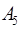
Выберем минимальное из чисел и , стоящих в минусовых клетках:

Переместим грузы в клетках, связанных циклом. Прибавим 5 к числам и , сторящих в плюсовых клетках, и вычтем 5 из чисел и , стоящих в минусовых клетках. В результате получим новый опорный план, представленный таблицей 8.6, для которого

Таблица 7.6

	+	–
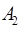
			– 2	+

 

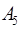
п. 5. Новый опорный план проверим на оптимальность, повторим предыдущие действия.

Имеем

, , , , , , , .

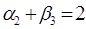
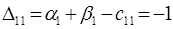
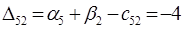
Построенный опорный план не является оптимальным .

Построим цикл для свободной клетки (3; 3) и припишем знаки каждой клетке, связанной с циклом как показано в таблице 7.6. Найдем 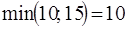, переместим грузы в соответствующих клетках и получим новый опорный план, представленный таблицей 7.7, для которого

 

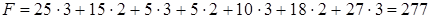
Таблица 7.7

 

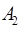
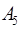
Проверим полученный опорный план на оптимальность.

Имеем

, , , , , , , .

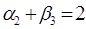
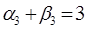
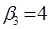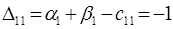
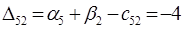
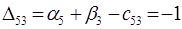
Среди чисел нет положительных. Полученный план оптимальный.

Ответ:

, .

Транспортная задача используется при решении и других экономических задач. Приведем примеры.

1. Задача оптимального использования оборудования.

Имеется m видов оборудования по изготовлению n типов деталей. Известно количество деталей каждого типа, изготавливаемых на каждом виде оборудования – , и необходимое количество требуемых деталей каждого типа – . Задается время использования i -го оборудования при изготовлении одной детали j -го типа – . Требуется определить минимальное время использования оборудования при выполнении планового задания. Математическая модель задачи имеет вид (8.1) – (8.4).

2. Задача оптимального распределения производства изделий на различных станках.

Имеется m различных станков, на которых может изготавливаться каждое из n изделий. Известны мощности станков – , в станко-часах и план выпуска изделий – , единиц. Задаются затраты в руб. на единицу j -го изделия при производстве его на i -ом станке – , а также производительность в шт/час i -го станка при производстве j -го изделия – . Требуется минимизировать суммарные затраты при выполнении плана выпуска. Математическая модель задачи имеет вид

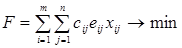
при условиях

,

,

.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: