 |
Лекция 8: модели целочисленного лп. Метод Гомори.
|
|
|
|
1. Модель целочисленного линейного программирования.
2. Метод Гомори.
Решения ряда ЗЛП, являющихся моделями экономических задач, должны выражаться в целых числах. Например, решения задач, в которых неизвестные означают число изготовленных изделий, число станков при загрузке оборудования и многое другое. Поэтому возникли ЗЛП, требующие целочисленного решения. Они формулируются при дополнительном ограничении: 
– целые числа.
Рассмотрим некоторые методы решения таких задач.
I. Пусть ЗЛП содержит две неизвестные и решение, найденное геометрическим методом, нецелочисленное. Тогда в области допустимых решений строят целочисленную решетку. На ней находят вершины с целочисленными координатами, в которых значение целевой функции наиболее близко к оптимальному нецелочисленному решению. Для этого перемещают линию уровня либо до первой точки встречи с построенной целочисленной решеткой в случае, когда ищется минимум целевой функции, либо до последней точки встречи – когда ищется максимум.
II. В случае если компоненты оптимального решения оказываются нецелочисленными, их округляют до ближайших целых чисел. Этот метод применяют тогда, когда отдельная единица совокупности составляет малую часть объема всей совокупности. В противном случае округление может привести к далекому от оптимального целочисленному решению. Поэтому используют специально разработанные методы. Один из них метод отсечения.
III.Метод отсечения или метод Гомори состоит в том, что сначала ЗЛП решается без условия целочисленности. Если полученное решение целочисленное, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, называемое отсечением.
|
|
|
Опишем его построение. Пусть в оптимальном решении задачи (
) компонента 
не является целой. Составим неравенство
, (8.1)
где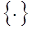 
– дробная часть числа.
Оно обладает свойствами правильного отсечения:
а) линейное относительно неизвестных 
,
б) отсекает найденный оптимальный нецелочисленный план,
в) не отсекает ни одного целочисленного решения.
Далее ЗЛП решается с учетом нового ограничения. Если полученное решение целочисленное, то задача решена. В противном случае добавляется новое ограничение и т.д.
Замечание. Если в оптимальном решении ЗЛП несколько нецелочисленных компонент, то из них выбирают компоненту с наибольшей целой частью.
Обратимся к примерам.
Задача. При модернизации оборудования в цехе выделено 72 м2 для установки оборудования первого и второго типов. На установку одного комплекта оборудования первого типа требуется 3 м2, на установку одного комплекта оборудования второго типа – 4 м2. Причем оборудование первого типа приносит ежемесячный доход 2 млн. руб., а оборудование второго типа – 6 млн. руб. Определить количество комплектов оборудования первого и второго типов, обеспечивающее максимальную прибыль, при условии, что предприятие может приобрести не более 16 комплектов оборудования первого типа и не более 8 комплектов оборудования второго типа.
Решение. Пусть – количество устанавливаемого оборудования j -го типа, 
. Тогда математическая модель задачи примет вид:
при условиях
,
где 
– целые числа.
Сначала решим задачу геометрическим методом.
На плоскости 
построим прямые:
или 
, 
и 
.
Очевидно, OABCD – многоугольник допустимых решений (см. рис. 8.1). Построим вектор 
. Перемещая линию уровня, убеждаемся, что точка B – последняя точка встречи линии уровня с многоугольником OABCD. Найдем координаты точки B:
, 
.
Таким образом, 
– нецелочисленное оптимальное решение ЗЛП.
|
|
|
Рис. 8.1
Для нахождения целочисленного решения ЗЛП методом I строим целочисленную решетку на плоскости и заменим многоугольник OABCD многоугольником OAKLMNPD (см. рис. 8.1). Его вершина K будет последней точкой встречи с линией уровня, т.е. координаты точки K: 
и оптимальное целочисленное решение ЗЛП.
Теперь найдем целочисленное решение методом Гомори.
Сначала решим задачу симплекс-методом. С этой целью приведем ее к каноническому виду, введя неотрицательные неизвестные 
, 
, 
. Получим систему ограничений:
(8.2)
, (8.3)
при которых ищем
Шаг 1: , , – базисные неизвестные; 
, 
– свободные неизвестные. Система ограничений (8.2) примет вид
(8.4)
Тогда (0; 0; 72; 16; 8) – базисное решение и 
.
Шаг 2: , , – базисные неизвестные; , – свободные неизвестные. Система ограничений (8.4) примет вид
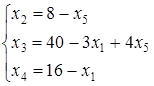(8.5)
Тогда (0; 8; 40; 16; 0) – базисное решение и 
примет значение 
.
Шаг 3: , , – базисные неизвестные; , – свободные неизвестные. Система ограничений (8.5) примет вид
(8.6)
Тогда 
– базисное решение и 
примет значение 
.
Так как в выражении F нет базисных переменных с положительными коэффициентами, то найденное базисное решение – оптимальное. Однако оно не удовлетворяет условию целочисленности. По методу Гомори сформируем по первому уравнению правильное отсечение, предварительно переписав его в виде:
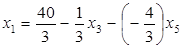
Имеем
;
;
Тогда дополнительное ограничение (8.1) запишем в виде
(8.1¢)
или после введения в него дополнительной целочисленной переменной 
.
Шаг 4: , , , 
– базисные неизвестные; , – свободные неизвестные. Система ограничений (8.6) дополнится еще одним уравнением:
(8.7)
Базисное решение 
недопустимое, т.к. 
. Согласно применяемому методу оно всегда получается недопустимым. Найдем допустимое базисное решение. Для этого переведем свободную переменную (или ) в базисную.
Шаг 5: , , , – базисные неизвестные; , – свободные неизвестные. Система ограничений (8.7) примет вид:
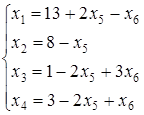
Тогда (13; 8; 1; 3; 0; 0) – базисное решение и 
примет значение 
.
Так как F не содержит положительных коэффициентов при свободных неизвестных, то найденное базисное решение оптимальное.
Ответ: , , 
.
Сформулируем ответ исходной экономической задачи.
Предприятие получит максимальную прибыль (74 млн. руб.), если установит в цехе 13 единиц оборудования первого типа и 8 единиц оборудования второго типа. При этом незанятая площадь в цехе составит 1 м2, в резерве для установки 3 единиц оборудования первого типа и ни одной единицы оборудования второго типа (шестая компонента содержательного смысла не имеет).
|
|
|
Замечание. Для геометрической интерпретации на плоскости отсечения (8.1¢) необходимо входящие в него переменные и выразить через переменные и . Имеем
или
Прямая l: 
, изображенная на рис. 8.1, проходит через точку K (13; 8), найденную методом I.
|
|
|
