 |
Закон сохранения момента импульса.
|
|
|
|
Для того чтобы сформулировать этот закон сохранения необходимо рассмотреть ряд определений.
Моментом импульса материальной точки относительно некоторой точки «0» (рисунок 3.6) называется вектор, равный векторному произведению радиус-вектора 
, проведенного из «0» в точку, где находится частица, на ее импульс 
:
(3.62)
 |  |
Обратите внимание на то, что, в соответствии с определением, вектор момента импульса всегда перпендикулярен плоскости образованной векторами и (рисунок 3.6). Поэтому если частица движется параллельно одной из осей координат, то мо-
мент импульса обязательно перпендикулярен ей (рисунок 3.7).
Модуль момента импульса
(3.63)
где 
- расстояние от направления движения частицы до точки «О» называется плечом момента импульса.
При равномерном вращении частицы вокруг точки «О» (рисунок 3.8) по окружности радиуса 
плечо момента импульса остается постоянным и равным , поэтому модуль вектора момент импульса
. (3.64)
Направление момента импульса перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.
Для определения направления момента импульса полезным может быть следующий прием: необходимо представить такое вращение некоторого твердого тела, при котором точка будет совершать заданное движение. Момент импульса направлен вдоль оси вращения в направлении, связанном с направлением вращения правилом правого винта.
Аналогично импульсу системы момент импульса системы частиц есть векторная сумма моментов импульса частиц входящих в систему:
(3.65)
Вращение относительно точки в технике встречается не часто. Гораздо чаще рассматривается вращение относительно оси. По определению в этом случае моментами импульса частицы и системы частиц относительно оси 
называются проекции соответствующих величин относительно точки, принадлежащей оси, на ось 
:
|
|
|
. (3.66)
Всякое вращение возникает под действием некоторых внешних сил. При этом воздействие внешних сил зависит не только от их величины, но и от ориентации в пространстве. Например, при вращении вокруг оси сила, направленная параллельно оси вращения не вызывает поворота тела. Эта особенность воздействия сил на тело при вращении учитывается введением в рассмотрение момента сил. По форме определение момента силы вполне аналогично определению момента импульса: моментом силы относительно точки называется векторная величина
|
(3.62)
где - есть радиус-вектор, проведенный из рассматриваемой точки (относительно которой рассматривается момент) в точку приложения силы.
Моментом силы 
относительно оси 
называется проекция момента силы относительно точки, принадлежащей оси на эту ось. Силу на рисунке 3.9 можно разложить на три взаимно перпендикулярных составляющих: 
- направленную параллельно оси вращения , 
- перпендикулярную оси вращения, 
- перпендикулярную плоскости, в которой лежит ось вращения, радиус-вектор и его составляющая, перпендикулярная оси вращения 
(плоскость 
). Составляющая создает момент, перпендикулярный плоскости . Его проекция на ось равна нулю. Аналогично момент составляющей не может вызвать вращения вокруг оси , поскольку ее момент перпендикулярен плоскости . Поэтому фактически момент силы относительно оси оказывается равным
. (3.63)
Рассмотрим теперь систему, состоящую из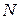 
взаимодействующих частиц. Уравнение движения 
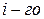тела системы имеет вид:
(3.64)
Аналогичным образом выглядят уравнения движения каждого из тел системы. Умножим левую и правую часть уравнения (3.64) векторно на соответствующий радиус вектор:
|
|
|
(3.65)
Сложим левые и правые части всех уравнений движения вида 3.65):
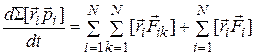. (3.66)
В левой части (3.66), в соответствии с определением стоит сумма моментов импульсов тел системы, равная моменту импульса системы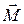 
в целом. Двойная сумма в правой части состоит из одинаковых пар слагаемых с противоположными по 3 закону Ньютона знаками. Поэтому она равна нулю. Вторая сумма в правой части представляет собой сумму моментов внешних сил 
, действующих на тела системы, и соотношение (3.58) приводится к виду:
. (3.67)
Соотношение (3.67) означает, что скорость изменения момента импульса системы равна суммарному моменту сил, действующих на тела системы. (Сравните это утверждение со вторым законом Ньютона!)
При рассмотрении вращения относительно оси следует взять проекцию (3.67) на ось вращения:
. (3.68)
Если рассматриваемая система является замкнутой, то
или 
. (3.69)
Это означает, что момент импульса замкнутой системы тел остается постоянным. Это утверждение называют законом сохранения момента импульса.
|
|
|
