 |
Потенциальная энергия упруго деформированного тела
|
|
|
|
При упругой деформации стержня сила 
, приложенная к стержню, совершает работу:
(3.50)
Преобразуем это выражение так, чтобы в него вошли параметры деформируемого тела вместо жесткости 
. Для этого подставим в выражение закона Гука 
относительную деформацию 
и механическое напряжение 
:
. (3.51)
Из (3.51) следует, что
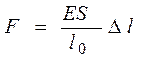, (3.52)
поэтому можно считать, что 
. Подставив это значение в формулу для работы (3.50), получим (очевидно, что в нашем случае удлинение стержня 
и координата его конца равны):
(3.53)
Работа внешней силы идет на увеличение запаса потенциальной энергии деформированного тела: 
. Если стержень однородный, то его деформация равномерно распределена по объему стержня. Тогда энергию деформации также можно считать равномерно распределенной по объему стержня, с плотностью энергии упругой деформации:
. (3.54)
ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Рассмотрим теперь общий случай: пусть имеется система из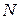 
частиц, взаимодействующих между собой посредством консервативных сил, и одновременно находящихся под действием внешних консервативных и неконсервативных сил.
Получим выражение для работы, совершаемой над частицами системы, при перемещении системы из одного положения в другое и одновременном изменении конфигурации системы. Обозначим работу внешних консервативных сил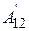 
. Эта работа равна убыли потенциальной энергии во внешнем поле сил:
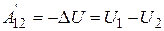. (3.55)
Для работы внутренних консервативных сил при изменении конфигурации системы справедливо аналогичное выражение:
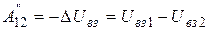. (3.56)
Обозначим работу неконсервативных сил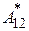 
. Вспомним, сформулированное нами ранее утверждение: суммарная работа идет на приращение кинетической энергии системы. Тогда можно записать соотношение:
|
|
|
. (3.57)
Подставим в левую часть выражения для работы консервативных сил:
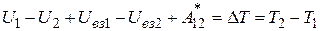, (3.53)
Или, после перегруппировки слагаемых по индексам,
. (3.54)
Обозначим сумму 
. Эта сумма, по определению, представляет собой полную механическую энергию системы. Тогда из (3.54) следует, что приращение полной энергии системы
(3.55)
равно работе не консервативных сил.
В частном случае, при их отсутствии, полная энергия не изменяется:
. (3.56)
Таким образом, полная механическая энергия системы материальных точек, находящихся под действием только консервативных сил, остается постоянной. Это утверждение называют законом сохранения механической энергии.
УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Рассмотрим частицу, на которую действуют только консервативные силы. Если в некотором состоянии результирующая сил, действующих на частицу равна нулю, то говорят, что частица находится в состоянии равновесия. В зависимости от последствий незначительного отклонения системы от положения равновесия различают:
§ устойчивое равновесие – если возникают силы, возвращающие систему в положение равновесия (рисунок 2.3 – 1);
- неустойчивое равновесие – если возникают силы, удаляющие систему от равновесия (рисунок 2.3 – 2);
- безразличное равновесие – если в новом положении система также оказывается в положении равновесия (рисунок 2.3 – 3).
 |
Равенство нулю сил, действующих на тело, указывает, в соответствии с соотношением (3.38)
, что первая производная потенциальной энергии при перемещении в направлении вывода из положения равновесия равна нулю.
Знак второй производной определяет вид экстремума функции вдоль направления движения тела. Поэтому условия равновесия тела (в случае одномерного движения) можно сформулировать следующим образом:
 |
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА.
ЦЕНТР МАСС И ЕГО ДВИЖЕНИЕ
|
|
|
Вторым аддитивным интегралом движения, сохраняющимся для замкнутой системы является её импульс.
Рассмотрим систему взаимодействующих частиц. На i -тую частицу системы действуют внутренние силы 
и внешне с результирующей 
. Уравнение движения i -той частицы имеет вид:
(3.57)
Аналогичные уравнения, очевидно можно записать для каждой из 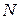частиц. Сложив левые и правые части уравнений, получим
(3.58)
Двойная сумма в (3.58) представляет собой сумму всех внутренних сил системы. По третьему закону Ньютона 
, и для каждого слагаемого в этой сумме найдется противоположный ему вектор. Поэтому 
.
По определению импульсом системы называют векторную сумму импульсов тел системы, т.е. величину 
. Таким образом, в левой части (3.58) стоит производная импульса системы. Если система замкнута, то из (3.58) следует, что
(3.58)
Таким образом, импульс замкнутой системы материальных точек остается постоянным. Это утверждение называют законом сохранения импульса.
Требование отсутствия внешних сил не является жестким. Если в пространстве существует такое направление, что проекция суммы результирующих внешних сил на него равна нулю, то, в соответствии с (3.58), проекция импульса системы на это направление будет оставаться постоянной.
Важным свойством обладает точка, называемая центром масс системы. Если система образована материальными точками с массами 
, а их положение задается радиус-векторами 
, то по определению центром масс называется точка, положение которой задается радиус-вектором 
, определяемым следующим выражением:
(3.59)
где 
есть масса всей системы.
Взяв производную от выражения (48), получим скорость центра инерции:
(3.60)
Как видно из (3.60) импульс системы
(3.61)
равен произведению ее массы на скорость центра инерции.
Кроме того, соотношение (3.58) позволяет утверждать, что если система замкнута, то ее центр масс движется равномерно и прямолинейно или покоится.
|
|
|
