 |
Принцип относительности Галилея
|
|
|
|
Рассмотрим две инерциальные системы отсчета и обозначим одну из них 
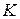, а другую 
. Будем считать, что оси координат сориентированы так, как это показано на рисунке 1.2. (Отметим, что столь специальный выбор взаимной ориентации осей координат обеспечивает существенное упрощение сопутствующих математических выкладок, а результаты, которые мы будем обсуждать, имеют общий характер, т.е. справедливы при произвольной ориентации осей координат.) Будем считать систему 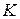неподвижной, а систему движущейся относительно 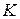со скоростью 
, направленной вдоль оси x (
).
Представим себе неподвижную в точку 
. Координаты этой точки системе отсчета –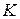 
и время 
связаны с координатами и временем в очевидными соотношениями:
. (1.8)
Система уравнений (1.8), уравнения которой связывают координаты точки в неподвижной и движущейся системах отсчета, называется преобразованиями Галилея.
Чтобы найти связь между компонентами векторов скоростей в 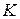и продифференцируем уравнения (1.8) по времени:
. (1.9)
Соотношения (1.9) можно заменить одним векторным:
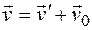, (1.10)
Которое выражает правило сложения скоростей в классической механике.
Дифференцируя (1.10) по времени, найдем связь между ускорениями в 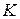и :
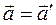. (1.10)
Соотношение (1.10) указывает на то, что ускорение тела во всех системах отсчета, движущихся равномерно и прямолинейно одинаково. Поэтому если одна из таких систем отсчета инерциальна, то и все другие также являются инерциальными.
Другой важный вывод, который следует из соотношения (1.10) заключается в следующем. Поскольку в основное уравнение динамики (1.6) из кинематических величин входит только ускорение, масса тел одинакова в различных системах отсчета, то и силы, действующие на тело в системах 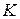и , должны быть одинаковы. Это означает, что уравнения динамики не изменяются при переходе от одной инерциальной системы отсчета к другой и все инерциальные системы отсчета эквивалентны.
|
|
|
Иными словами это утверждение принято формулировать следующим образом: уравнения динамики инвариантны (т.е. неизменны) по отношению к преобразованию координат, соответствующему переходу от одной инерциальной системы отсчета к другой (т.е. по отношению к преобразованиям Галилея). Это положение было установлено еще Галилеем и позволяет утверждать, что посредством проведения механических экспериментов невозможно определить, движется ли данная система отсчета равномерно и прямолинейно, или покоится. Если система отсчета неинециальна, движется неравномерно, с ускорением, то это легко обнаруживается экспериментально (Придумайте такой эксперимент!). А вот, например, равномерное и прямолинейное движение теплохода обнаружить механическими экспериментами невозможно.
Утверждение о том, что никакими механическими опытами невозможно установить движется ли данная инерциальная система отсчета равномерно и прямолинейно или покоится, называется ПРИНЦИПОМ ОТНОСИТЕЛЬНОС-ТИ ГАЛИЛЕЯ.
ВИДЫ СИЛ В МЕХАНИКЕ
Изучить самостоятельно:
2.4.1. Фундаментальные взаимодействия
2.4.2. Закон всемирного тяготения, гравитационная постоянная.
2.4.3. Природа сил упругости и сил трения.
2.4.4. Упругие силы, относительная деформация, механическое напряжение, закон Гука.
2.4.5. Внутреннее и внешнее трение. Вязкое трение, трение скольжения и качения.
2.4.6. Сила трения покоя. Коэффициент трения.
2.4.7. Зависимость силы трения скольжения от относительной скорости движения трущихся тел.
2.4.8. Сила тяготения, сила тяжести и вес тела. Вес тела в неинерциальных системах отсчета.
2.4.1. Упругие силы, относительная деформация, механическое напряжение, закон Гука.
|
|
|
При деформации тела возникают силы упругости. Деформацию называют упругой, если после прекращения действия внешних сил тело восстанавливает свою форму.
Остановимся на деформациях вида растяжение–сжатие. Допустим, что под действием силы 
закрепленный слева стержень (рисунок 2.2) с первоначальной длиной 
и площадью сечения 
получает удлинение (абсолютную деформацию) 
, равное изменению координаты его конца. При этом его относительная деформация будет равна:
, (2.11)
И он будет находиться под механическим напряжением
, (2.12)
Если деформации упругие (!), то выполняется закон ГУКА, согласно которому деформация стержня пропорциональна приложенной силе (для пружин коэффициент пропорциональности часто называют жесткостью):
. (2.13)
Другая формулировка закона Гука утверждает, что
, (2.14)
где коэффициент пропорциональности 
называется МОДУЛЕМ ЮНГА.
Лекция № 3
ЗАКОНЫ СОХРАНЕНИЯ
СОХРАНЯЮЩИЕСЯ ВЕЛИЧИНЫ
Силы, действующие на тела рассматриваемой механической системы можно естественным образом разделить на внутренние и внешние. Внутренними будем называть силы, действующие между телами, принадлежащими рассматриваемой системе, внешними – возникающие при взаимодействии тел системы с телами, не принадлежащими системе.
Система называется замкнутой, если внешние силы отсутствуют.
Для замкнутых систем существуют такие.
Из множества интегралов движения интерес представляют только аддитивные. Таких интегралов существует только три, и ими являются энергия, импульс и момент импульса. Соответственно существуют три закона сохранения, которые связаны со свойствами пространства и времени.
Сохранение энергии связано с однородностью времени, т.е. равнозначностью всех моментов времени.
Сохранение импульса связано с однородностью пространства.
Сохранение момента импульса – с изотропностью пространства, т.е. одинаковостью его свойств по всем направлениям.
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Попытаемся ответить на вопрос: почему кинетическая энергия частицы выражается формулой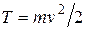 
?
С этой целью рассмотрим простейшую систему, состоящую из одной частицы. Уравнение движения частицы имеет вид
(3.1)
Под 
в (3.1) подразумевается результирующая сил, действующих на частницу.
|
|
|
Умножим (1) на 
:
(3.2)
Теперь учтем, что
, а 
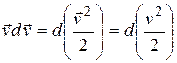(3.3)
Следовательно:
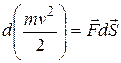(3.4)
Допустим, что на частицу не действуют внешние силы –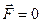 
, т.е. она представляет собой замкнутую систему 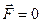. Тогда 
, и величина
. (3.5)
Это означает, что для изолированной частицы Т является интегралом движения, и который и называют кинетической энергией частицы.
РАБОТА И МОЩНОСТЬ
Механической работой силы 
на перемещении 
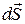называют скалярную величину
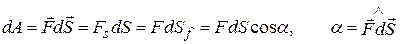. (3.6)
Подчеркнем, что эта величина является алгебраической и, если угол 
между и 
тупой, то сила совершает отрицательную работу. Напомним, что в СИ работа измеряется в джоулях (1 Дж = 1 Н * 1м).
Необходимо отметить отличие бытового понимания слова «работа» и понятия «механическая работа». Обратите внимание на то, что человек, переместивший горизонтально предмет в руке, механической работы не совершил, хотя с его точки зрения «свою работу выполнил».
Для вычисления работы на произвольном пути S необходимо сложить работы на элементарных перемещениях, т.е. найти интеграл
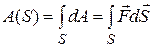(3.7)
Возвращаясь к рассматривавшейся нами частице, отметим, что если результирующая сил, действующих на частицу не равна нулю, то кинетическая энергия за все время 
получает приращение:
(3.8)
Если частица перемещается из точки 1 в точку 2 вдоль некоторой траектории, то, интегрируя соотношение (3.8) вдоль этой траектории, мы получаем:
(3.9)
Левая часть (3.9) представляет собой разность кинетических энергий в точках 1 и 2, а правая – работу результирующей силы:
(3.10)
Таким образом, приходим к выводу: работа результирующей силы идет на приращение кинетической энергии.
Отметим, что элементарное перемещение 
можно представить в виде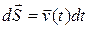 
и вычислять работу в промежутке времени от 
до 
по формуле:
(3.11)
Часто представляет интерес скорость совершения работы. Эту величину называют мощностью:
. (3.12)
Единицей измерения мощности является ватт: 1 Вт = 1 Дж/с.
|
|
|
