Энергия заряженного проводника
Заряд 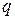 , сообщенный проводнику, можно рассматривать как систему точечных зарядов
, сообщенный проводнику, можно рассматривать как систему точечных зарядов 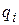 . Энергия такой системы зарядов определяется соотношением
. Энергия такой системы зарядов определяется соотношением

.
где 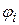 потенциал, создаваемый в точке, где находится i- тый заряд системы всеми остальными зарядами. Однако поверхность проводника является эквипотенциальной, т.е. потенциалы
потенциал, создаваемый в точке, где находится i- тый заряд системы всеми остальными зарядами. Однако поверхность проводника является эквипотенциальной, т.е. потенциалы 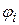 одинаковы, и соотношение (16.13) упрощается:
одинаковы, и соотношение (16.13) упрощается:

.
Поскольку заряд, потенциал и электроемкость проводника связаны соотношением  , выражение для энергии можно представить в виде:
, выражение для энергии можно представить в виде:

.
Энергия заряженного конденсатора
Заряд  положительно заряженной обкладки конденсатора находится в практически однородном поле отрицательно заряженной пластины в точках с потенциалом
положительно заряженной обкладки конденсатора находится в практически однородном поле отрицательно заряженной пластины в точках с потенциалом  . Аналогичным образом отрицательный заряд
. Аналогичным образом отрицательный заряд 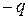 находится в точках с потенциалом
находится в точках с потенциалом 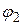 . Поэтому энергия конденсатора
. Поэтому энергия конденсатора
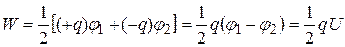
.
Очевидно, что эту формулу можно представить в виде
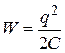
.
или
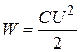
.
Формула (16.17) связывает энергию конденсатора с наличием на его обкладках заряда, а (16.18) – с существованием в промежутке между обкладками электрического поля. В связи с этим возникает вопрос о локализации энергии электрического поля: на зарядах или в пространстве между обкладками. В рамках электростатики ответить на этот вопрос невозможно, однако электродинамика утверждает, что электрическое и магнитное поля могут существовать независимо от зарядов. Поэтому энергия конденсатора сосредоточена в пространстве между обкладками конденсатора и связана с электрическим полем конденсатора.
Поскольку поле плоского конденсатора является однородным, можно считать, что энергия распределена между обкладками конденсатора с некоторой постоянной плотностью 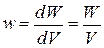 . В соответствии с соотношением (16.18)
. В соответствии с соотношением (16.18)
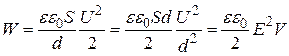
.
Поэтому плотность энергии электрического поля конденсатора оказывается равной
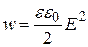
.
Учтем, что  , т.е. электрической индукции. Тогда выражению для плотности энергии можно придать вид:
, т.е. электрической индукции. Тогда выражению для плотности энергии можно придать вид:
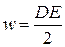
.
Электрическая индукция в соответствии с определением:
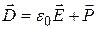
,
где 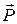 - поляризованность диэлектрика между обкладками конденсатора. Тогда выражение для плотности энергии приобретает вид:
- поляризованность диэлектрика между обкладками конденсатора. Тогда выражение для плотности энергии приобретает вид:
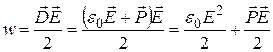
.
Первое слагаемое в правой части (16.23) представляет собой энергию, которой обладал бы конденсатор, если в пространстве между обкладками был бы вакуум. Второе слагаемое связано с энергией, затрачиваемой при зарядке конденсатора на поляризацию диэлектрика, заключенного в пространстве между обкладками.
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Электрический ток.
ЭТ будем называть упорядоченное (направленное) движение заряженных частиц, при котором через некоторую воображаемую поверхность переносится отличный от нуля электрический заряд. Обратите внимание, определяющим признаком существования электрического тока проводимоти является именно перенос заряда, а не направленное движение заряженных частиц. Любое тело состоит из заряженных частиц, которые вместе с телом могут двигаться направленно. Однако без переноса заряда электрический ток, очевидно, не возникает.
Частицы, осуществляющие перенос заряда, называются носителями тока. Количественно электрический ток характеризуют силой тока, равной заряду, переносимому через рассматриваемую поверхность в единицу времени:
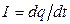
Вектором плотности тока называют вектор, модуль которого

,
направленный в сторону вектора скорости  положительных носителей тока. В формуле (1)
положительных носителей тока. В формуле (1) 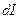 - сила тока через площадку
- сила тока через площадку 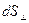 , расположенную перпендикулярно направлению движения носителей тока.
, расположенную перпендикулярно направлению движения носителей тока.
Пусть в единице объема содержится п+ положительных носителей с зарядом е+ и п– отрицательных с зарядом е–. Под действием электрического поля носители приобретают средние скорости направленного движения соответственно 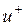 и
и  . За единицу времени через единичную площадку пройдут
. За единицу времени через единичную площадку пройдут 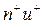 носителей, которые перенесут положительный заряд
носителей, которые перенесут положительный заряд  . Отрицательные перенесут соответственно заряд
. Отрицательные перенесут соответственно заряд 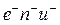 . Следовательно
. Следовательно
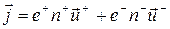
Уравнение непрерывности
Рассмотрим среду, в которой течет электрический ток. В каждой точке, среды вектор плотности тока 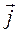 имеет определенное значение. Следовательно, можно говорить о поле вектора плотности тока и линиях этого вектора.
имеет определенное значение. Следовательно, можно говорить о поле вектора плотности тока и линиях этого вектора.
Рассмотрим поток 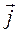 через некоторую произвольную замкнутую поверхность S. По определению
через некоторую произвольную замкнутую поверхность S. По определению 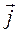 , его поток дает заряд, выходящий в единицу времени из объема V, ограниченного S. С учетом закона сохранения заряда можно утверждать, что поток
, его поток дает заряд, выходящий в единицу времени из объема V, ограниченного S. С учетом закона сохранения заряда можно утверждать, что поток 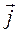 должен быть равен скорости убывания заряда в V:
должен быть равен скорости убывания заряда в V:
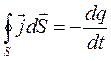
Но 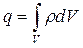 и поэтому
и поэтому
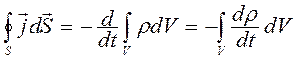
По теореме О. – Г.
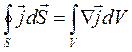
Следовательно
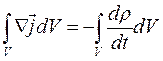
Равенство (17.7) должно выполняться при произвольном выборе объёма V, по которому производится интегрирование. Поэтому в каждой точке среды

Соотношение (17.8) называется уравнением непрерывности. Оно отражает закон сохранения электрического заряда и утверждает, что в точках, которые являются источниками вектора 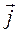 ,происходит убывание электрического заряда.
,происходит убывание электрического заряда.
В случае стационарного, т.е. установившегося (неизменяющегося) тока, потенциал, плотность заряда и др. величины являются неизменными и
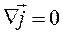
Это соотношение означает, что в случае постоянного тока вектор 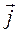 не имеет источников, а значит линии
не имеет источников, а значит линии 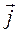 нигде ни начинаются и нигде не заканчиваются, т.е. линии постоянного тока всегда замкнуты.
нигде ни начинаются и нигде не заканчиваются, т.е. линии постоянного тока всегда замкнуты.
Электродвижущая сила
После снятия электрического поля, создававшего в проводнике электрический ток, направленное движение электрических зарядов быстро прекращается. Для поддержания тока необходимо от конца проводника с меньшим потенциалом переводить заряды к концу с большим потенциалом. Поскольку циркуляция вектора напряженности электрического поля равна нулю, то в замкнутой цепи кроме участков, на которых положительные носители движутся в сторону убывания потенциала, должны быть участки, на которых происходит перенос положительных зарядов в направлении возрастания потенциала. На этих участках перемещение зарядов может осуществляться только с помощью сил неэлектростатического происхождения, которые называют сторонними силами.
Сторонние силы можно охарактеризовать работой, совершаемой над перемещающимися по цепи зарядами. Электродвижущей силой называют величину, равную работе сторонних сил над единичным положительным зарядом:
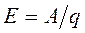
По аналогии с электростатическим полем стороннюю силу  можно представить в виде:
можно представить в виде:
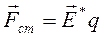
где 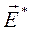 - напряженность поля сторонних сил.
- напряженность поля сторонних сил.
Работа сторонних сил на некотором участке цепи 1-2
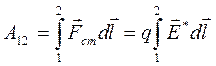
А значит, ЭДС на этом участке

Соответственно ЭДС, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил по этой цепи.
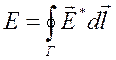
В общем случае на заряды кроме сторонних сил действуют электрические силы 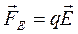 , так что результирующая сила
, так что результирующая сила
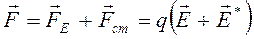
Работа, совершаемая результирующей силой на некотором участке цепи 1-2
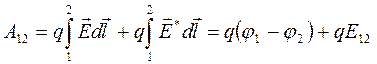
Падением напряжения на участке цепи 1 – 2 называется величина U 12, численно равная работе сторонних и электростатических сил при перемещении положительного единичного заряда. На оснований формулы (14)
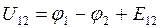
Если на участке цепи действуют сторонние силы, то он называется неоднородным в противном случае – однородным. Очевидно, что для однородного участка цепи 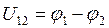 :
:
Воспользуйтесь поиском по сайту:


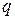 , сообщенный проводнику, можно рассматривать как систему точечных зарядов
, сообщенный проводнику, можно рассматривать как систему точечных зарядов 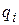 . Энергия такой системы зарядов определяется соотношением
. Энергия такой системы зарядов определяется соотношением .
.
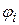 потенциал, создаваемый в точке, где находится i- тый заряд системы всеми остальными зарядами. Однако поверхность проводника является эквипотенциальной, т.е. потенциалы
потенциал, создаваемый в точке, где находится i- тый заряд системы всеми остальными зарядами. Однако поверхность проводника является эквипотенциальной, т.е. потенциалы 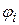 одинаковы, и соотношение (16.13) упрощается:
одинаковы, и соотношение (16.13) упрощается: .
.
 , выражение для энергии можно представить в виде:
, выражение для энергии можно представить в виде: .
.
 положительно заряженной обкладки конденсатора находится в практически однородном поле отрицательно заряженной пластины в точках с потенциалом
положительно заряженной обкладки конденсатора находится в практически однородном поле отрицательно заряженной пластины в точках с потенциалом  . Аналогичным образом отрицательный заряд
. Аналогичным образом отрицательный заряд 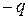 находится в точках с потенциалом
находится в точках с потенциалом 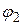 . Поэтому энергия конденсатора
. Поэтому энергия конденсатора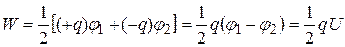 .
.
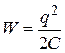 .
.
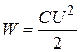 .
.
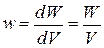 . В соответствии с соотношением (16.18)
. В соответствии с соотношением (16.18)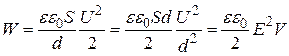 .
.
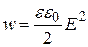 .
.
 , т.е. электрической индукции. Тогда выражению для плотности энергии можно придать вид:
, т.е. электрической индукции. Тогда выражению для плотности энергии можно придать вид: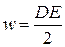 .
.
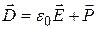 ,
,
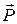 - поляризованность диэлектрика между обкладками конденсатора. Тогда выражение для плотности энергии приобретает вид:
- поляризованность диэлектрика между обкладками конденсатора. Тогда выражение для плотности энергии приобретает вид: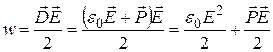 .
.
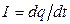
 ,
,
 положительных носителей тока. В формуле (1)
положительных носителей тока. В формуле (1) 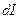 - сила тока через площадку
- сила тока через площадку 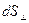 , расположенную перпендикулярно направлению движения носителей тока.
, расположенную перпендикулярно направлению движения носителей тока.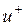 и
и  . За единицу времени через единичную площадку пройдут
. За единицу времени через единичную площадку пройдут 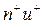 носителей, которые перенесут положительный заряд
носителей, которые перенесут положительный заряд  . Отрицательные перенесут соответственно заряд
. Отрицательные перенесут соответственно заряд 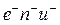 . Следовательно
. Следовательно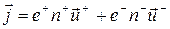
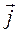 имеет определенное значение. Следовательно, можно говорить о поле вектора плотности тока и линиях этого вектора.
имеет определенное значение. Следовательно, можно говорить о поле вектора плотности тока и линиях этого вектора.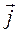 через некоторую произвольную замкнутую поверхность S. По определению
через некоторую произвольную замкнутую поверхность S. По определению 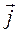 , его поток дает заряд, выходящий в единицу времени из объема V, ограниченного S. С учетом закона сохранения заряда можно утверждать, что поток
, его поток дает заряд, выходящий в единицу времени из объема V, ограниченного S. С учетом закона сохранения заряда можно утверждать, что поток 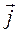 должен быть равен скорости убывания заряда в V:
должен быть равен скорости убывания заряда в V: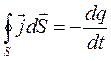
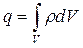 и поэтому
и поэтому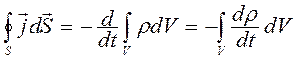
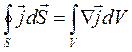
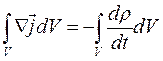

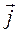 ,происходит убывание электрического заряда.
,происходит убывание электрического заряда.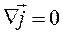
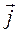 не имеет источников, а значит линии
не имеет источников, а значит линии 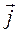 нигде ни начинаются и нигде не заканчиваются, т.е. линии постоянного тока всегда замкнуты.
нигде ни начинаются и нигде не заканчиваются, т.е. линии постоянного тока всегда замкнуты.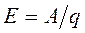
 можно представить в виде:
можно представить в виде: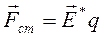
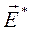 - напряженность поля сторонних сил.
- напряженность поля сторонних сил.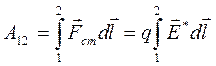

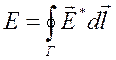
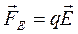 , так что результирующая сила
, так что результирующая сила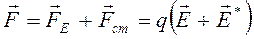
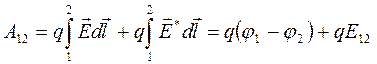
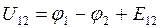
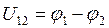 :
:

