Основные представления элементарная классической теории электропроводности металлов

Исходя из того, что в металлах имеется порядка 10²⁸ - 10²⁹ м ^-3 практи­чески свободных электронов Друде создал классическую теорию электропровод­ности металлов, которую в последствии усовершенствовал Лоренц.

Согласно представлениям этой теории электроны в металле ведут себя аналогично молекулам идеального газа, и при своем движении имеют среднюю длину свободного пробега 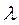. Предполагается, что электроны сталкиваются в основном с ионами кристаллической решетки, что приводит к установлению теплового равновесия между электронным газом и кристаллической решеткой.

Оценим на основе кинетических представлений скорость теплового движе­ния электронов:

(1)

Для сравнения найдем среднюю скорость упорядоченного движения электронов при прохождении тока. Технически максимальная плотность тока в

медных проводах составляет 10⁷ А/м². Учитывая, что находим:

(2)

Таким образом, даже при максимальных плотностях тока скорость направленного движения электронов примерно на 8 порядков меньше скорости теплового движе­ния. Следовательно, модуль результирующей скорости можно считать равным теп­ловой скорости.

Найдем в изменение кинетической энергии электронов, обусловленное их участием в направленном движении под действием поля. Средний квадрат результирующей скорости равен

(3)

Движение электрона с тепловой скоростью и скоростью направленного

движения являются статистически независимыми событиями. Поэтому

и поскольку , 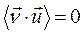(4)

Следовательно

(5)

А значив направленное движение увеличивает кинетическую энергию электронов в в среднем на

(6)

В теории Друде предполагается, что при столкновениях электронов с ионами кристаллической решетки электроны полностью передают приобретенную в поле энергию, и непосредственно после столкновения скорость их направленного движения равна нулю.

 

Объяснение закона ОМА.

 

Будем считать поле, ускоряющее электроны, однородным. Тогда за время свободного пробега

(7)

двигаясь равноускоренно, электрон разгоняется до скорости

(8)

Следуя Друде, пренебрежем распределением электронов по скоростям и, будем считать, что у всех электронов тепловая скорость равна . Тогда

(9)

Среднее на длине свободного пробега значение скорости направленного движения.

, (10)

Сравнивая (10) с выражением для закона Ома в дифференциальной форме, находим (11)

Отметим, что если бы электроны не сталкивались бы с ионами, то была бы бесконечной, а удельное сопротивление - нулевым. Таким образом, в тео­рии Друде физическая природа сопротивления металлов состоит в столкновениях электронов с ионами решетки.

Объяснение закона Джоуля-Ленца

Закон Видемана – Франца и его объяснение

Затруднения классической электронной теории электропроводности металлов.

Согласно (11) сопротивление металлов должно возрастать пропорционально . Действительно, и следует считать независящими от , а скорость теплового движения пропорциональна . Экспериментально наблюдается пропорциональность не , а температуре в первой степени.

Второе затруднение заключается в том, что идеальный газ свободных элек­тронов должен обладать молярной теплоемкостью 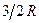. Эта теплоемкость должна складываться с решеточной теплоемкостью, равной . Следовательно, теплоемкость металлов должна быть примерно в 1,5 раза большей, чем у диэ­лектриков. В эксперименте такого не наблюдается.

Эффект Холла

Допустим, что у нас имеется прямоугольная металлическая пластинка, по которой течет постоянный ток с плотностью , направленный вдоль одного из ребер параллелепипеда. Поместив пластинку в однородное магнитное поле, направленное вдоль другого ребра. В 1879 году Холл обнаружил, что между гранями пластинки, параллельны векторам и возникает разность потенциалов

(12)

Коэффициент пропорциональное в (12) называют постоянной Холла; b - толщина пластинки. Это явление получило название эффект Холла или галъвано-магнитного явления.

Наиболее просто ЭХ объясняется классической электронной теорией. На электроны, движущиеся в пластинке воздействует магнитная составляющая силы Лоренца, в результате чего у них появляется составляющая скорости направленная к верхней грани пластинки. У этой грани образуется избыток от­рицательных носителей тока, а у противоположной - избыток положительных. Возникает электрическое поле с напряженностью , действие которого ком­пенсирует действие силы Лоренца. В стационарном состоянии

или (13)

Умножим (13) на b и выразим и через плотность тока: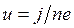

(14)

Тогда в левой части получаем разность потенциалов и, сравнивая с (12), най­дем: значение постоянной Холла:

(15)

Таким образом, измерив постоянную Холла, можно рассчитать концентрации но­сителей тока в проводнике.

Одним из важных параметров проводящих материалов является подвижность носителей тока. По определению подвижностью называется величина, равная средней скорости направленного движения носителей тока в электричес­ком поле единичной напряженности:

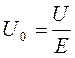(16)

Если соотношение разделить на Е, то, учитывая закон Ома и (16), получим важное соотношение:

(17)

Очевидно, что, измерив постоянную Холла и проводимость материала, можно рас­считать подвижность (холловскую) и концентрацию носителей тока.

МИНОБРНАУКИ РОССИИ

Институт сферы обслуживания и предпринимательства (филиал)
федерального государственного бюджетного образовательного учреждения
высшего профессионального образования
«Донской государственный технический университет»
в г. Шахты Ростовской области

(ИСО и П (филиал) ДГТУ)

 

УТВЕРЖДАЮ

Заведующий кафедрой ЕНД

 

___________(П.Н. Козаченко)

«04» сентября 2013 г.

 

На правах рукописи

Физика

Конспект лекций

(Часть 4. Электромагнитные явления)

 

Для студентов направления 230400

«Информационные системы и технологии»

 

Электронный образовательный ресурс

 

 

Составитель: к.ф.-м.н., доцент В.В. Коноваленко

 

Рассмотрен и рекомендован для использования в учебном процессе на 2013/2014 – 2015/2016 уч. г. на заседании кафедры ЕНД.

Протокол № 1 от 04. 09. 2013 г.

 

Шахты 2013

 

МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

Взаимодействие токов

Самостоятельно: § 39.

⇐ Предыдущая22232425262728293031Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: