 |
Магнитное поле движущегося заряда.
|
|
|
|
Пространство изотропно, и если заряд неподвижен, то относительно точки, в которой он находится, все направления равноправны. Соответственно электростатическое поле точечного заряда является сферически симметричным.
Если заряд движется со скоростью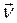 
, то в пространстве появляется выделенное направление - направление вектора 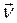, поэтому можно ожидать, что поле движущегося заряда обладает осевой симметрией. Индукция поля движущегося заряда в некоторой точке Р в момент времени t определяется положением заряда не в момент t, а в более ранний момент 
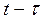, так как распространение поля в пространстве происходит с конечной скоростью с:
(18.3)
где 
- координаты точки Р в неподвижной системе отсчета;
- радиус-вектор проведенный в Р из точки, в которой находился заряд в момент времени .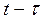
Если скорость движения заряда невелика - 
-, то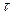 
пренебрежимо мало, и
(18.4)
Вид функции 
может быть установлен только опытным путем. В соответствии с экспериментом для 
(18.5)
где 
- магнитная постоянная, равная 4p 10 -7 Гн/м;
- единичный вектор, направленный вдоль 
.
Можно показать, что появление в пространстве выделенного направления при движении заряда приводит к тому, что электрическое ноле движущегося заряда становится осесимметричным, причём в направлениях, перпендикулярных 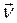поле становится больше, чем в направлении 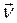- рисунок 1.
Закон Био-Савара-Лапласа.
Закон БСЛ позволяет вычислить индукцию поля в произвольной точке, которая создается проводников с током I.
Элемент проводника длиной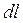 
и сечением 
содержит 
носителей тока (
- концентрация носителей). Каждый из носителей создает поле с индукцией
(18.6)
Среднее по всем носителям тока в элементе 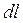значение индукции
|
|
|
(18.7)
Умножив (18.7) на количество носителей тока в 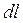, получим индукцию, создаваемую элементом :
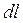(18.8)
Поскольку 
, выражение (18.8) принимает вид:
. (18.9)
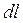можно рассматривать как вектор, направленный вдоль 
, и считать
(18.10)
Соответственно получаем:
(18.11)
Соотношение (18.11) называется законом Био-Савара-Лапласа.
Вычисление индукции поля прямого тока
Индукция поля прямого тока находится по формуле 
. Вывод этой формулы на основе закона Био-Савара-Лапласа изучить самостоятельно: § 42.
Сила Лоренца
На движущийся в магнитном поле заряд действует сила, которую естественно называть магнитной. Логично предположить, что эта сила должна быть пропорциональна величине заряда q, его скорости 
и индукции магнитного поля 
. Действительно, экспериментально установлено, что
(18.12)
Отметим, что, в соответствии с определением, магнитная сила всегда перпендикулярна скорости заряда и индукции поля, а значит - работы над зарядом не совершает. (18.А = 0)
Если на заряженную частицу одновременно действуют электрическое и магнитное поля, то результирующая сила будет равна
(18.13)
Эта сила называется силой Лоренца.
Закон Ампера
Закон Ампера определяет силу, действующую на проводник с током в магнитном поле. Получим формулу закона Ампера, исходя из выражения для силы Лоренца.
На каждый из носителей тока в проводнике, находящемся в магнитном поле действует сила
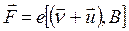(18.14)
За счет взаимодействия носителей тока с остальным веществом проводника эта сила передается всему проводнику в целом. Усредняя силу (18.14) по всем носителям тока находящимся в элементе 
проводника, получаем:
(18.15)
Число носителей тока в элементе 
равно, очевидно, 
. Умножив, (18.15) на это число, получим
(18.16)
Учтем, что 
, а 
. Тогда (18.16) приводится к виду:
(18.17)
Формула (18.17) определяет силу, действующую на элемент тока 
в магнитном поле, и выражает закон Ампера.
|
|
|
|
|
|
