 |
Свободных электронов в металле
|
|
|
|
Волновая функция должна удовлетворять граничным условиям, которые в общем случае называются циклическими граничнымиусловиями Борна – Кармана. Смысл этих условий заключается в следующем. Если представить, что некоторый объем заполняется одинаковыми образцами металла, идентичными рассматриваемому, то волновая функция должна повторяться в пределах каждого образца. Поэтому волновая функция должна быть периодической по всем координатам с периодом L., Функция (38.06) будет удовлетворять этому требованию, если независимо друг от друга будут выполняться условия:
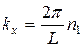
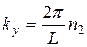и 
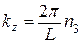(38.07)
где n 1, n 2, n 3 могут независимо принимать значения 0, ±1, ±2, …
Условия (38.07) соответствуют тому, что при переходе на расстояние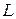 
вдоль любой из осей координат мы оказываемся в эквивалентной точке кристалла. Действительно такой переход означает замену 
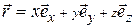на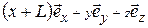 
, что эквивалентно умножению волновой функции на множитель 
, что не изменяет её.
Таким образом, периодические граничные условиятребуют дискретного изменения волнового вектора электрона в кристалле. Другими словами значения волнового вектора электронов квантуются.
Следствием квантования волнового вектора является квантование энергии электронов. Действительно, подставив (38.07) в (38.04), получим:
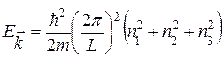(38.07)
Кроме волнового вектора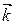 
состояние электрона в металле определяется еще спиновым квантовым числом 
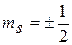. Поэтому можно утверждать, что состояние электрона в кристалле будет определено, если заданы четыре квантовых числа
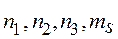. (38.08)
Энергия электронов определяется суммой квадратов чисел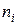 
. Очевидно, что одной и той же сумме квадратов соответствует несколько различных комбинаций чисел 
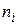. А значит, уровни энергии являются вырожденными, причем число комбинаций квантовых чисел, отвечающих данному уровню, быстро растет с ростом энергии.
|
|
|
Рассмотрим воображаемое пространство, по осям которого будет откладывать значение квантовых чисел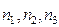 
. Каждой паре состояний (в соответствии с двумя значениями 
) в этом пространстве соответствует точка. Поверхность равных значений энергии имеет форму сферы радиуса
.
Число состояний 
, энергия которых не превышает некоторого значения 
, равно удвоенному количеству точек, содержащихся внутри сферы радиуса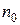 
. Точки расположены в пространстве волновых векторов (точнее в пространстве квантовых чисел 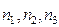.) с плотностью, по определению равной единице. Поэтому 
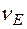определяется удвоенным объемом сферы:
(38.09)
Поскольку энергия электрона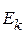 
с волновым вектором 
, определяемым набором квантовых чисел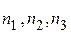 
,
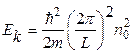(38.10)
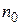можно представить в виде:
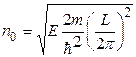(38.11)
Тогда для 
оказывается справедливым выражение
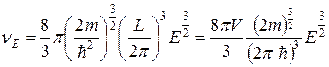(38.12)
где 
– объем рассматриваемого образца металла.
Функцией плотности состояний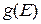 
называют функцию, описывающую зависимость количества энергетических уровней, приходящихся на единичный интервал энергий от энергии:
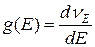(38.13)
Число состояний 
с энергией от Е до 
найдем дифференцируя (38.12) по энергии:
(38.14)
Из (38.14) следует, что функция плотности состояний электронов в металле пропорциональна корню из энергии:
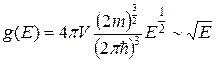(38.15)
График функции плотности состояний электронов в металле имеет вид, приблизительно показанный на рисунке 38.1.
Допустим, что концентрация свободных электронов в рассматриваемом металле равна 
. Тогда во всем образце содержится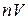 
свободных электронов. При абсолютном нуле все эти электроны располагаются в доступных состояниях с минимальной энергией по одному, в соответствии с принципом запрета Паули, в каждом состоянии, отличающемся хотя бы одним из квантовых чисел (38.08). Все состояния с энергией менее некоторого значения 
будут заполнены, остальные - свободны. Энергетический уровень , отделяющий занятые и свободные состояния называют уровнем Ферми при абсолютном нуле.
|
|
|
Итак, вследствие действия принципа запрета Паули энергия электронов даже при абсолютном нуле оказывается отнюдь не нулевой. Представляет интерес оценить величину в металлах и среднюю энергию при абсолютном нуле.
В пространстве волновых векторов (k -пространстве или пространстве импульсов, поскольку р = ћ k) поверхность постоянной энергии (изоэнергетическая поверхность) описывается уравнением:
(38.16)
Изоэнергетическая поверхность, соответствующая энергия 
, называется поверхностью Ферми. В модели свободных электронов, которую мы рассматриваем, поверхность Ферми
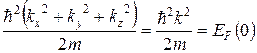(38.17)
является поверхностью сферы, которая при Т = 0 отделяет заполненные и свободные состояния. Общее количество состояний 
внутри поверхности Ферми с одной стороны равно количеству электронов в образце металла 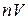, а с другой определяется формулой (38.12), если в ней положить энергию равной :
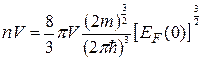(38.18)
(38.19)
Отметим, что уровень Ферми при абсолютном нуле в металлах оказался пропорционален 
.
Концентрация электронов в металлах имеет величину n ≈ 5∙ 1022 см -3. Тогда, подставив числовые значения в (38.19) получаем
≈ 5 эВ.
Сравним среднюю энергию электронов при Т = 0 и электронов идеального газа в модели классических свободных электронов. Суммарная энергия электронов заполняющих состояния с энергиями от Е до
(38.20)
Суммарная энергия всех электронов проводимости
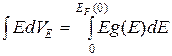(38.21)
Разделив эту энергию на полное число электронов (а оно равно числу состояний внутри сферы Ферми), получим среднюю энергию электрона:
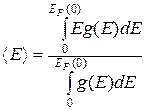(38.22)
Подставив сюда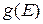 
из (38.15) (одинаковые коэффициенты в составе 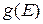в числителе и знаменателе сокращаются), получим
Это очень большая энергия. Чтобы частицам идеального газа сообщить в среднем такую энергию необходимо нагреть его до температур порядка 25000 К.
Этим, фактически, объясняется малый вклад электронного газа в теплоемкость металла.
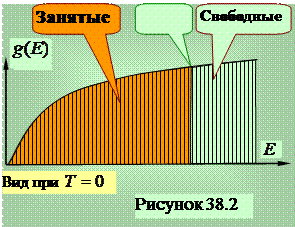Отметим (рисунок 38.2) на графике функции плотности состояний коричневым цветом область значений энергии электронов те уровни, которые при абсолютном нуле заняты электронами. Площадь под кривой дает количество занятых состояний, равное количеству электронов.
|
|
|
При нагревании металла до температур порядка комнатной электронный газ также увеличивает свою энергию, причем увеличение энергии электронов может составлять величину порядка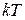 
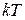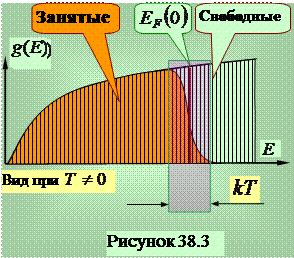
. Однако существенно то, что электроны заполненных уровней с низкой энергией получить дополнительную энергию не могут – энергетические уровни, отстоящие от них по оси энергии на расстоянии порядка заняты. Поэтому нагревание образцаровни лежащие вые энергии электронов может составлять величину порядка получить дополнительную энергию не могут сопровождается переходами электронов только с уровней, примыкающих к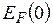 
. Кривая заполненных состояний принимает вид, показанный на рисунке 38.3. Площадь под кривой остается постоянной, поскольку количество электронов не изменяется. Область отличия от кривой на рисунке 38.2 имеет величину порядка .
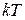Необходимо отметить, что отразить графически изменение кривой, описывающей заполненность состояний, в разумном масштабе не представляется возможным. При комнатной температуре область шириной 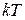на графике должна быть примерно в 100 раз уже отрезка, соответствующего 
. Т.е. на рисунке ширина области 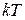очень сильно увеличена. При соблюдении масштаба рисунка по энергиям показанной области 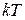соответствует положение примерно на расстоянии 100 см, т.е. далеко за пределами страницы.
Таким образом, при нагревании металла будет участвовать доля электронов порядка
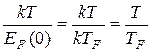(38.23)
где 
и называется температурой Ферми.
Соответственно молярная теплоемкость электронного газа составит
(38.24)
Положим при комнатной температуре Т = 300 К и температуре Ферми ТF = 25000 К, Сэл примерно в 100 раз меньше классического значения, т.е. не увеличивает теплоемкость металлов.
|
|
|
