Кристаллическая решетка, кристаллическая структура, индексы Миллера.

Отличительной особенностью кристаллов является упорядоченность в рас­положении атомов в пространстве, заключающаяся в том, что атомы располага­ются в узлах геометрически правильной пространственной решетки, называемой кристаллической решеткой. Следует отчетливо представлять, что кристалли­ческая решетка есть геометрическое понятие. Если с каждой точкой решетки мысленно связать некоторый атом или набор атомов, то получим модель кри­сталлической структуры, кристалла.

На рисунке 37.1 показан пример двумерной кристаллической решетки. Вся решетка может быть получена путем многократного повторения в пространстве одного и того же структурного элемента, называемого элементарной кристал­лической ячейкой (ЭКЯ). В двумерном случае элементарной ячейкой является параллелограмм, построенный на векторах и . В пространстве вместо паралле­лограмма надо представить в общем случае косоугольный параллелепи­пед, построенный на некомпланарных векторах , и . Выбор векторов для построения элементарной ячейки не является однозначным. Так векторы и также можно использовать для определения элементарной ячейки, однако обычно стараются выбрать элементарную ячейку кристалла так, чтобы ее симметрия со­ответствовала симметрии кристалла.

Векторы , и обычно принимаются в качестве ортов косоугольной, в общем случае, системы координат, которая используется для описания свойств кристалла. Положение точки с координатами внутри кристаллической ячейки принято характеризовать индексами точки, дробными числами, равными отношению координат к периодам идентичности:

.

Например, центр элементарной ячейки имеет индексы:

.

Направление в кристалле задают индексами направления. В качестве этих индексов принимают наименьшие целые числа , отношение которых равно отношению индексов любой точки, принадлежащей прямой, проходящей через начало координат и параллельной заданному направлению:

.

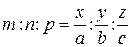Например, оси координат имеют индексы направлений:

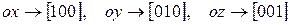
(для точек оси координаты y и z равны нулю). Противоположные направления описывают индексами:

(знак «-» ставится над соответствующим символом).

Положение плоскости в кристалле можно задать, указав величины отрезков , которые плоскость отсекает на осях координат. Однако принято в этом слу­чае использовать индексы Миллера: наименьшие целые числа h, k, l, отноше­ние которых

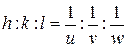
В общепринятых обозна­че­ниях плоскостей числа h, k, l за­ключают в круг­лые скобки, опус­кают запятые, а в случае наличия ми­нуса, отмечают его чертой над со­ответствующим числом. Напри­мер: (100), () и т.п. Основные плоскости в тетрагональном (элементарная ячейка – прямоугольный параллелепипед) кри­сталле показаны на рисунке 37.3. Отметим, что в кубическом кристалле на­правление и плоскость, в описании которых присутствуют одинаковые сим­волы, перпендикулярны: .

 

37.2 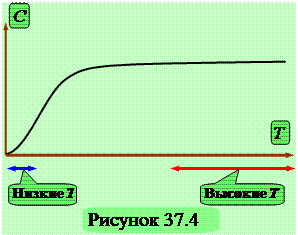Теплоемкость кристаллов. Классические представления и теория Эйнштейна

Закон Дюлонга и Пти утверждает, что все химически простые кристаллы имеют одинаковую молярную теплоемкость, равную . Этот закон основывается на классических представлениях о том, что кристалл, состоящий из атомов, имеет колебательных степеней свободы. На каждую из них приходится в среднем одинаковая энергия .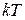

Экспериментальная проверка этого закона показала, что он хорошо выпол­няется при достаточно высоких температурах. При низких температурах (рисунок 37.4) теплоемкость уменьшалась, и стремилась к нулю приблизительно по закону .

Вспомним о том, что значение средней энергии на колебательную степень свободы, равное 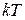получается в предположении о том, что постоянная Планка равна нулю, и энергия осцилляторов изменяется непрерывно. Атомы в кристалле подобны гармоническим квантовым осцилляторам, энергия которых изменяется дискретно В этом случае средняя энергия гармониче­ского осциллятора определяется соотношением:

. (37.01)

В отличие от соотношения, использовавшегося Планком, в (37.01) учтено нали­чие нулевых квантовых колебаний.

Эйнштейн предложил представить кристалл, состоящий из атомов, в виде системы, состоящей из независимыхквантовых осцилляторов с одина­ковой собственной частотой . Пренебрегая энергией нулевых квантовых колеба­ний (она становится заметной только при очень низких температурах, и о ее су­ществовании не было известно Эйнштейну), внутреннюю энергию кристалла можно представить в виде:

. (37.02)

 

Дифференцируя это соотношение по температуре, находим теплоемкость кри­сталла:

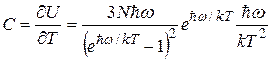. (37.03)

Представляет интерес рассмотреть два частных случая, соответствующих двум температурным областям: область высоких температур и область низких температур.

1. Будем считать высокими температуры, при которых выполняется соотно­шение

, (37.04)

т.е. классическое значение энергии на степень свободы осциллятора намного пре­восходит расстояние между уровнями гармонического квантового осциллятора. В этом случае приближенно можно считать и

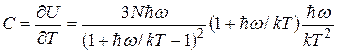. (37.05)

В числителе пренебрежем по сравнению с единицей:

. (37.06)

Положив , получаем закон Дюлонга и Пти.

2. В области низких температур выполняется обратное (37.04) соотноше­ние: .

В этом случае в знаменателе (37.03) можно пренебречь единицей, и для теплоем­кости получаем:

. (37.07)

При условии температурная зависимость определяется экспоненциаль­ным множителем, а значит теплоемкость, в рамках принятых пред­положений, стремится к нулю. Но изменение с температурой происходит по экс­поненциальному закону, в то время как экспериментально наблюдалась зависи­мость .

Таким образом теория Эйнштейна качественно верно описывает зави­симость теплоемкости от температуры в широком диапазоне температур, однако количественно не совпадает с экспериментом.

Количественного согласия теории и эксперимента удалось достичь Дебаю, который учел, что колебания атомов в кристалле не являются независимыми. Чтобы понять теорию Дебая, необходимо рассмотреть некоторые основные поло­жения теории колебаний.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: