Приближение сильно связанных электронов

39.1.1. Физическое обоснование приближения

Представим себе, что нам удалось расположить некоторое коли­чество атомов натрия в узлах объемоцентрированной кубической решетки (решетку такого типа имеет реальный кристалл натрия) со стороной около сантиметра. Все электроны атомов в этом случае бу­дут находиться на атомарных уровнях, локализованных в узлах ре­шетки и ничем не напоминающих комбинации плоских волн (волно­вые пакеты в приближении почти свободных электронов). Если те­перь плавно уменьшать постоянную решетки, искусственно выбран­ную большой, то в некоторый момент, еще задолго до того, как будет достиг­нуто реальное значение постоянной решетки, нам придется отказаться от отождествления электронных уровней решетки с атомными уров­нями отдельных атомов натрия.

 

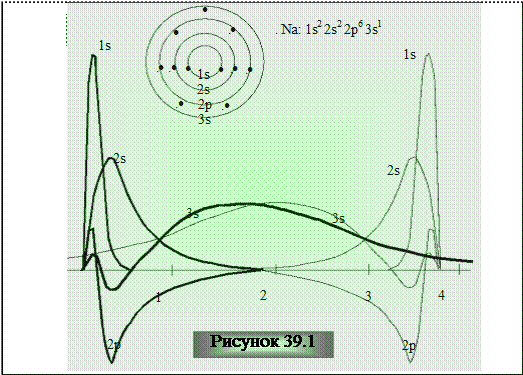Для конкретного атомного уровня это станет необходимым, когда межатомное расстояние станет срав­нимым с пространственной протяженностью его волновой функции: тогда электрон на этом уровне начнет ощущать присутствие соседних атомов. Реальное положение для атомарных уровней натрия показано на рисунке 39.1, где изображены волновые функции двух изолирован­ных атомов, расстояние между которыми составляет 3,7 ангстрема, что соответствует расстоянию в реальной кристаллической струк­туре. Перекрытие волновых функций 1s уровней практически отсут­ствует, и в кристалле такие уровни остаются неизменными. Перекры­тие волновых функций уровней 2s и 2р очень мало, и, надо полагать, в кристалле эти уровни мало отличаются от уровней изолированных атомов. Перекрытие волновых функций 3s уровней (содержащих ва­лентные электроны) весьма значительно, и эти уровни в кристалле должны сильно измениться.

39.1.2. Основные результаты решения уравнения Шредингера для электронов в кристалле в приближении сильно связанных электронов

В теории сильно связанного электрона в качестве нулевого при­ближения принимается гамильтониан электрона в изолированном атоме. Волновая функция электрона в кристалле представляет линейную комбинацию атомных волновых функций, удовлетворяю­щую требованию трансляционной симметрии.

Важнейшим результатом перекрытия волновых функций от­дельных атомов является тот факт, что электроны соседних атомов получают возможность переходить от одного атома к другому. Два любых атома могут обменяться своими электронами путем последо­вательных обменов электронами соседних атомов. При этом обмен происходит посредством поля всех ядер, однако, в силу экспоненциального паде­ния волновых функций по мере удаления от ядра, в основном в обмене участвуют соседние атомы. Другими словами электроны не локализуются у отдельных ядер, а, в известном смысле, свободно перемещаются по кристаллу, переходя от одного атома к другому.

Перемещение электрона по кристаллу в приближении сильно связанных электронов можно представлять происходящим вследствие квантовомеханического туннелирования. В соответствии с соотношением неопределенностей время пребывания электрона в некотором состоянии связано с шириной данного энергетического уровня соотношением неопределенностей. В изолированном атоме на стационарном уровне (в невозбужденном состоянии) электрон имеет вполне определенную энергию и пребывает на данном уровне неограниченно долго. В кристалле при расщепле­нии энергетических уровней в зону возникает неопределенность в энергии электрона, что обусловливает конечность вре­мени нахождения электрона вблизи данного узла кристаллической решетки. Расщепление внеш­них энергетических уровней составляет несколько электрон-вольт. Соответствующее время «оседлой жизни» электрона имеет величину порядка 10 ^-15 с. Расщепление внутренних уровней может составлять величину порядка 10 ^-19 эВ, а соответствующее время – около часа. Тем не менее, можно считать, что в стационарном состоянии электрон рас­пределен с одинаковой вероятностью по всем узлам решетки кри­сталла.

Результатом обменного взаимодействия атомов является, с одной стороны, понижение средней потенциальной энергии электронов в кристалле в поле всех ядер. Величина понижения энергии (обозначим ее С) определяется интегральным выражением, учиты­вающим влияние всех ионов кристаллической решетки. С другой стороны, результатом обменного взаимодействия является возникновение специфической обменной энергии, что и приводит к расщеплению уровня в полосу энергии с шириной, пропорциональной некоторому интегральному выражению (обозначим его А), опреде­ляемому волновыми функциями всех участвующих в обмене атомов и называемому обменным интегралом.

В случае простой кубической решетки С и А являются кон­стантами, и в первом приближении для энергии электрона справед­ливо выражение:

Е ₍₁₎ = Е (k) = Е _а + С + 2А (соs k_xa + cos k_y a + cos k_za). (39.1)

Энергия зависит квазинепрерывно от волнового вектора и изме­няется в пределах от Е _min до Е _max:

Е _min = Е _a + С - 6½А½, Е _max = Е _a + С + 6½А½ (39.2)

Таким образом, в результате взаимодействия атомов для простой кубической решетки уровень энергии изолированного атома опуска­ется на величину С и расщепляется в зону, шири­ной 12½ А ½.

Величина обменной энергии увеличивается при увеличении перекрытия волно­вых функций. Следовательно, уровни внутренних оболочек расщеп­ляются меньше, чем на­ружных, и с ростом энергии ширина разрешен­ных зон увели­чивается, а запрещенных уменьшается.

Внешние воздействия, приводящие к изменению расстояния ме­жду атомами (нагрев, механическая деформация) меняют область перекрытия волновых функций атомов, вследствие чего изменяется ширина разрешенных и запрещенных зон, эффективная масса элек­тронов, а значит и другие свойства полупроводника, зависящие от этих параметров.

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: