 |
Колебания систем с большим числом степеней свободы
|
|
|
|
Рассмотрим малые колебания системы, имеющей 
степеней свободы. Положение такой системы может быть задано с помощью некоторых величин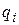 
, которые называются обобщенными координатами системы. Физическая природа этих величин может быть различна в различных системах, важно только то, что они определяют положение системы.
В теории колебаний доказывается, что такая система обладает собственными частотами 
(j = 1, 2, 3, … ). При произвольном (на самом деле не оптимальном выборе набора обобщенных координат системы) общее решение уравнения движения системы имеет вид суперпозиции гармонических колебаний с собственными частотами системы:
. (37.08)
При этом энергия системы описывается выражением:
. (37.09)
Первое слагаемое в (37.09) является аналогом потенциальной энергии гармонического осциллятора, но связывает отклонения из положения равновесия различных осцилляторов. Похожим образом второе слагаемое является аналогом кинетической энергии, но включает в себя произведения скоростей различных осцилляторов.
Можно показать, что при правильном выборе обобщенных координат системы (который всегда существует!) изменение каждой из них будет представлять собой простое (не суперпозицию!) гармоническое колебание, совершаемое на одной из собственных частот :
. (37.10)
Выбранные таким специальным образом обобщенные координаты называют нормальными, а совершаемыые колебания - нормальными колдебаниями.
Важнейшей особенностью нормальных колебаний является то, что энергия, системы оказывается равна сумме энергий каждого из нормальных колебаний:
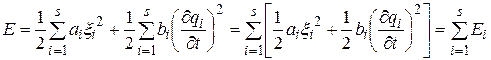. (37.11)
Чтобы понять отличие нормальных координат от произвольно выбранных просто обощенных координат рассмотрим систему, состоящую из двух одинаковых математических маятников длиной 
, связанных на расстоянии 
от точки подвеса невесомой пружиной жесткости 
– рисунок 37.5. На первый взгляд в качестве обобщенных координат естественно взять углы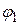 
и 
, которые маятники образуют с вертикалями черезх точки подвеса. Решение уравнений движения дает в этом случае следующий результат:
|
|
|
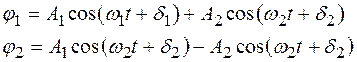. (37.12)
где 
- константы, определяемые начальными условиями, а собственные частоты определяются соотношениями:
. (37.13)
Одна из собственных частот определяется только длиной маятников, а вторая, кроме того, еще и жесткостью и местом закрепления пружины.
Легко видеть, что если в качестве обобщенных координат выбрать полусумму и полуразность и -
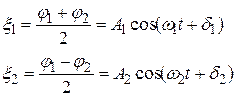, (37.14)
то получим новые обобщенные координаты 
и 
, каждая из которых изменяется по простому гармоническому закону. Эти координаты и есть нормальные обобщенные координаты системы в рассматриваемом случае.
Нормальные колебания системы представляют собой два частных случая колебаний, которые может совершать система. В одном случае маятники надо отклонить на одинаковые углы в одну сторону и одновременно отпустить. Система будет совершать колебание с частотой 
- маятники синфазно отклоняются от положения равновесия, пружина не играет никакой роли. В другом случае, для совершения колебания с частотой 
, маятники следует развести на одинаковые углы в противоположные стороны и одновременно отпустить. Маятники будут совершать противофазные колебания с частотой .
Рассмотрим систему из трех одинаковых шариков, соединенных одинаковыми пружинками. Такая система представляет собой фактически, очень примитивную, но все же модель одномерного кристалла. Если шарики могут двигаться только в плоскости рисунка, то такая система будет обладать тремя степенями свободы. Нормальные колебания такой системы показаны на рисунке 37.7. Очевидно, что такие же колебания можно представить происходящими в плоскости, перпендикулярной рисунку. Кроме того, можно представить колебания, соответствующие распространению в системе продольной волны - если шарики могут совершать колебания только вдоль линии соединяющей их. В этом случае тоже возможны три моды колебаний, при которых смещение из положения равновесия соответствует трем модам для распространения поперечной волны. Всего в трехмерном случае получаем 
возможных колебаний в соответствии с количеством степеней свободы шариков.
|
|
|
|
|
|
