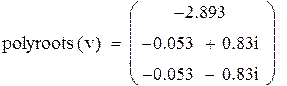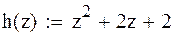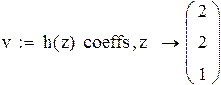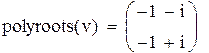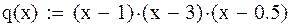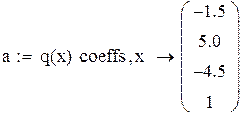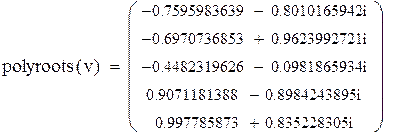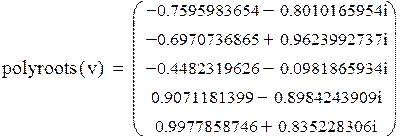|
1. Функция polyroots. Пример 1. Вектор-столбец коэффициентов: . 2. Оператор solve.
|
|
|
|
1. Функция polyroots.
Аргументом функции polyroots является вектор-столбец коэффициентов многочлена, корни которого требуется вычислить (начиная с коэффициента при нулевой степени).
Пример 1.
| Пусть требуется вычислить корни многочлена: |
|
|
|
|
| Вектор-столбец коэффициентов: |
|
|
Для формирования вектора коэффициентов удобно использовать оператор coeffs из палитры Symbolic.
Пример 2.
|
|
| Пусть требуется вычислить корни многочлена: |
|
|
| Сформируем вектор-столбец его коэффициентов: |
|
|
Подчеркнем, что оператор coeffs не нуждается в том, чтобы многочлен был записан в канонической форме. Если многочлен задан в форме сумм и произведений (см. пример 3 ), то оператор coeffs сам преобразует его к канонической форме и сформирует вектор коэффициентов.
Замечание. Для того, чтобы представить многочлен в канонической форме служит оператор collect из палитры Symbolic.
Пример 3.
| Пусть дан многочлен: |
|
|
| Построим вектор-столбец его коэффициентов: |
|
|
|
|
| Теперь представим многочлен q(x) в канонической форме: |
|
|
По умолчанию для поиска корней полинома используется метод ЛаГерра ( LaGuerre ), но функция polyroots может использовать также и метод матриц-компаньонов. Чтобы выбрать именно этот метод, поставьте курсор мыши на функцию polyroots и щелкните правой кнопкой мыши. Теперь вам достаточно выбрать пункт Companion Matrix из всплывающего меню. Какой из двух численных методов выбрать? Почему Mathcad отдает предпочтение методу LaGuerre, а не Companion Matrix? Теория численных методов не дает однозначного ответа на первый вопрос. В приведенных ниже примерах метод Companion Matrix демонстрирует более высокую точность, чем метод LaGuerre. Но это ничего не доказывает. Можно только отметить, что в силу ряда причин точность метода LaGuerre резко падает с возрастанием степени многочлена. Что касается второго вопроса, то, по-видимому, разработчики численного процессора Mathcad исходили из того, что метод LaGuerre имеет репутацию исключительно надежного метода счета. На наш взгляд, за исключением очень простых случаев, целесообразно вычислять корни двумя методами, а затем, подставив полученные значения корней в многочлен, оценить точность (см. пример 4 ).
|
|
|
Пример 4.
| Пусть дан многочлен: |
|
|
| Построим вектор-столбец его коэффициентов: |
|
|
| Используем вначале метод LaGuerre: |
| Теперь воспользуемся методом Companion Matrix: |
|
|
|
|
Заканчивая описание функции polyroots, отметим одно ее чрезвычайно важное свойство. Функция polyroots может вычислять корни многочленов с комплексными коэффициентами (см. пример 5 ).
| Пусть дан многочлен: |
|
|
Пример 5.
| Построим вектор-столбец его коэффициентов: |
|
|
| Используем вначале метод LaGuerre: |
|
|
| Теперь воспользуемся методом Companion Matrix: |
|
|
2. Оператор solve.
Оператор solve исключительно прост в использовании. Не требуется формировать вектор коэффициентов, достаточно записать многочлен (необязательно в канонической форме), а затем ввести оператор solve из палитры Symbolic.
Так как оператор solve работает с символьным процессором, необходимо учитывать, что, в зависимости от вида операнда, задача будет решаться точно или численным методом. Если вместе с оператором solve используется оператор float, символьный процессор использует численный метод.
Замечание. Если символьный процессор, получив инструкцию решить задачу точно, не смог найти решение, он, не прибегая к помощи численного процессора для поиска приближенного решения, выдаст сообщение “No solution found” (решение не найдено).
|
|
|
Оператор solve (если вместе с ним не используется оператор float ) даст указание символьному процессору найти корни уравнения точно, если все числа в многочлене записаны без десятичной точки. Кроме целых чисел в записи многочлена могут содержаться радикалы из целых положительных чисел, а также символы π и е.
Что понимает символьный процессор под точным определением корней? Очевидно, что в том случае, когда все корни уравнения рациональные числа, их следует вычислить без погрешности. Но, кроме этого, символьный процессор может записать корни в форме радикалов, а если это не удается, в форме тригонометрических выражений (см. пример 6 ).
|
|
|
|
|
|
|
|
|