Основные положения, выносимые на защиту 2 глава

Сравнение результатов, полученных при аппроксимации предложенным методом в случае моногармонического входного воздействия, с результатами, рассчитанными с помощью функций Берга, показало их полную адекватность. В отличие от модели Берга, предложенный метод аппроксимации позволяет получать аналитические выражения не только для АХ гармоник сигнала на выходе УО, но и АХ любых интермодуляционных компонентов при полигармоническом входном воздействии.

В нашем случае выражения для АХ УО, ХБ УО, ИХ УО, соответственно, имеют вид:

 

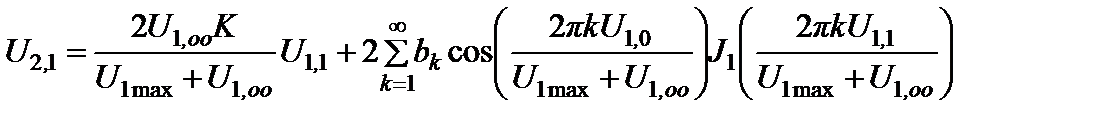. (18)

 

(19)

 

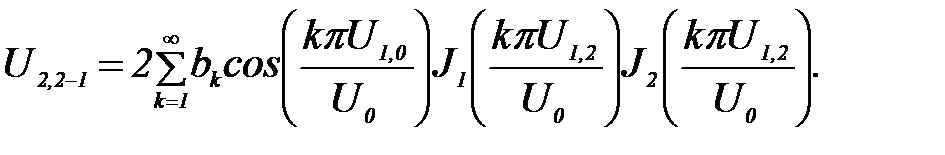(20)

 

Аналогичные выражения получены для идеального ограничителя при U_1,ог стремящемся к нулю.

Предложенным методом был исследован также смеситель частоты (СМ) с ПХ отличной от идеальной (квадратичной параболы).ПХ СМ, аппроксимированная выражением

 

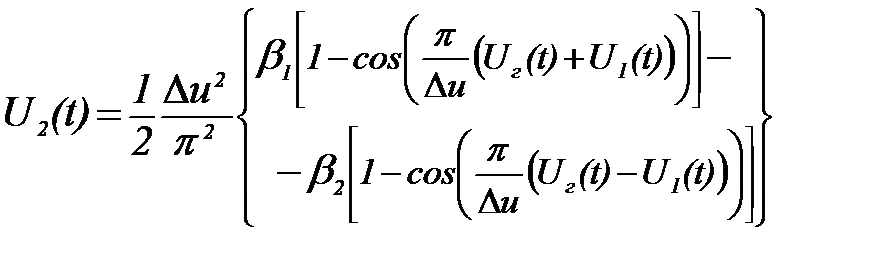, (21)

 

позволяет получить его основные характеристики. Здесь U _г(t) - колебание гетеродина, b ₁ и b ₂ - коэффициенты функций, аппроксимирующих ПХ СМ.

Получены аналитические выражения для АХ СМ, ХБ СМ и ИХ СМ:

 

, (22)

 

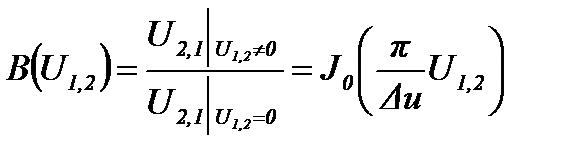, (23)

 

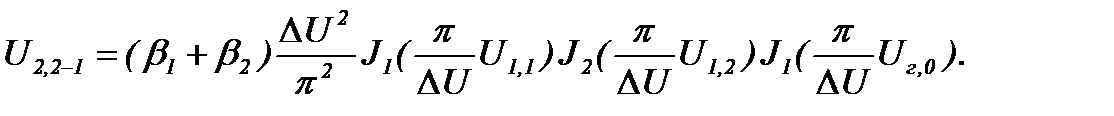, (24)

 

где U _г,о - амплитуда колебания гетеродина.

Из всех вышеприведенных примеров видна простота аналитических выражений для основных характеристик УТ, УО и СМ, которые, в отличие от полученных другими методами, дают возможность легко анализировать характер изменения функциональных зависимостей при изменении их аргументов.

В работе проведен анализ многокаскадного УТ РПУ и получены аналитические выражения для его основных характеристик. Исследован вопрос зависимости динамического диапазона УТ от числа содержащихся в нем усилительных каскадов.

Некоторые результаты, полученные с помощью предложенного метода аппроксимации комбинированными функциями ПХ идеальных УО и идеального смесителя, содержат ряды функций Бесселя, сходящиеся к заранее известным

значениям, полученным обычным путем. Это дает возможность определить пределы ранее неизвестных выражений для этих рядов, которые, возможно, могут иметь самостоятельное значение в отдельно взятых физико-математических приложениях. Имитационно-аналитическая модель трассовых испытаний РПУ учитывает всю совокупность аддитивных помех, которые попадают в полосу пропускания его ФПИ, и их взаимодействие на НЭ усилительного тракта как с сигналом, так и между собой. Если известна вероятность поражения канала связи станционной помехой, то их общее число М_i в i-м сеансе в заданной полосе Δf фильтра предварительной избирательности находится по закону Пуассона. Уровень напряжения j-й помехи U_пj определяется из предположения, что уровни станционных помех распределены по логарифмически-нормальному закону [75]. Уровни сигналов в различных сеансах связи также считаются распределенными по логарифмически-нормальному закону.

Законы замирания сигнала и помех принимаются релеевскими, райсовскими, односторонне-нормальными и др. с учетом статистики, приведенной, например, в [260]. Предполагается, что вдоль оси частот в пределах полосы пропускания фильтра предварительной избирательности станционные помехи распределены равномерно. В этом случае, с учетом формулы (12), уровень напряжения сигнала U_с(вых)(t) на выходе УТ РПУ описывается выражением

 

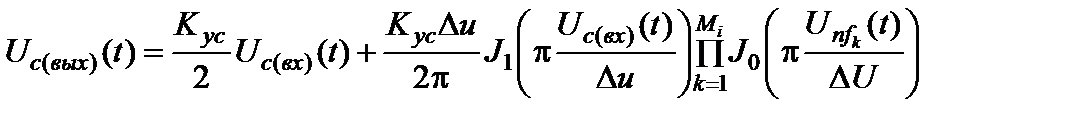. (25)

 

Одновременно на выходе УТ РПУ за счет взаимодействия станционных помех образуются интермодуляционные помехи нечетных порядков, часть из которых при выполнении условий (2 f _r - f _p) = f _c, (f _r + f _p - f _s) = f _c, 3 f _r - 2 f _p= f _c и т. д. попадает в ФОИ. Уровни интермодуляционных помех, например, третьего порядка определяются следующим образом:

, (26)

 

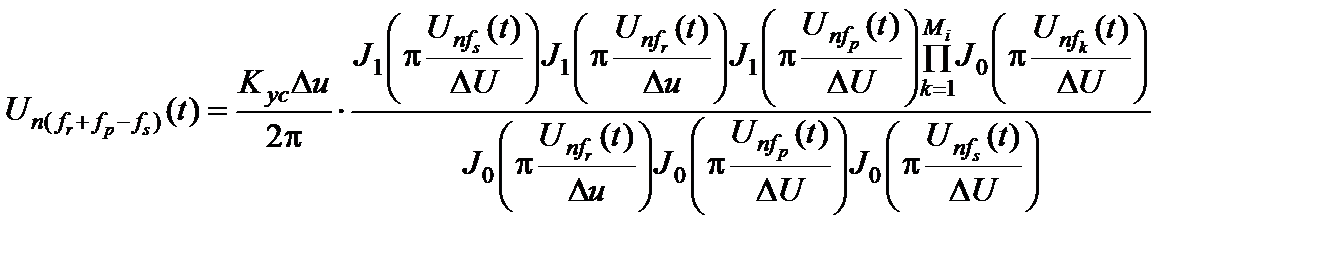. (27)

 

Определив уровень сигнала и все уровни интермодуляционных помех, которые попадают в полосу пропускания ФОИ, можно найти мощность этих помех как сумму их индивидуальных мощностей и рассчитать отношение сигнал/помеха H². Зная H², можно определить вероятность ошибочного приема элемента в любой заданный момент времени, построить вектор ошибок и определить число этих ошибок, обусловливающих качество сообщения, принятого в проводимом сеансе связи. Для коротких сеансов связи, когда длительность сообщения во много раз меньше интервала корреляции замирания сигнала и помех, оценку качества сеансов связи можно производить непосредственно по отношению сигнал/помеха H².

В третьей главе диссертации развиваются приложения метода аналитического моделирования (п. 1 положений, выносимых на защиту) в отношении цифровых РПУ (п. 2 положений, выносимых на защиту), в состав АЦП которых, наряду с дискретизаторами, входят квантователи. Квантователи - нелинейные элементы, и в связи с этим АЦП вносят определенные искажения в преобразуемые в цифровую форму сигналы. Предложенный метод аппроксимации ПХ НЭ комбинированными функциями является удобным инструментом для анализа работы квантователей в условиях большого количества помех, воздействующих на вход АЦП. Основные результаты третьей главы изложены в работах [92, 94, 121, 122, 124, 175, 232, 233] и в отчетах по НИР, проведенных под его руководством [120-124].

Передаточная характеристика квантователя описывается выражением:

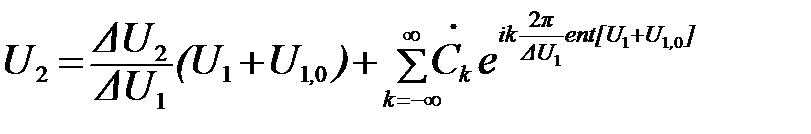, (28)

где 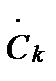- коэффициент комплексного ряда Фурье, в который разлагается пилообразная функция d U ₂ = U ₂ – U ₁D U ₂/D U ₁, D U ₁ - шаг квантования по входу, D U ₂ - шаг квантования по выходу, U ₁₀ - постоянное смещение (для квантователя с округлением U ₁₀ = 0).

Для квантователя с округлением АХ имеет следующий аналитический вид:

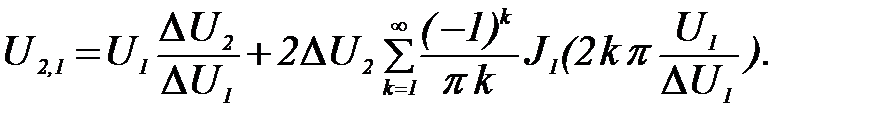(29)

При бигармоническом входном воздействии взаимная модуляция сигналов описывается выражением:

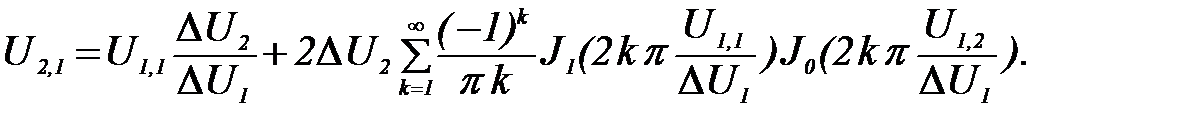(30)

Амплитуда интермодуляционного колебания третьего порядка в случае равноуровневого бигармонического входного воздействия описывается формулой:

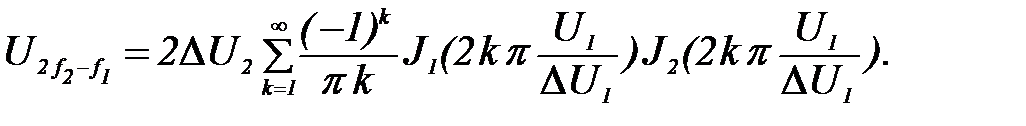(31)

Выражения, аналогичные вышеприведенным, получены и для квантователя с усечением.

В работе рассмотрены варианты моделей квантователей с ограниченным числом уровней и с неравномерным шагом квантования.

Результаты аналитического моделирования квантователя при увеличении числа членов в аппроксимирующем его ПХ ряде Фурье сходятся к результатам детерминированной модели квантователя [93] и результатам, полученным имитационным путем.

Предложенный метод аналитического моделирования ПХ квантователей дал возможность разработать модель трассовых испытаний цифровых РПУ и с помощью нее определить зависимость КИД КС от параметров устройства цифровой обработки сигнала [92].

Четвертая глава диссертации посвящена методу наклонного зондирования ионосферы широкополосными сигналами (п. 7 положений, выносимых на защиту), компьютерному имитационному методу моделирования двухмерного КС (п. 5 положений, выносимых на защиту), методу моделирования трехмерного ПВ КС (п. 6 положений, выносимых на защиту), методу физического моделирования КВ КС (п. 8 положений, выносимых на защиту) и методу моделирования трассовых испытаний КВ СС в условиях воздействия преднамеренных помех.

Описан метод наклонного зондирования ионосферы широкополосными сигналами,отличающийся возможностью одновременной регистрации огибающей импульсной реакции КВ КС и значений комплексных коэффициентов передачи отдельных лучей КВ канала связи как функций времени. На рис. 4.2.1 изображена блок-схема разработанного под непосредственным руководством автора диссертации измерительного комплекса, a на рис. 4.2.2 - 4.2.5 приведены фотография его внешнего вида и фотографии примеров регистрации исследуемых с помощью измерительного комплекса параметров отдельных лучей КВ канала связи. Новые технические решения в устройстве наклонного зондирования ионосферы широкополосными сигналами защищены двумя авторскими свидетельствами. Результаты исследования КВ КС, полученные с помощью измерительного комплекса были положены в основу разработанных имитационных математических и физических моделей.

Описана имитационная модель двухмерного многолучевого КС, учитывающая всевозможные аддитивные помехи и их взаимодействие друг с другом и с сигналом в УТ РПУ с заданными характеристиками [48, 172, 174, 175 ]. Вид аппроксимации ПХ РПУ при имитационном моделировании не является критическим. Важно обеспечить адекватность параметров УТ РПУ и аппроксимирующей его ПХ модели.

Описан новый метод имитационного компьютерного моделирования вектора напряженности электромагнитного поля в точке приема, позволяющий создать ПВ модель трехмерного сигнала с учетом тонкой структуры многолучевого КС и углов прихода индивидуальных лучей, а также с учетом характера поляризации электромагнитной волны в каждом отдельно взятом луче [ 172, 174, 175, 216, 218].

Этот метод позволяет при имитации трассовых испытаний учитывать влияние на надежность передачи сообщений параметров приемных антенн, сравнивать способы приема сигналов на разнесенные в пространстве и по поляризации антенны, оценивать эффективность функционирования компенсаторов станционных помех.

Дано описание различных методов имитационного физического моделирования КВ КС. Новой, отражающей творческий вклад автора в эту область, является физическая модель КВ КС с использованием реальных гармонических сигналов собственных или посторонних радиостанций, например, станций точного времени (метод “ЭКВИВАЛЕНТ”). Суть метода “ЭКВИВАЛЕНТ” заключается в том, что принимается гармонический сигнал (в нашем случае от станции точного времени), который отражает истинные замирания сигнала на данной трассе. Этот сигнал, используемый в качестве несущего колебания, подается с выхода ФОИ РПУ на промежуточной частоте на вход КВ возбудителя, манипулируется соответствующим способом и переизлучается на заданной частоте, на которую настроен рабочий приемник. На антенне этого приемника происходит суммирование переизлученного возбудителем сигнала с реальными аддитивными помехами, присутствующими на этой частоте. Таким образом, учитываются и реальные замирания сигнала, и реальные помехи в точке его приема. На метод физического моделирования трассовых испытаний КВ СС получено авторское свидетельство.

Кратко описан разработанный метод имитационного моделирования трассовых испытаний КВ СС в условиях воздействия преднамеренных помех. В модели функционируют три имитационных системы: канала передачи сообщений, средств радиоразведки противодействующей стороны и аппаратуры генерации преднамеренных помех. Предполагается, что преднамеренные помехи появляются только в случае, когда факт передачи сообщения обнаружен радиоразведкой противника. Считается, что радиоразведка противника находится преимущественно в менее выгодном положении по сравнению с каналом передачи сообщений, так как маловероятно, чтобы рабочие частоты, на которых ведется передача сообщения, являлись бы оптимальными для трассы "передатчик сообщений" –

"разведывательный приемник". Из этих же соображений маловероятно и то, чтобы между источником преднамеренных помех и приемником сообщений имел место случай наиболее благоприятный для распространения преднамеренной помехи на частоте передачи сообщения. Поэтому энергетическое преимущество имеется на стороне канала передачи сообщения. Тем не менее, результаты моделирования такого рода ситуации показали, что в условиях возможного противодействия радиосредств противника передавать сообщение следует мощностью, не превышающей уровень, который необходим для обеспечения удовлетворительного качества приема этого сообщения. Чрезмерное увеличение мощности передачи повышает вероятность обнаружения сигнала противоборствующей стороной и в результате появления преднамеренных помех на рабочей частоте коэффициент исправного действия канала связи не увеличивается с увеличением мощности сигнала, а с некоторого момента начинает уменьшаться. Отсюда следует вывод: передача сообщений с целью скрытности должна вестись предельно малой мощностью даже за счет снижения скорости манипуляции. Полученные выводы хорошо согласуются с современными требованиями к перспективным коротковолновым приемопередающим устройствам для Министерства обороны. “Перспективы развития военной КВ радиосвязи существуют в рамках создания и практического применения как в тактическом, так и высших звеньях управления парка портативных (маломощных) КВ радиостанций (Р_ПРД ≤ 1 … 10 Вт), имеющие узкие (Δf ≈ 10 … 50 Гц) и «сверхузкие» (Δf ≈ 2 … 10 Гц) полосы пропускания приемников" [58].

В пятой главе описаны методы повышения надежности КВ каналов связи, соответствующие п. 9 положений, выносимых на защиту, обоснованные автором с помощью математического и физического моделирования и проверенные в ходе натурных испытаний. Приведены результаты вычислительных экспериментов и натурных испытаний КВ систем связи, которые были проведены лично автором или под его непосредственным руководством. Эти результаты отражены в работах автора [47, 103, 104-107, 159-162, 169, 170, 171, 177-186, 193, 215, 251-255], а также в соответствующих отчетах по НИР и ОКР.

В главе приведены результаты трассовых сравнительных испытаний предложенной и разработанной под непосредственным руководством автора медленнодействующей системы связи ЧТ-20, имеющей скорость манипуляции 4 бода, с базовой системой ОФТ-500.

Полученные результаты показали, что за счет снижения скорости манипуляции, введения избыточного кодирования и частотно-временного разнесения мощность передатчика для КС с ЧТ-20 может быть уменьшена на 40 дБ по сравнению со штатным видом манипуляции ОФТ-500. При сохранении штатной мощности передатчика значительно увеличивался КИД КС с ЧТ-20, достигая значений близких к 100%.

Вычислительные эксперименты с использованием разработанных имитационно-аналитических моделей дискретных каналов связи для вышеуказанных систем показали практически те же самые результаты, что и трассовые испытания.

Результаты исследований позволяют сделать вывод об адекватности разработанных в диссертации математических моделей реальным КВ каналам связи.

Приведены результаты исследования надежности передачи сообщений с использованием метода “ЭКВИВАЛЕНТ” [115] для случая ретрансляции сообщений через удаленный ретрансляционный пункт. Показано, что разнесение по частоте, даже при отсутствии обратной связи, позволяет достичь значения КИД КВ КС при круглосуточной работе порядка 80¸90 %.

Результаты вычислительных экспериментов с использованием имитационно-аналитических моделей дискретных КС показали, что передачу сообщений в режиме ЧТ целесообразно производить с большой девиацией частоты. При этом прием сигналов на поднесущих частотах нужно осуществлять индивидуально, как прием двух АТ сигналов с автовыбором наиболее достоверных элементов [187]. Показано, что энергетический выигрыш при приеме ЧТ сигналов с большой базой как двух АТ, по сравнению с методом приема обычных ЧТ сигналов, достигает значений 10-30 дБ и более в зависимости от уровня надежности связи.

Результаты имитационно-аналитического моделирования трассовых испытаний УТ РПУ подтвердили большое влияние значений динамического диапазона РПУ и их чувствительности на надежность передачи сообщений. Было количественно оценено влияние загрузки КВ диапазона станционными помехами на ухудшение отношения сигнал/помеха. Так, например, при отсутствии адаптации по чувствительности РПУ с динамическим диапазоном 72 дБ при коэффициенте загрузки станционными помехами К = 0,3 энергетически проигрывает идеальному РПУ 11 дБ, а при К = 0,9 - соответственно 22 дБ. Наличие адаптации по чувствительности существенно уменьшает энергетические потери. Так, при К = 0,3 они составляет 1,2 дБ, а при К = 0,9 - соответственно 3 дБ. Таким образом, при наличии большого числа станционных помех введение адаптации РПУ по чувствительности позволяет получить энергетический выигрыш порядка 10¸20 дБ [129]. Энергетические потери в УТ РПУ более критичны к динамическому диапазону смесителей частоты, нежели к динамическому диапазону усилителей. Так, например, уменьшение динамического диапазона смесителя частоты на 1 дБ приводит к энергетическим потерям не на 1 дБ, как в случае с усилителем, а на 3 дБ [197].

Было проведено имитационно-аналитическое моделирование трассовых испытаний цифрового РПУ с использованием предложенной аналитической модели квантователя. Показано, что, если число шагов квантования равно или превышает значение 9 (для обеих полярностей напряжения) при полосе пропускания ФПИ равной 100 кГц, то при наличии регулируемого входного аттенюатора цифровое РПУ вынесенного приемного центра энергетически проигрывает идеальному не более 2 дБ, a при полосе пропускания ФПИ равной 40 кГц энергетический проигрыш у цифрового РПУ вообще отсутствует [92].

Последняя шестая глава посвящена основам проектирования, имеющей двойное применение высоконадежной системы континентальной КВ мобильной автоматической радиосвязи со свободным доступом пользователей, (п. 9 положений, выносимых на защиту) в которой используются КВ каналы передачи сообщений, разработанные на основе проведенных автором исследований. Основное

содержание главы опубликовано в работах [47, 103, 104-107, 159-162, 169, 170, 171, 177-186, 193, 215, 251-255, 282 ].

Основным способом повышения скрытности при сохранении надежности передачи сообщений является предельно возможное снижение скорости манипуляции, значение которой снизу ограничено скоростью изменения параметров коэффициента передачи КВ КС. С учетом возможного значения ухода частоты сигнала за счет явления Доплера, вызванного нестабильностью ионосферы и достигающего величины 1,5 Гц, электрическая скорость манипуляции может быть снижена до 4-х Бод. Положительным моментом при этом является то, что на низкой скорости передачи сообщений нивелируется явление многолучевости. Результаты приведенных в предыдущих главах исследований показали, что при принятии дополнительных мер повышения надежности связи (избыточное кодирование, адаптация приемного устройства к условиям связи, частотно-, пространственно-, территориально- и регионально-разнесенный прием сигналов и т. п.) результирующий энергетический выигрыш КС с ЧМ и низкой скоростью манипуляции (4 бода) по сравнению со случаем передачи сообщений на высокой скорости порядка 500 бод методом ОФМ может составить 40-60 дБ т. е. на низкой скорости передача может вестись без ухудшения надежности связи мощностью порядка 10 мВт – 1 Вт. Естественно, что обнаружить сигналы, передаваемые такой мощностью очень проблематично. Это нашло практическое подтверждение при эксплуатации принятого на вооружение изделия “Околыш” в условиях боевых действий.

Другая высоконадежная и одновременно скрытная система связи, разработанная под руководством автора диссертации была принята на вооружение ВМФ. Здесь также используется минимальная скорость манипуляции 4 Бода. Передача ведется мощностью порядка 1 Вт, что обеспечивает высокую скрытность передачи сообщений со стороны объекта. Одновременно предусмотрена

возможность работы в особо чрезвычайных ситуациях полной мощностью (10 кВт), что обеспечивает, как следует из результатов трассовых испытаний, приведенных в пятой главе, надежность связи близкую к 100%.

В шестой главе приведены аргументы в пользу того, что в России актуально создание автоматической КВ сети передачи данных со свободным доступом абонентов, в которой используются удаленные базовые ретрансляционные радиоцентры, интегрированные как с ССС, так и с другими системами связи (сотовыми, проводными и т. п.). В части использования вынесенных за пределы обслуживаемой зоны КВ ретрансляторов в диссертации развиты научно-технические концепции построения такого рода КВ сети связи, известные по работам Каменева Е. Ф., Головина О. В., Чистякова Н. И., Петровича Н. Т. [28, 85], Шарова А. Н. [265], Семисошенко М. А. [149] и других исследователей. В разработанном автором проекте для обслуживания территории всего евразийского континента необходимо 12 ретрансляторов, 9 из которых, как показано на рисунке 6.2.2, могут быть размещены на территории России.

Для работы всей системы требуется всего 12 номиналов рабочих частот с полосой пропускания по 12 кГц. Один ретранслятор способен обслуживать до 10 тыс. абонентов. В целом один комплект всего оборудования для евразийского континента рассчитан на общее число абонентов более, чем 100 тыс. Мощность передатчиков ретранслятора должна быть порядка 1 ¸ 10 кВт, а мощность подвижных радиостанций порядка 20 ¸ 200 Вт. Предусматривается носимый вариант абонентской аппаратуры, у которой мощность передатчика равна 1-2 Вт, и передача сообщений ведется с помощью антенны типа “наклонный луч”. Повышение помехоустойчивости передачи сообщений со стороны подвижного объекта в сторону ретранслятора достигается за счет предельно допустимого снижения скорости манипуляции. С учетом возможной скорости изменения параметров КВ канала связи, скорость манипуляции частоты несущего колебания на корреспондентском передатчике выбирается минимально допустимой и равной 4-5 бод. Манипуляция по частоте в корреспондентской радиостанции производится с большой девиацией (ЧТ-3000, ЧТ-6000 или ЧТ-9000). ЧТ сигналы на ретрансляторе

принимаются как два частотно-разнесенных сигнала АТ. Благодаря низкой скорости манипуляции спектры сигналов корреспондентских радиостанций на поднесущих частотах занимают предельно узкую полосу (порядка 10 Гц), что позволяет в одной боковой полосе частот телефонного канала связи за счет частотного уплотнения разместить более 100 индивидуальных АТ каналов.

Передача сообщений со стороны ретранслятора ведется в режиме уплотнения во времени со скоростью манипуляции равной 500¸1000 бит/с (ОФТ, ДОФТ). Таким образом, производится согласование пропускной способности каналов связи в сторону ретранслятора и от ретранслятора. Во время сеансов связи осуществляется адаптация к условиям связи по виду манипуляции (ОФТ и ДОФТ) со стороны ретранслятора. Информационные каналы связи совмещены с каналами управления. Для заказа абонентом КС используется частотно-временное кодирование, которое обеспечивает время вызова на связь в среднем равное порядка 30 с. Для оценки качества принятых фрагментов сообщения используются косвенные обобщенные методы оценки отношения сигнал/помеха по уровню напряжения на выходе ФНЧ детектора РПУ, оценке величины краевых искажений на выходе демодулятора и числу обнаруженных за счет избыточного кодирования знаков с ошибочно принятыми элементами. В случае низкого качества приема от корреспондента отдельных фрагментов сообщения эти фрагменты переспрашиваются базовым ретранслятором по каналу обратной связи. С целью выбора наиболее оптимального для передачи сообщения базового ретранслятора абонентские радиостанции осуществляют постоянное сканирование всех возможных каналов связи. Факт передачи сообщения удостоверяется базовым ретранслятором представлением передающей стороне квитанции о доставке сообщения адресату с указанием времени доставки.

Все основные технические решения построения высоконадежной автоматической КВ системы радиосвязи научно обоснованы с помощью разработанных автором моделей каналов связи, результатами физического моделирования и натурных испытаний.

В заключении освещены полученные в диссертации научные и практические результаты и указаны наиболее перспективные направления исследований в области математического моделирования каналов связи и повышения надежности передачи сообщений по КВ КС.

К диссертации прилагается диск с программами моделей одномерных и двухмерных каналов связи, разработанных лично автором диссертации

В приложении приведены алгоритмы моделирования КС и функционирования технических средств для высоконадежной мобильной автоматической системы радиосвязи с удаленными ретрансляторами, а также номограммы для определения частот побочных каналов приема, и полученные в диссертации новые формулы для некоторых рядов функций Бесселя.

 

 

1. МЕТОДЫ ИМИТАЦИОННО-АНАЛИТИЧЕСКОГО МОДЕЛИРОВАНИЯ ОДНОМЕРНЫХ КАНАЛОВ СВЯЗИ

 

1.1. Особенности имитационных математических моделей одномерных КС

Под одномерными КС будем понимать каналы, описываемые одной единственной функцией времени. Такой функцией может быть напряжение на выходе регенератора сигналов РПУ (модель дискретного КС без краевых искажений в сечении H рис. 1), напряжение на выходе триггера демодулятора (модель дискретного КС с краевыми искажениями в сечении G рис. 1), напряжение на выходе ФНЧ демодулятора (модель дискретно-непрерывного КС с выходом в сечении D рис. 1) или просто поток ошибок элементов (модель дискретного КС без краевых искажений).

Отличительной особенностью разработанных в диссертации математических моделей одномерных КС является имитационное представление как линейных искажений сигнала в среде распространения (многолучевость), так и воздействия аддитивных помех в точке приема сообщения. Структура разработанных имитационно-аналитических моделей КС фактически не отличается от структуры самого КС, а протекающие в нем процессы замираний сигнала и аддитивных помех описываются соответствующими временными функциями. Динамическое обновление зависящих от времени значений параметров моделей дискретных КС обусловливается интервалами автокорреляции протекающих в них случайных процессов, что позволяет обеспечивать высокое быстродействие их алгоритмов по сравнению с алгоритмами непрерывных каналов связи, в которых интервалы между отсчетами сигнала и помех обусловлены полосой пропускания частот КС. С учетом вышеизложенного, разработанные имитационные модели дискретных КС целесообразно называть имитационно-параметрическими моделями (ИПМ).

Необходимо отметить также то, что разработанные ИПМ одномерных КС отличаются тем, что позволяют проводить вычислительные эксперименты, имитирующие как лабораторные испытания по определению зависимости вероятности ошибки при передаче сообщений в каналах с переменными
параметрами, так и сравнительные трассовые испытания КС с определением КИД в зависимости от мощности передатчика.

При имитации процессов на выходе одномерных КС для определения отношения сигнал/помеха как функции времени и формирования потока ошибок требуется знание зависимости от времени только модулей векторов сигнала и помех и не используется информация об их фазах.

Для моделирования различных законов замирания сигнала (релеевского, райсовского, одностороннего нормального и т. д.) [75, 260] требуется формирование нормального двухмерного случайного процесса. Известно, что модуль вектора центрированного нормального процесса с некоррелированными равномощностными квадратурами имеет релеевское распределение, а модуль вектора такого рода не центрированного нормального процесса распределен по закону Райса (обобщенному закону Релея) [96, 21]. В первом случае имеет место двухпараметрическое распределение. Для него нужно задавать среднеквадратическое отклонение (СКО) процессов и их коэффициент автокорреляции. В этом же случае при абсолютной корреляции квадратур центрированного нормального процесса его модуль имеет одностороннее нормальное распределение. Во втором случае мы имеем при одинаковых математических ожиданиях (МО) квадратур трехпараметрическое нормальное распределение. В общем случае разных значений СКО, МО, коэффициентов автокорреляции квадратур и задании коэффициента их взаимной корреляции будет иметь место семипараметрическое двухмерное марковское нормальное распределение, позволяющее получать различные законы замираний сигнала, часть из которых хорошо аппроксимируется законом Накагами [69]. Скорость замираний сигнала обусловлена значениями коэффициентов автокорреляции r _ак квадратур нормального процесса. Таким образом, нормальный случайный процесс при моделировании замираний сигнала должен быть марковским, который имеет в общем случае семь параметров: два МО, два СКО, два коэффициента автокорреляции r_ак и коэффициент взаимной корреляции квадратур r_вк. В большинстве случаев достаточно брать МО, СКО и r_ак квадратур равными по
величине. Тогда будет иметь место четырехпараметрическое распределение марковского нормального процесса.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: