Основные положения, выносимые на защиту 4 глава

 

Рис. 1.3.2. Блок-схема имитационно-аналитической модели одномерного дискретного КС с переменными параметрами

 

 

Из рисунка 1.3.2 видно, что блок-схема модели включает в себя функциональные блоки, которые выдают соответствующие выходные данные, являющиеся либо окончательными, либо промежуточными, т. е. входными данными для соседних блоков.

Ниже описаны выдаваемые отдельными блоками выходные данные и алгоритмы их формирования.

Блок № 1 формирует сигнал S₂(m) на выходе КС с учетом подаваемого извне на его вход сигнала S₁(m) и потока ошибок B(m), формируемого блоком № 2. Алгоритм формирования сигнала S₂(m) следующий:

S₂(m) = |S₁(m) - B(m)|. (1.4.2)

Блок № 2 формирует поток ошибок элементов B(m) с учетом зависимости от времени вероятности ошибок P_ош(m), текущее значение которых поступает с выхода блока № 3. Алгоритм получения потока ошибок следующий:

B(m) = ent[R₂(m)+P_ош(m)]. (1.4.3)

Здесь ent[x] – целая часть числа x,

R₂(m) – случайные числа вспомогательного ГСЧ блока № 2.

В этом же блоке учитывается сдваивание ошибок, которое происходит в режиме ОФТ. В этом случае алгоритм формирования потока ошибок дополняется следующими операциями:

B(m)=|b(m) – b(m-1)|, (1.4.4)

b(m)=ent[R1(m)+P_{ош, фт}(m)], (1.4.5)

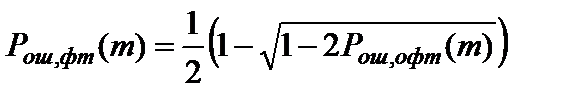, (1.4.6)

где Р_ошофт – вероятность ошибки элемента при приеме ОФТ сигналов; а Р _ошфт - вероятность ошибки элемента при приеме ФТ сигналов (в случае реализации этого режима работы).

Блок № 3 формирует значение вероятности ошибок элементов в соответствии с алгоритмом:

, (1.4.7)

где ; M = 4 для АТ, М = 2 для ЧТ и М = 1 для ОФТ,

H ²(m) – отношение энергии активного элемента сигнала к спектральной плотности мощности помех, k^* - коэффициент энергетических потерь в дБ.

Блок № 4 формирует значения отношений сигнал/помеха H ²(m) в соответствии с алгоритмом:

. (1.4.8)

Здесь V – скорость манипуляции [Бод],

ν²(m) – спектральная плотность мощности помех,

A₀(m) – амплитуда сигнала, поступающего на вход РПУ.

Блок № 5 формирует значение амплитуды сигнала A₀(m) в соответствии с алгоритмом:

,

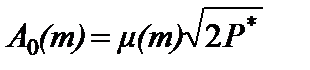где P^* - эквивалентная мощность сигнала, поступающая от передатчика с учетом коэффициентов усиления антенн на передающей и приемной стороне радиолинии,

μ(m) – коэффициент передачи КС.

Блок № 6 формирует значение эквивалентной мощности сигнала P^*:

P^*=P·G₁·G₂, (1.4.9)

где P – мощность передатчика [Вт],

G₁ – коэффициент усиления передающей антенны,

G₂ - коэффициент усиления приемной антенны.

Блок № 6 – конечный. Он не зависит от выходных данных других блоков.

Блок № 7 формирует коэффициент передачи КС μ (m), который изменяется во времени по случайному закону, соответствующему изменению модуля вектора двухмерного марковского нормального процесса:

, (1.4.10)

где μ_ср – значение СКО распределения коэффициента передачи;

q – значение МО квадратуры, нормированное в СКО;

r – коэффициент взаимной корреляции квадратурных компонентов двухмерного марковского нормального процесса, и - первообразующие нормированные и центрированные марковские нормальные процессы.

Блок № 8 формирует для очередного сеанса связи СКО параметра μ _ср в предположении, что оно распределено по логарифмически-нормальному закону (в дБ):

, (1.4.11)

где ,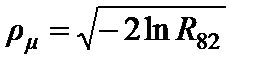

Здесь R ₈₁ и R ₈₂ – случайные числа от вспомогательного ГСЧ блока № 8,

μ _мо и μ _ско – МО и СКО параметра μ _ср.

Блок № 9 формирует первообразующие случайные марковские процессы и с помощью следующих рекуррентных уравнений:

, (1.4.12)

. (1.4.13)

Здесь - коэффициент автокорреляции процесса,

E_c(m) = ρ(m) cos (2πR₉₁(m)), E_s(m) = ρ(m) sin (2πR₉₁(m)),

,

τ – время корреляции замираний,

V – скорость манипуляции,

R₉₁(m) и R₉₂(m) – случайные числа, формируемые ГСЧ блока № 9.

Блок № 10 формирует значение спектральной плотности мощности помех, которая содержит компоненты, соответствующие атмосферному шуму и сигналам посторонних радиостанций:

ν²(m) = ν² _аш + ν² _сп (m), (1.4.14)

где ν² _аш – спектральная плотность мощности атмосферного шума,

ν² _сп спектральная плотность мощности станционных помех.

Блок № 11 определяет значение спектральной плотности мощности станционных помех с учетом вероятности их появления P _сп по следующему алгоритму:

, (1.4.15)

где P _сп – вероятность поражения КС станционной помехой,

R₁₁ – случайное число, генерируемое ГСЧ блока № 11,

μ _сп(m) – коэффициент замираний станционной помехи,

U _сп – средний уровень станционных помех в полосе частот Δf = 1 кГц.

Блок № 12 формирует уровни станционных помех, которые считаются распределенными по логарифмически-нормальному закону:

. (1.4.16)

Здесь ρ _сп = ,

R ₁₂₁ и R ₁₂₂ – случайные числа (поступают от ГСЧ блока № 12),

M _сп и Σ _сп соответственно МО и СКО логнормального закона распределения уровней станционных помех, задаваемых в дБ.

Блок № 13 определяет коэффициенты замираний станционных помех μ _сп(m) принимая закон их замираний релеевским. В этом случае:

, (1.4.17)

где 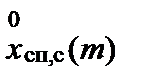и - первообразующие нормированные марковские нормальные процессы.

Блок № 14 формирует первообразующие процессы для коэффициента замираний станционных помех в предположении, что эти процессы марковские:

, (1.4.18)

. (1.4.19)

Здесь - коэффициент автокорреляции замираний станционных помех,

E _cп,с(m) = ρ _сп(m)cos(2 πR ₁₄₁(m)), E _сп,s(m) = ρ _сп(m)sin(2 πR ₁₄₁(m)),

,

τ _сп – время автокорреляции замираний станционных помех,

V – скорость манипуляции передаваемого сигнала, определяющая интервалы между отсчетами,

R₁₄₁(m) и R₁₄₂(m) – случайные числа, формируемые ГСЧ блока № 14.

Блок № 15 является вспомогательным ГСЧ, который определяет значения начальных случайных чисел для ГСЧ всех блоков, которые обусловлены единственным начальным числом R(0).

В приложении 4(В) дана блок-схема соответствующего алгоритма модели однолучевого дискретного канала связи с замираниями и станционными помехами. Соответствующая этому алгоритму программа “FEDING-1”, разработанная автором, приведена в приложении D-4.

Необходимо учитывать тот факт, что программа “FEDING-1” не отражает доплеровских эффектов, которые могут иметь место в реальном КВ канале связи, и поэтому результаты, получаемые для режима ОФТ, могут считаться корректными только при относительно высоких скоростях манипуляции (выше 250 бод).

Программа “FEDING-1” автоматически строит гистограммы законов замираний сигнала и сравнивает их с графиками, полученными аналитическим путем для частных случаев, релеевских, райсовских, односторонних нормальных или m-распределений.

Распределение Релея:

, (1.4.20)

где s_o = СKO × (10 ^0,05k) / (n );

СKO = A_cp × ,

A_cp - среднее значение амплитуды сигнала;

n² - спектральная плотность мощности шума;

k - коэффициент энергетических потерь, обусловленный неоптимальностью тракта аппаратуры;

V - скорость манипуляции.

Распределение Райса(обобщенное релеевское распределение):

, (1.4.21)

H_p = A_p × (10 ^0,05Ko) / (n ), (1.4.22)

где A_p - амплитуда регулярной составляющей сигнала;

I_o(х) - модифицированная функция Бесселя 1- го рода нулевого порядка.

Блок-схема алгоритма определения значений модифицированной функции Бесселя 1-го рода нулевого порядка приведена в приложении В.

Усеченное одностороннее нормальное распределение:

P(H)=0 для H<0 и

, для H > 0. (1.4.23)

Распределение Накагами (m-распределение) [67]:

, (1.4.24)

где Г(m) - гамма-функция, которая описывается выражением [18]:

Г(m) = (m > 0). (1.4.25)

Блок-схема алгоритма для определения значений гамма-функции c точностью до пятого знака при условии, что m < 50, приведена в приложении В. Этот алгоритм соответствует программе, опубликованной в [167].

Нужно заметить, что при m = 1 / 2 m-распределение вырождается в одностороннее нормальное распределение, а при m = 1 - соответственно в Релеевское распределение.

Изменяя входные параметры имитационной модели КС, можно проводить исследования зависимости потока ошибок от значений этих параметров. Если при этом начальное значение случайных чисел остается одним и тем же, то влияние за счет стохастичности процесса исключается. Так, например, при увеличении амплитуды сигнала уменьшается вероятность ошибок и, соответственно, их число в потоке ошибок. Местоположения правильно принятых элементов не меняются с увеличением амплитуды этого сигнала в последующих циклах испытаний, так как элементы, принятые правильно при меньшей амплитуде сигнала, при одном и том же значении начального случайного числа не могут быть принятыми ошибочно, когда амплитуда сигнала увеличивается. Этот факт позволяет в вычислительных экспериментах существенно экономить машинное время, так как нет необходимости при большей мощности сигнала проверять на наличие ошибок те местоположения, где они отсутствовали при меньшей мощности сигнала. Так как обычно исследуются каналы с малой вероятностью ошибок (порядка 0,1 - 0,001), то экономия машинного времени при повторных вычислениях составляет десятки и сотни раз. Для осуществления этой процедуры достаточно фиксировать значения случайных чисел, которые соответствуют местоположениям ошибочно принятых элементов при минимальных уровнях сигналов, или же в процессе проведения вычислительного эксперимента производить варьирование по всем заданным градациям уровня сигнала в те моменты времени, когда фиксируется ошибка.

1.5. Имитационно-аналитическое моделирование многолучевого дискретного КС без краевых искажений

Отличительной особенностью КВ КС является многолучевость, которая при высоких скоростях работы и обычных видах манипуляции ограничивает возможности повышения надежности связи за счет увеличения мощности передатчика. Если разность хода лучей превышает длительность отдельно взятого элемента, то в подавляющем большинстве случаев прием информации осуществляется по лучу, который имеет в данный момент времени наибольший уровень, а при переходе с одного луча на другой происходит рассинхронизация по
циклам, что может приводить к потере отдельных знаков сообщения. Многолучевость с большой разностью хода лучей приводит к интерференции элементов сообщения, приходящих в точку приема разными лучами, и без принятия специальных мер сигналы в лучах с меньшим уровнем играют роль аддитивных помех. Существуют специальные методы выделения отдельных лучей и организации разнесенного приема по лучам. Но эти методы в нижеописываемой модели не реализуются. Что касается обычных методов манипуляции при работе на относительно высоких скоростях, то они создают определенные проблемы перед разработчиками аппаратуры кодирования-декодирования (кодека), так как эта аппаратура в условиях многолучевости постоянно должна обеспечивать самосинхронизацию принимаемых знаков сообщения. Поэтому ГПОШ для многолучевого дискретного КС в качестве выходных данных должен выдавать, помимо вектора ошибок, еще и информацию об относительном времени задержки сообщения, которое само также является функцией времени. В многолучевой модели с помощью дискретной линии задержки с переключаемыми отводами одновременно с потоком ошибок имитируется изменение времени распространения сигнала при переходе с одного луча на другой, что на высоких скоростях манипуляции приводит к появлению “вставок” и “выпадений” элементов сообщений. На рисунке 1.5.1 изображена блок-схема такого рода модели.

ГПОШ

Принятое сообщение

Сумматор по модулю два

Блок управле- ния коммута- тором

Коммутатор отводов линии задержки

Дискретная линия задержки

Переданное сообщение

 

 

Рис. 1.5.1. Блок-схема модели многолучевого

дискретного канала связи

 

На рисунке 1.5.2 приведена блок-схема взаимодействия модели канала связи и модели кодека для случая многолучевости.

Обозначения, принятые на рисунке 1.5.2:

ИС - источник сообщения; ПС - получатель сообщения;

КУ - кодирующее устройство; ДКУ - декодирующее устройство; ЛЗ - линия задержки; К - коммутатор отводов линии задержки;

+

- сумматор “по модулю два”;

“FEDING - M” - модель многолучевого канала связи; а₁;...а_m - входные данные модели; S₁(n) - бинарная последовательность на выходе КУ; S₂(n) - бинарная последовательность на выходе решающего устройства приемника; dT - время задержки сигнала, приходящего основным лучом; B(n) - вектор ошибок.

Очевидно, что особые свойства многолучевого канала связи проявляются даже в наиболее простом случае двухлучевого канала связи, блок-схема обобщенного алгоритма модели которого приведена в приложении 4(В). В данной модели учитывается доля взаимного перекрытия элементов, приходящих в точку приема разными лучами. Поэтому с уменьшением скорости манипуляции многолучевость приводит к появлению краевых искажений элементов сообщения, и модель вырождается в однолучевой вариант, что имеет место и в реальном канале связи. Программа модели “FEDING-M” приведена в приложении D-8.

ИС

dT

“FEDING-M”

КУ

S1(n)

ЛЗ З

К

B(n)

аm

а1

S2(n)

ДКУ

к ПС

 

Рис. 1.5.2. Блок-схема взаимодействия модели канала связи и модели кодека для случая многолучевого канала связи

 

1.6. Имитационно-аналитическое моделирование дискретного канала связи с краевыми искажениями и дискретно-непрерывного канала связи

Модели дискретных каналов с краевыми искажениями и дроблениями (просечками) играют важную роль при разработке алгоритмов работы устройств, которые непосредственно подключаются к выходам демодуляторов радиоприемников телеграфных сигналов. Такими устройствами являются
регенераторы, устройства оценки качества, сложения разнесенных сигналов и т. д.

Краевые искажения подразделяются на три вида: случайные, регулярные и характеристические. Случайные краевые искажения являются следствием присутствия шумоподобных аддитивных помех. Регулярные краевые искажения обусловлены несовершенством передающих и приемных устройств, спецификой аддитивных помех, имеющих, например, при приеме ЧТ сигналов неравномерный спектр, эффектом Доплера, а также селективными замираниями сигнала в среде распространения. Причиной характеристических искажений являются переходные процессы в фильтрах приемных устройств. При передаче сообщений, представляющих собой случайные бинарные последовательности, характеристические искажения можно также считать случайными.

Если на интервале времени, соответствующем значению одного символа сообщения, под влиянием мешающих факторов происходит изменение этого значения с последующим возвратом к прежнему, то это явление называется дроблением элемента.

Краевые искажения и дробления обобщенно называют временными искажениями или телеграфными искажениями. Количественно краевые искажения оцениваются отношением модуля отклонения фронта элемента от его среднего местоположения Δt к длительности самого элемента T, выраженным в процентах:

d = 100 |Δt| / T. (1.6.1)

Исследователями широко используется модель краевых искажений, описываемых гауссовским законом распределения [1, 272]:

, (1.6.2)

где s - СКО случайной величины d.

Если имеет место закон распределения (1.6.2), то вероятность ошибки элемента сообщения описывается выражением

P_ош = 2 {[ 0,5 - Ф(m /s)] - [ 0,5 - Ф(m /s)]² }, (1.6.3)

где Ф (x) - интеграл вероятностей [18]; m - величина, характеризующая исправляющие способности регенератора.

Если s < 17 %, то можно оценивать вероятность ошибки с помощью упрощенного выражения

P_ош = 2 [ 0,5 - Ф(м/s)]. (1.6.4)

В каналах с переменными параметрами величина s зависит от времени. Однако вышеприведенная модель краевых искажений, являясь феноменологической, совершенно не отражает физику работы самого демодулятора. В частности, эта модель не дает представление о зависимости напряжения на выходе фильтра низких частот (ФНЧ) от отношения сигнал/помеха, что не позволяет, в свою очередь, исследовать явления зависимости дроблений от величины зоны нечувствительности решающего устройства (задержки по напряжению) и зависимости преобладаний от постоянного смещения на выходе ФНЧ. Это же замечание относится и к модели дроблений, предлагаемой в [272].

Ниже рассматривается лишенная вышеуказанных недостатков имитационная модель бинарной последовательности на выходе демодулятора, которая формирует краевые искажения элементов и дробления с учетом изменения параметров канала связи с течением времени. Квинтэссенция данного метода моделирования заключается в том, что интервал каждой элементарной посылки сообщения разбивается на N подынтервалов, которые в дальнейшем называются квантами. Зная отношение сигнал/помеха как функцию времени, можно определить поток ошибок для квантов, считая эти ошибки независимыми и происходящими с вероятностью, обусловленной как отношением сигнал/помеха, так и числом квантов, на которые разбиты элементы. Суммируя “по модулю два” полученный поток ошибок квантов с передаваемым сообщением и производя операцию скользящего суммирования на интервале длительности элемента вдоль всего сообщения, можно получить функцию времени, которая соответствует напряжению на выходе фильтра нижних частот демодулятора. Преобразуя полученное колебание с помощью порогового устройства, можно воспроизвести бинарную последовательность, которая
имитирует сигнал на выходе решающего устройства (триггера) демодулятора. Точность имитации по оси времени определяется числом N квантов на интервале одного элемента сообщения. Так как краевые искажения в трактах аппаратуры определяются обычно с точностью 1-5 %, то число N достаточно брать соответственно равным 101-21 (число N должно быть нечетным).

Функционирование модели, имитирующей краевые искажения, демонстрируется на рисунке 1.6.1.

Определим вероятность ошибки кванта Р_кв от отношения сигнал/помеха для заданного числа квантов на интервале одного элемента сообщения. Для этого рассмотрим канал связи с постоянными параметрами в условиях аддитивного белого шума. Предположим, что вероятность ошибки при приеме элементов сообщения равна Р_ош.

Представим каждый элемент сообщения в виде N равных частей-квантов. Полагаем, что на интервале каждого отдельно взятого кванта принимается индивидуальное независимое решение о его знаке с некоторой вероятностью ошибки Р_кв. Результирующее решение о значении отдельно взятых элементов выносится по совокупности решений о значениях, соответствующих этим элементам квантов. Ошибка при приеме элемента в этом случае должна происходить тогда, когда на интервале этого элемента число ошибочно принятых квантов будет превосходить заданный порог N_o. Вероятность ошибки элемента описывается соответствующей этому случаю формулой биномиального закона распределения вероятности

. (1.6.5)

Задача моделирования канала связи с временными искажениями в этом случае сводится к определению значения Р_кв при заданных значениях Р_ош, N и N_o. Для этого необходимо решить уравнение (1.6.5) относительно величины Р_кв. Точное аналитическое решение этой задачи неизвестно.

Будем искать приближенное решение в виде выражения, которое аналогично выражению (1.2.1) с той разницей, что введены поправочные коэффициенты К₁, К₂ и

К₃, которые обеспечивают точное решение уравнения (1.6.5) при любых трех заданных значениях Р_ош (или H).

. (1.6.6)

 

Окно скользящего сумматора

Ошибочно при-нятый элемент

(a) Переданное сообщение t

(b) Ошибки в квантах t

(c) Результат на выходе скользящего сумматора эквивалентный напряжению на выходе фильтра нижних частот

t

(d) Сигнал на выходе триггера t

(e) Стробирующие импульсы регенератора t

(f) Принятое сообщение на выходе регенератора t

 

 

 

Рис. 1.6.1. Формирование напряжения на выходе фильтра нижних частот и сигналов на выходах триггера демодулятора и регенератора

Естественно потребовать, чтобы N_o= (N-1)/2 и при отсутствии сигнала вероятность ошибки, определяемая по формуле (1.2.1), была бы равна 0,5. В этом случае и по формуле (1.6.6) при Н = 0 получаем значение коэффициента К₁ = 0,5.

Коэффициенты К₂ и К₃ находятся из системы уравнений:

Р_кв1 = 0,5 ехр(-К₃(ln(2Р_ош (Р_кв1)))^K₂; (1.6.7)

Р_кв2 = 0,5 ехр(-К₃(ln(2Р_ош (Р_кв2)))^K₂.

Решая эти уравнения, находим:

. (1.6.8)

Коэффициент К₃ можно найти зная либо Р_кв1, либо Р_кв2:

. (1.6.9)

Итак, задаваясь значениями N, P_кв1 и Р_кв2 и определяя по формуле (1.6.5) соответствующие значения Р_ош (N, P_ош1) и Р_ош(N, Р_ош2), можно с помощью выражений (1.6.8) и (1.6.9) определить коэффициенты К₂ и К₃. С целью предоставления возможности проведения расчетов при больших значениях N целесообразно вычисления проводить в логарифмическом масштабе, заменяя операции умножения и деления в соответствующих вычислительных алгоритмах на операции сложения и вычитания. В этом случае

. (1.6.10)

В табл. 1.6.1 приведены значения коэффициентов К₂ и К₃ для различных значений N при значениях Р_кв1 =0,2 и Р_кв2 =0,3.

Таблица 1.6.1

Значения коэффициентов К₂ и К₃

N = 1 N = 5 N = 11 N = 21 N = 51 N = 101

K₂ 1 0,89290448 0,82734569 0,77609359 0,7175291 0,684297

K₃ 1 0,46152849 0,30637636 0,22110829 0,1428717 0,101796

Таким образом, задаваясь числом квантов N, на которое разбиты элементы сообщения, и значением вероятности ошибки элементов Р_ош (или значением отношения сигнал/шум H) и определив коэффициенты К₂ и К₃ с помощью формулы (1.6.7), можно найти вероятность ошибки квантов Р_кв. На рисунке 1.6.2 приведены зависимости вероятности ошибки квантов Р_кв от вероятности ошибки элементов Р_ош и числа квантов в элементе N.

Р кв

0,5 0,1 0,01 0,001 0,0001 0,00001 Р ош

0,2

0,1

0,05

0,02

0,01

0,005

0,002

N = 11

N = 5

N = 1

N = 101

N = 51

N = 21

0,001

Рис. 1.6.2. Зависимости вероятности ошибки квантов от вероятности ошибки элементов и числа квантов в элементе

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: