 |
Основные положения, выносимые на защиту 6 глава
|
|
|
|
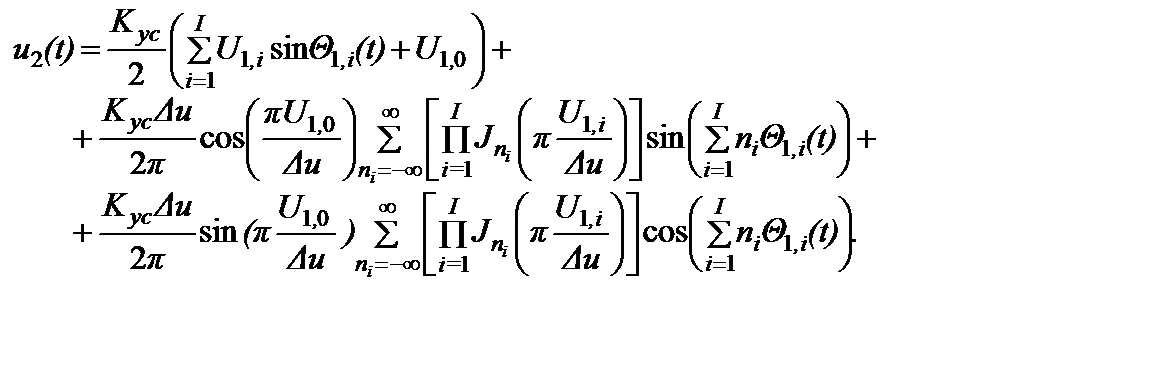 (2.3.2)
(2.3.2)
Из этого выражения следует, что в результате взаимодействия отдельных гармонических составляющих спектра входного колебания на НЭ ГТ РПУ на его выходе образуются гармоники и интермодуляционные составляющие сколь угодно высоких порядков. Первый член суммы (2.3.2) содержит транслируемый через ГТ на его выход спектр входного колебания за счет линейной составляющей ПХ с коэффициентом передачи K ус/2 без каких бы то ни было искажений. Второй член этой суммы содержит гармоники и интермодуляционные составляющие нечетных порядков (включая первый), а третий член – гармоники и интермодуляционные составляющие четных порядков. Из выражения (2.3.2) видно, что амплитуды интермодуляционных составляющих нечетного порядка, превышающего первый, т. е. когда n1 + n2 +…+ nI = 2m + 1 для m ≥ 1, определяются по формуле:
 , (2.3.3)
, (2.3.3)
а амплитуды интермодуляционных составляющих четного порядка, когда
n1 + n2 +…+ nI = 2m для m ≥ 1- по формуле:
 . (2.3.4)
. (2.3.4)
Из этих уравнений следует, что при U 1,0 = 0 на выходе ГТ будут отсутствовать интермодуляционные составляющие четных, а при U 1,0 = Δ u /2 - нечетных порядков.
Таким образом, при представлении ПХ ГТ РПУ в виде выражения (2.2.2) для известных параметров модели K ус и ∆ u можно с помощью выражений (2.3.3) и (2.3.4) определить значение амплитуды интермодуляционной составляющей спектра колебания любого заданного порядка на выходе ГТ.
Как уже говорилось, совокупный уровень всех компонентов входного воздействия не должен превышать максимально допустимое значение ∆u, т. е. всегда должно выполняться неравенство
 .
.
Если входное воздействие является моногармоническим, то для амплитудной характеристики ГТ РПУ из (5) можно получить выражение
|
|
|
 . (2.3.5)
. (2.3.5)
В таблице 2.3.1 даны результаты расчета амплитудных характеристик усилительного каскада с нелинейной характеристикой вида (2.2.2) при различных начальных смещениях рабочей точки U 10. Параметры усилителя имеют следующие значения:
- коэффициент усиления К = 10;
- порог ограничения по выходу U ог = 10 В,
- D U =2 U ог/ K = 2 B.
| АМПЛИТУДНАЯ ХАРАКТЕРИСТИКА УСИЛИТЕЛЯ Смещение Входное Аналитическое Имитационное раб. точки воздействие моделирование моделирование U 1,0 B U 1,1 B U 2,1 B U 2,1 B 0 0,01 0,09999846 0,09999843 0 0,1 0,9984595 0,9984592 0 0,5 4,812126 4,812124 0 1 8,608514 8,608511 0 1,5 10,86925 10,86925 0 2 11,81192 11,81191 0 2,5 12,25901 12,25901 1 0,01 0,04999999 0,04999993 1 0,1 0, 5 0,4999998 1 0,5 2,5 2,499999 1 1 5 4,999998 1 1,5 7,5 7,499998 2 0,01 1,539232Е-06 1,529185Е-06 2 0,1 0,001540547 0,001540546 2 0,5 0,1878744 0,1878744 |
Здесь же приведены результаты вычислительного эксперимента, проведенного с помощью имитационной модели, использующей для определения амплитуды спектральных составляющих быстрое преобразование Фурье. Имитационная модель обеспечивала 40 выборок на одном периоде колебаний, что позволило учесть влияние 20-й гармоники в спектре выходного колебания.
Из вышеприведенной таблицы видно, что аналитическое и имитационное моделирование дают практически полностью совпадающие результаты на всем рабочем участке нелинейной характеристики.
На рисунке 2.3.2 изображено семейство соответствующих таблице амплитудных характеристик.
При бигармоническом входном воздействии амплитуда выходного сигнала U 2,1 описывается выражением
 ,
,
которое свидетельствует о том, что в ГТ из-за нелинейных явлений происходит взаимная модуляция сигналов.
| U 10+ U 1,1<2,5 В |
| 0 0,5 1,0 1,5 2,0 2,5 U 1,1 В |
| U 2,1 В |
| U 10=0 |
| U 10=2 |
| U 10=1 |
Рис. 2.3.2. Амплитудные характеристики нелинейного
усилительного тракта
Используя последнее равенство, можно получить характеристику блокирования B(U 1,2), которая показывает степень подавления малого сигнала U 1,1 << Δ u превосходящим его по уровню сигналом U 1,2, и имеет следующий вид:
|
|
|

Из этого отношения следует, что при U 1,0 = Δ u /2 блокирование в ГТ РПУ будет отсутствовать. Но при этом максимально допустимый уровень входного воздействия уменьшается в два раза, и в два раза уменьшается коэффициент усиления ГТ.
В таблице 2.3.2 даны результаты расчета характеристик блокирования усилительного каскада с нелинейной характеристикой вида (2.2.2) при различных начальных смещениях рабочей точки U 10. Параметры усилителя имеют те же значения, что и в предыдущем случае (К = 10; U ог = 10В). Здесь же приведены результаты вычислительного эксперимента, проведенного с помощью имитационной модели. Имитационная модель обеспечивала 20 выборок на одном периоде колебаний с наибольшей частотой, что позволило учесть влияние 10-й гармоники этого колебания в спектре сигнала на выходе усилителя. Результаты аналитического и имитационного моделирования совпадают с точностью до четвертой значащей цифры.
На рисунке 2.3.3 приведено соответствующее семейство характеристик блокирования усилительного каскада.
Амплитуды интермодуляционных составляющих третьего порядка в спектре выходного колебания, которые используются для определения динамического диапазона ГТ, описываются выражением:
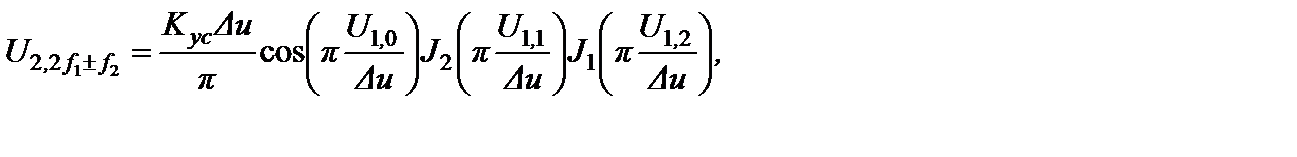 (2.3.6)
(2.3.6)
В таблице 2.3.3 даны результаты расчета интермодуляционных характеристик усилительного каскада с нелинейной характеристикой вида (2.2.2) при различных начальных смещениях рабочей точки U 10.
| U 10+ U 1,2 < 2,5 |
| U 10=1.5 |
| U 10=1 |
| U 10=0 |
| В 1.4 1.2 1.0 0.8 0.6 0.4 0.2 |
| 0 0,5 1,0 1,5 2,0 2.5 U 1,2 В |
Рис. 2.3.3. Характеристики блокирования нелинейного
усилительного каскада
| ХАРАКТЕРИСТИКА БЛОКИРОВАНИЯ УСИЛИТЕЛЯ Смещение Блокирующее Аналитическое Имитационное раб. точки колебание моделирование моделирование U 1,0 B U 1,2 B B(U 1,2) B(U 1,2) 0 0,5 0.9258159 0.9258048 0 1 0.7360006 0.7359953 0 1.5 0.5127477 0.5127516 0 2 0.3478789 0.3478881 0 2,5 0.2995263 0.2995364 1 0.5 1 1 1 1 1 1 1 1.5 1 1 2 0,5 1.358192 1.358159 2 1.0 2.274702 2.274579 |
| ИНТЕРМОДУЛЯЦИОННАЯ ХАРАКТЕРИСТИКА УСИЛИТЕЛЯ Смещение Амплитуды Аналитическое Имитационное раб. точки вх. колебаний моделирование моделирование U 1,0 B U 1,2 B U 2 (2fi - fj) B U 2 (2fi - fj) B 0 0,01 1.542047E-06 1.534548Е-06 0 0.02 1.233447E-05 1.232209Е-05 0 0.04 9.86149Е-05 9.858814Е-05 0 0.1 1.534216Е-03 1.534149Е-03 0 0.25 2.333194Е-02 2.333168Е-02 0 0.5 0.16929 0.1692786 0 1.0 0.9010519 0.9001743 0 1.25 1.269748 1.267067 1 0.25 1.019872Е-09 1.818884Е-07 1 0.5 7.399899Е-09 2.988677Е-07 1 0.75 2.11475Е-08 4.364015Е-07 1.5 0.1 1.084854Е-03 1.084841Е-03 1.5 0.2 8.545752Е-03 8.545812Е-03 1.5 0.4 6.424318Е-02 6.424146Е-02 1.5 0.5 0.1197061 0.1196883 |
|
|
|
Параметры усилителя имеют те же значения, что и ранее. В этой же таблице приведены результаты вычислительного эксперимента, проведенного с помощью имитационной модели.
На рис. 2.3.4 приведено соответствующее семейство интермодуляционных характеристик 3-го порядка.
Анализ полученных аналитическим и имитационным путем результатов показывает, что они отличаются не более, чем на 0,5%, а в подавляющем числе случаев относительная погрешность не превышает значения 0,0001. Существенное расхождение данных, полученных при смещении 1В, объясняется тем, что теоретическое значение амплитуд должно быть равно нулю (cos(p/2)=0), а имитационная и аналитическая модели имеют различные пороги чувствительности. Важно отметить факт отсутствия не только интермодуляций третьего порядка при смещении равном 1В, но и отсутствие блокирования при этом смещении. Однако необходимо иметь в виду, что при этом смещении, как уже говорилось,
коэффициент усиления уменьшается в два раза, а также, соответственно, уменьшается и максимально допустимое напряжение на входе усилителя. Участок интермодуляционной характеристики для малых значений сигналов на входе усилителя при отсутствии смещения дан на рисунке 2.3.4 в увеличенном масштабе в виде пунктирной линии, которая очень хорошо подтверждают известный теоретический факт, что зависимость амплитуды интермодуляционной составляющей третьего порядка от уровня входных сигналов описывается параболой третьей степени.
Полученные результаты свидетельствуют, что относительно простое двухпараметрическое выражение (2.2.2), которое представляет собой сумму линейной функции и синусоиды, может служить аналитической моделью ГТ РПУ.
Отличительной особенностью предложенной модели является ее относительная простота при одновременном удовлетворении самого важного требования: возможности определения с помощью компактных выражений (2.3.3) и (2.3.4) параметров любой составляющей спектра колебания на выходе ГТ при сколь угодно большом числе входных воздействий и любом их уровне (в пределах допустимых значений).
|
|
|
| U 2f1-f2 1.4 1.2 1.0 0.8 0.6 0.4 0.2 |
| U 1,1+ U 1,2<2,5 |
| U 10=1 |
| U 10=1,5 |
| U 10=0 |
| 0 0.25 0.5 0.75 1.0 1.25 U 1,1 0 5∙10-310-2 2∙10-2 U1,2 |
| 1.23∙10-5 |
| 1.53∙10-6 |
Рис. 2.3.4. Интермодуляционные характеристики нелинейного усилительного радиоприемного тракта
2.4. Синтез проходной характеристики главного тракта радиоприемного
устройства по его параметрам
Для синтеза обобщенной ПХ ГТ РПУ необходимо определить значение параметра аппроксимации ∆ u, которое зависит от динамического диапазона D ГТ.
Динамический диапазон D обычно определяется как отношение амплитуды одного из двух входных сигналов при равноуровневом бигармоническом входном воздействии (U 1,1 = U 1,2 = U) к амплитуде интермодуляции третьего порядка вида (2 f 1 – f 2), порожденной при этом за счет нелинейности ГТ РПУ, когда пересчитанный на вход ГТ ее уровень равен 1мкВ.
В соответствии с выражением (2.3.6) амплитуда интермодуляции третьего порядка при отсутствии начального смещения рабочей точки (U 1,0 = 0) определяется по формуле:
 (2.4.1)
(2.4.1)
Известно представление функций Бесселя первого рода степенными рядами [81]:

В таком случае, при U << ∆ u в первом приближении можно считать, что

а 
Тогда из выражения (2.4.1) следует приблизительное равенство
 (2.4.2)
(2.4.2)
Разделив вычисленное с помощью выражения (2.4.2) значение амплитуды интермодуляционной составляющей третьего порядка на коэффициент усиления Кус, в
соответствии с методикой определения динамического диапазона приравняем полученный результат к 1 мкВ:
 (2.4.3)
(2.4.3)
Из выражения (2.4.3) определяем искомое значение параметра аппроксимации ∆ u:

Как правило, динамический диапазон ГТ РПУ D задается в децибелах:
 .
.
В этом случае  , и можно записать окончательное выражение для определения ∆ u через значение динамического диапазона D, заданного в децибелах:
, и можно записать окончательное выражение для определения ∆ u через значение динамического диапазона D, заданного в децибелах:
 (2.4.4)
(2.4.4)
Таким образом, параметры аналитической модели K ус и Δ u найдены, т. е. задача синтеза аналитической модели ГТ РПУ вида (2.2.2) по его основным характеристикам (коэффициенту усиления и динамическому диапазону) полностью решена.
В таблице 2.4.1 приведены результаты расчетов с помощью выражения (2.4.4) значений величины D u в зависимости от значений динамического диапазона D дБ.
Таблица 2.4.1
| D дБ | |||||
| D u [B] | 0,025 | 0,14 | 0,785 | 4,42 | 24,8 |
|
|
|
Проверим адекватность синтезированной модели посредством сравнения результатов расчетов ее АХ, ХБ и ИХ с результатами оригинала, у которого проходная характеристика имеет вид arctg(x), а АХ, ХБ и ИХ получены имитационным путем.
В модели (2.2.2) определению подлежит только параметр ∆ u, т. к. параметр K задается в качестве параметра усилителя как коэффициент усиления.
Параметры усилителя:
K = 10, D = 81,34 дБ (это соответствует порогу ограничения 10 В).
В результате вычисления получено значение ∆ u = 1,0054 В.
Для синтеза характеристики использовано всего 2% интервала допустимых значений входного сигнала (20 мВ), т. к. 1 мкВ пересчитанного к входу усилителя значения интермодуляции третьего порядка реализуется при 10 мВ каждого из компонентов равноуровневого бигармонического входного воздействия.
Результаты расчета характеристик приведены в таблице 2.4.2.
Таблица 2.4.2
| U вх | АХatn | АХанмод | ε % | ХБatn | ХБанмод | ε % | ИХatn | ИХанмод | ε % |
| 0.1 | 0.9939 | 0.99072 | 0.32 | 0.988 | 0.988 | 0.02 | 0.00588 | 0.00594 | |
| 0.25 | 2.42 | 2.4038 | 0.67 | 0.093 | 0.0926 | 0.37 | 0.074 | 0.0836 | |
| 0.5 | 4.4023 | 4.308 | 2.14 | 0.0786 | 0.0738 | 0.35/0.32 | 0.4476 | ||
| 0.75 | 5.89 | 5.448 | 7.5 | 0.0647 | 0.0516 | 0.7/0.6 | - | - | |
| 6.9879 | 5.929 | 15.2 | 0.0537 | 0.035 | 1/0.84 | - | - |
Анализируя полученные данные, можно сделать заключение, что в пределах заданного динамического диапазона характеристики оригинала и аналитической модели совпадают с точностью не хуже, чем 1%.
Значительные расхождения характеристик, которые доходят, например, до 35% у характеристики блокирования, происходят за пределами рабочих значений входного воздействия. Однако качественно характеристики оригинала и модели мало отличаются во всей области практически возможных значений входных сигналов.
На рисунках 2.4.1(а), 2.4.1(б) и 2.4.1(в) приведены соответственно АХ, ХБ и ИХ для оригинала (сплошные линии) и аналитической модели (пунктирная линия).
| а |
| Uвых |
| 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Uвх |
| б |
| 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Uвх |
| B 0.5 |
| 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Uвх |
| в |
| Uвых 0.5 |
| 2f1-f2 |
| 2f2-f1 |
Рис. 2.4.1. Амплитудная характеристика (а), характеристика
блокирования (б) и интермодуляционная характеристика (в)
оригинала и аналитической модели ГТ РПУ.
Двухпроцентный рабочий интервал на рисунках отмечен вертикально вытянутым прямоугольником серого цвета. Из таблицы 2.4.2 и рисунков видно, что по отношению к рабочему интервалу имеется более чем десятикратный запас по уровню изменения входного напряжения, когда относительная ошибка для АХ не превышает значения 0.25%, для ХБ – 3.7% и для ИХ -13%.
Таким образом, для синтеза модели ГТ РПУ вида (2.2.2) достаточно знаний всего двух всегда известных характеристик: коэффициента усиления и динамического диапазона ГТ.
2.5. Модель многокаскадного усилительного тракта
Радиоприемные устройства, как правило, состоят из достаточно большого числа последовательно включенных друг за другом усилительных каскадов. В этом случае требуется последовательное преобразование входных воздействий, которое можно осуществить на рекурсивной модели, число итераций в которой определяется числом усилительных каскадов в тракте. Пусть тракт радиоприемного устройства представляет собой N последовательно включенных резонансных усилительных каскадов с ПХ НЭ вида (2.2.2). Рассмотрим основные характеристики такого тракта.
Для получения амплитудной характеристики достаточно моногармонического воздействия на вход тракта. При этом амплитуда колебания на выходе N-го каскада описывается рекуррентной формулой
 (2.5.1)
(2.5.1)
где K N - коэффициент усиления N-го каскада,
D U N - параметр, обусловливающий динамический диапазон N-го каскада.
На рисунке 2.5.1 показана зависимость амплитудной характеристики тракта, состоящего из N идентичных усилительных каскадов (К =2; D u =1). Точками на рисунке нанесены результаты, полученные с помощью имитационного моделирования.
Из приведенного рисунка видно, что с увеличением числа последовательно включенных в тракт усилительных каскадов резко сокращается участок характеристики, соответствующий линейной зависимости уровня выходного колебания от уровня входного. При числе последовательно включенных каскадов равном шести доля линейного участка составляет менее 3% общего створа характеристики. Каждый дополнительно включенный каскад уменьшает линейную часть характеристики в 2 раза. Таким образом, увеличивая число последовательно включенных усилительных каскадов, можно получить характеристику сколь угодно близкую к характеристике идеального ограничителя.
| N=6 |
| N=5 |
| N=3 |
| N=4 |
| N=2 |
| N=1 |
| U 2,1 ∆ u |
| 1,5 1,0 0,5 |
| 0 0,5 1,0 1,5 |
| U 1,1 ∆ u |
Рис. 2.5.1. Зависимость амплитудной характеристики от числа усилительных
каскадов в тракте (К = 2)
Значительно более сложным является описание характеристик, требующих бигармонического воздействия. Предположим, что резонансные цепи тракта отфильтровывают все нелинейные продукты на выходе каждого усилительного каскада, за исключением интермодуляционных составляющих третьего порядка вида U(2f2-f1). В этом случае на выходе усилительного каскада имеют место четыре гармонических колебания: два основных и два интермодуляционных. Каждый из этих четырех компонентов при прохождении через усилительный каскад влияет на уровни всех остальных компонентов. Учитывая симметричность математических
выражений по отношению к основным и интермодуляционным колебаниям, запишем только два из четырех уравнений, описывающих амплитуды этих колебаний. При этом будем иметь в виду тот факт, что уровни интермодуляционных составляющих спектра значительно меньше уровней основных колебаний сигнала. С учетом вышесказанного, ограничимся результатами взаимодействия компонентов, воздействующих на НЭ, содержащих только первые гармоники интермодуляционных колебаний, в то время как для основных колебаний учтем гармоники третьего порядка. В результате будем иметь следующие рекуррентные уравнения:
 (2.5.2)
(2.5.2)
 (2.5.3)
(2.5.3)
где U 2,1(0) = U 1,1; U 2,2(0) = U 1,2; U (2f1-f2)(0) = U (2f2-f1)(0) = 0.
При исследовании влияния блокирования бигармоническое воздействие является существенно разноуровневым, т. е. выполняется неравенство U 1,1 << U 1,2. В этом случае выражения (2.5.2) и (2.5.3) значительно упрощаются, и отдельные компоненты сигналов на выходе многокаскадного усилителя можно записать в следующем виде:
 (2.5.4)
(2.5.4)
 (2.5.5)
(2.5.5)
 (2.5.6)
(2.5.6)
U 2,1(0) = U 1,1; U 2,2(0) = U 1,2; U (2f2-f1)(0) = 0.
Характеристика блокирования может быть определена с помощью выражения
 (2.5.7)
(2.5.7)
В частном случае идентичных усилительных каскадов:
 (2.5.8)
(2.5.8)
На рисунке 2.5.2 показаны зависимости характеристик блокирования от числа усилительных каскадов в тракте.
Из рисунка видно, что увеличение числа усилительных каскадов в тракте приводит к резкому подавлению меньшего колебания большим. Точками на рисунке показаны результаты, полученные с помощью имитационной модели.
Представляет интерес сравнить амплитуды интермодуляционной составляющей третьего порядка и основного колебания меньшего уровня. На рисунке 2.5.3 приведены зависимости их отношений от уровня блокирующего сигнала и числа усилительных каскадов в тракте.
| N=1 |
| N=2 |
| N=3 |
| N=4 |
| N=5 |
| N=6 |
| U 2,2 KU 1,2 |
| 1,0 |
| 0,5 |
| 0,5 |
| 1,0 |
| U 1,2 ∆ u |
Рис. 2.5.2. Зависимость характеристики блокирования от числа усилительных
каскадов в тракте
Из рисунка видно, что, начиная с N = 4, в режиме глубокого ограничения сигналов амплитуда интермодуляционного колебания и основного колебания меньшего уровня становятся равными. Это явление наблюдается и в реальных усилительных трактах при глубоком ограничении входных воздействий.
Рассмотрим зависимость динамического диапазона тракта от числа содержащихся в нем усилительных каскадов. Воспользуемся методикой определения динамического диапазона по отношению уровня одного из основных сигналов в случае бигармонического равноуровневого входного воздействия к уровню интермодуляции вида U (2f2-f1)(N), пересчитанной на вход тракта при достижении заданного граничного уровня U гр, например 1мкВ, т. е.
D=20lg(U 1,i/ U гр) при U (2f2-f1)(N)= U грK1K2....KN. (2.5.9)
На рис. 2.5.4 показаны зависимости амплитуд основных и интермодуляционных колебаний третьего порядка при бигармоническом равноуровневом входном воздействии от числа идентичных усилительных каскадов
в тракте для частного случая К = 2 и D u = 1. Из рисунка видно, что, как для основных колебаний, так и для интермодуляционных, существуют хорошо выраженные зоны насыщения, которые характеризуются малой крутизной амплитудных характеристик.
| N=1 |
| N=2 |
| N=3 |
| N=4 |
| N=5 |
| N=6 |
| U 2,1-2 U 1,2 |
| 1.0 |
| 0.5 |
| 0.5 |
| 1.0 |
| 1.5 |
| U 1,2 ∆ u |
Рис. 2.5.3. Зависимость отношения амплитуды интермодуляционной составляющей 3-го порядка к спектральной составляющей меньшего уровня от числа усилительных каскадов в тракте при бигармоническом входном воздействии
|
|
|


