 |
№36 Метод таблиць істинності. №37 Умовивід: структура та види. №38 Безпосередній умовивід та його види. №39 Обґрунтування правил висновку
|
|
|
|
№36 Метод таблиць істинності
У логіці висловлювань процедури визначення кожної логічної операції задаються так званими таблицями істинності. Щоб побудувати таблицю істинності ми повинні прийняти такі умови:
1) просте висловлювання може бути або істинним, або хибним, але не можуть бути одночасно і істинним, і хибним; 2) кількість рядків таблиці істинності для певного складного висловлювання відповідає формулі: 2n (де 2 — кількість логічних значень для простого висловлювання
(істина та хиба), а n — кількість простих висловлювань, що входять до складу складного висловлювання). У логіці логічне значення «істина» позначається буквою «і», а логічне значення «хиба» — буквою «f». Наприклад, якщо до складу складного висловлювання входить два простих висловлювання, то відповідно до формули 2n замість п підставляємо 2 і отримуємо формулу 22 = 4.
№37 Умовивід: структура та види
Умовиводом називається така форма мислення або логічна операція, за допомогою якої із одного або декількох відомих суджень виводиться нове судження. Умовивід складається із: — засновків та — висновку. Засновками називаються раніше відомі судження, на підставі яких робиться висновок.
Висновком називається нове судження, отримане в результаті співставлення засновків. Наприклад,
1. Будь-який мешканець нашого будинку знає англійську мову. 2. Мій приятель мешкає в нашому будинку. 3. Отже, мій приятель знає англійську мову. 1 і 2 судження будуть засновками у а 3 судження — висновком. Всю множину умовиводів за характером зв'язку між засновками та висновком поділяють на: — дедуктивні; — індуктивні. У дедуктивному умовиводі ми переходимо від загального до часткового, або одиничного; в індуктивному —від одиничного до загального.
|
|
|
За ступенем обґрунтованості висновку умовиводи поділяють на: — демонстративні; — правдоподібні (імовірні). У демонстративних умовиводах висновок необхідно істинний, а в правдоподібних — імовірно істинний. За кількістю засновків умовиводи поділяються на — безпосередні; — опосередковані. Безпосереднім умовиводом називається такий умовивід, в якому висновок отримують із одного засновку. Опосередкованим умовиводом називається такий умовивід, в якому висновок отримують із двох і більше засновків. В залежності від того, чи випливає висновок із засновків з урахуванням логічної структури засновків, чи ні, умовиводи поділяються на силогізми та умовиводи логіки суджень або висновки логіки висловлювань.
№38 Безпосередній умовивід та його види
Безпосереднім умовиводом називається дедуктивний умовивід, у якому висновок отримують із
одного засновку. Види безпосередніх умовиводів на прикладах: Всі студенти історичного факультету вивчають логіку — (засновок): 1. Отже, деякі особи, що вивчають логіку є студентами історичного факультету — (висновок, отриманий шляхом обернення засновку ). 2. Жоден студент історичного факультету не може бути серед тих, хто не вивчає логіку — (отриманий шляхом перетворення засновку ). 3. Жоден, хто не вивчає логіку не належить до студентів історичного факультету — (отриманий, шляхом протиставлення предиката засновку до суб'єкта ). 4. Невірно, що деякі студенти історичного факультету не вивчають логіку (висновок, отриманий за правилом умовиводу по «логічному квадрату» ). Оберненням називається такий безпосередній умовивід у висновку якого суб'єктом стає предикат засновку, а предикатом — суб'єкт засновку. Схема цього умовиводу така: S є Р / Р є S. В умовиводі шляхом перетворення ми отримуємо висновок, де суб'єктом є суб'єкт засновку, а предикатом є поняття, що суперечить предикату засновку. Це стає можливим завдяки зміні якості засновку. Схемою такого умовиводу є: S є Р / S не є не – Р. Протиставленням предикату називається такий безпосередній умовивід у результаті якого отримують висновок суб'єктом якого є поняття, що суперечить предикату засновку, а предикатом стає суб'єкт засновку. Схема цього умовиводу така: S є Р / не - Р є S. Умовиводи, які будуються із урахуванням підпорядкування, суперечності, противності і підпротивності між категоричними судженнями, називають умовиводами за «логічним квадратом».
|
|
|
№39 Обґрунтування правил висновку
З точки зору синтаксису умовивід являє собою правило висновку. Правилом висновку є норма, що дозволяє із суджень однієї логічної структури як засновків отримувати судження певної логічної структури як висновок. Кожне правило репрезентує нескінченну множину умовиводів різноманітних за змістом, але єдиної синтаксичної структури. Правила висновку логіки висловлювань поділяються на: — основні та — похідні. Основними називаються правила, які змістовно очевидні і дозволяють відрізнити правильно побудовані міркування від неправильно побудованих міркувань.
Похідними називаються правила, які виводяться із основних і сприяють скороченню процесу
висновку. Розглянемо основні прямі правила: Правило введення кон'юнкції ( ВК ): 
. Прикладом змістовного міркування, що відповідає цьому правилу буде: Франція — європейська держава. Іспанія — європейська держава. Отже, Франція та Іспанія — європейські держави. Правило усунення кон'юнкції ( УК ): 
, 
. Приклад міркування, що відповідає правилу усунення кон'юнкції:
І. Теорія та гіпотеза — форми наукового пізнання. Отже, теорія — форма наукового пізнання.
II. Теорія та гіпотеза — форми наукового пізнання. Отже, гіпотеза — форма наукового пізнання. Правило введення диз'юнкції (ВД ): 
, 
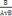. Приклад міркування, що відповідає правилу введення
диз'юнкції: Дана форма мислення є поняттям. Дана форма мислення є поняття або судження.
Правила усунення диз'юнкції (УД ): 
. Приклад міркування за правилом усунення диз'юнкції:
|
|
|
Він знає мого брата або мою сестру. Він не знає мою сестру. Отже, він знає мого брата. Правило усунення імплікації (УІ ): 
. Приклад міркування за правилом усунення імплікації: Якщо поїзд запізнюється, то ми не встигаємо на автобус. Поїзд запізнюється. Отже, ми не встигаємо на автобус. Правило введення еквіваленції (ВБ ): 
. Приклад міркування за правилом введення еквіваленції: Якщо на планеті є життя, тоді там є атмосфера. Якщо на планеті є атмосфера, тоді там є життя. Отже, на планеті є життя тоді і тільки тоді, коли там є атмосфера. Правило усунення еквіваленції (УЕ ): 
, 
. Правило введення подвійного заперечення (ВПЗ ): 
. Приклад міркування за правилом введення подвійного заперечення: Ця книжка є підручником з логіки. Отже, невірно, що ця книжка не підручник з логіки. Правило усунення подвійного заперечення (УПЗ ): 
. Приклад міркування за правилом усунення подвійного заперечення: Невірно, що курсова робота не виконана самостійно. Отже, курсова робота виконана самостійно. Розглянемо основні непрямі правила: Правило введення імплікації (ВІ ):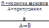 
. Правило введення заперечення (ВЗ ): «Якщо із засновків і довільного припущення А випливають два суперечливих висловлювання В і В, то таке припущення повинно бути визнаним як хибне, істинним визнається А ». Зупинимося на розгляді похідних правил висновку логіки висловлювань. Правило транзитивності імплікації (ТІ ): 
. Приклад міркування за правилом транзитивності імплікації: Якщо мовний відрізок розповідне речення, то він є висловлюванням. Якщо мовний відрізок є висловлюванням, то він є
осмисленим Отже, якщо мовний відрізок розповідне речення, то він є осмисленим. Правило заперечення диз'юнкції (ЗД ): 
. Відповідно до цього правила із заперечення диз'юнкції слідує кон'юнкція заперечень висловлювань, що її складають. Наприклад, Невірно, що він студент або школяр. Отже, він і не студент, і не школяр. Правило заперечення кон'юнкції (ЗК ): 
. Читається правило так: «Із заперечення кон'юнкції слідує диз'юнкція заперечень висловлювань, що складають
кон'юнкцію». Наприклад, Невірно, що дане космічне тіло має ознаки планети і природного супутника. Отже, дане космічне тіло, або немає ознак планети, або не має ознак природного супутника. Правило «modus tollens », або «від заперечення консеквентну до заперечення антецеденту» ( МТ ): 
. Наведемо приклад конкретного міркування, що регламентується цим правилом: Якщо він знає англійську мову, то він перекладе цей текст. Він не переклав цей текст.
|
|
|
Отже, він не знає англійської мови. Правило простої контрапозиції (ПК ): І. 
ІІ. 
. Наведемо приклад міркування, побудованого за правилом простої контрапозиції: Якщо лист написаний мною, то його зміст повинен бути мені відомим. Отже, якщо мені невідомий зміст листа, то він написаний не мною. Правило складної контрапозиції (ПСК ): І. 
; ІІ. 
. Наведемо приклад конкретного міркування за правилом складної контрапозиції: Якщо іспит з історії є першимі і він профілюючий, то, він є вирішальним для абітурієнта-медаліста. Отже, якщо іспит з історії є першим, але він не вирішальний для абітурієнта-медаліста, то він не профілюючий. Правило імпортації (ПІмп):
. Наведемо приклад міркування за цим правилом: Якщо він добре знає англійську мову, то у випадку, якщо приїде англійська делегація він зможе виконати роль перекладача. Отже, якщо він добре знає англійську мову і приїде англійська делегація, то він зможе виконати роль перекладача.
Правило експоратції (ПЕкс): 
. Наведемо приклад міркування за цим правилом: Якщо дана стаття ґрунтовна за змістом і відповідає тематиці збірника, то її слід публікувати. Отже, якщо дана стаття ґрунтовна за змістом, то у випадку, що вона відповідає тематиці збірника її слід публікувати.
На рівні семантики це можна зробити шляхом побудови таблиць істинності, шляхом еквівалентиних перетворень, методом аналітичних таблиць. На рівні синтаксису така перевірка здійснюється через побудову доведення останнього рядка правила. Розглянемо на прикладі правила транзитивності
імплікації його семантичне та синтаксичне обґрунтування (на предмет коректності). Спочатку зупинимося на семантичному обґрунтуванні. Побудова таблиць істинності, еквівалентні перетворення (КНФ) досить громіздкі, тому можна запропонувати такий спосіб. Відомо, що у правильному висновку між засновками і висновком існує відношення логічного слідування, тобто
при істинності засновків висновок повинен бути обов'язково істинним. Виходячи з цього в правилі ТІ між (А з В), (В з С) і (А з С) існує відношення логічного слідування, отже, засновки (А з В) і (В з С) не можуть бути істинними, а висновок (А з С) — хибним. Припустимо, що це не так (тобто, що А з В і В з С — істинні, а А з С — хибне). Тоді, А з С — хибне при умові А — і, С — х. А у засновках: якщо А — і, а С — х, то при будь-якому значенні В кон'юнкція засновків не буде істинною, а це суперечить нашому припущенню. Синтаксичне обґрунтування правила висновку передбачає побудову виведення останнього рядка із засновків. Для цього розгорнемо правило, вставивши між засновками і висновком проміжні ланки, які в правилі опущені. Доведення здійснюється таким способом: 1. Виписуємо засновки, що входять до правила. 2. Зліва виписуємо кроки доведення. 3. Справа напроти кожного кроку виписуємо його підставу (це може бути домовленість про введення
|
|
|
чергового припущення, або певне правило). Праву сторону такого запису називають аналізом доведення. Здійснимо доведення правила ТІ:
|
|
|
