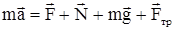|
Механика поступательного движения
|
|
|
|
Сборник задач по общей физике
для студентов ФАФО
Москва 2006
Задание 1 написано доц. Савельевой З. И. и Спиридоновой Л. В.; задание 2-ст. пр. Крикуновой Г. И.; задание 3-ст. пр. Герасимовой Э. О.; задание 4-доц. Грибковой Г. Н.; задание 5-доц. Гусевым А. Н. и доц. Ломакиной Е. В.; задание 6-доц. Богатыревым Ю. А. и доц. Родиной Т. В.; задание 7-ст. пр. Собоелвой Н. А. и доц. Соковишиным В. В.; задание 8-доц. Ивановым В. В.
Рецензенты:
Проф., д. т. н. Леончик Б. И., каф. «Теплотехника», МГУПП
доц., к. т. н. Зотов В. Е., каф. «Прикладная математика», МАИ (ГТУ)
Введение
Физика, как основа большинства современных естественных наук, позволяет описать объективные свойства окружающего нас материального мира. Изучая наиболее общие формы движения материи, она имела и имеет первостепенное значение при формировании концепций современного естествознания и является одним из важнейших компонентов подготовки современного инженера.
Настоящее пособие составлено коллективом преподавателей кафедры «физика» МГУПП в соответствии с существующей программой подготовки студентов инженерных специальностей. Оно построено таким образом, что может быть использовано для индивидуальной и самостоятельной работы студентов всех специальностей дневной и альтернативной форм обучения, а также для студентов очно-заочных групп.
Сборник состоит из восьми заданий в каждое из которых входят таблица вариантов, примеры решения задач и набор задач для самостоятельной работы.
Количество и объем индивидуальных заданий рассчитан на изучение физики в течении от одного до трех семестров. При этом в зависимости от запланированного на индивидуальную работу числа часов для студентов конкретной специальности ведущий преподаватель задает студентам своего потока номера вариантов каждого задания полностью или уменьшает число задач, комбинируя задания(например: вариант 1-задачи № 1, № 2 из первого задания и № 1, № 4 из второго задания и т. п. )Это позволяет гибко использовать материал сборника, в том числе и увеличивая число вариантов.
|
|
|
Общие указания
При выполнении каждого задания необходимо:
1. Записать полностью условие задачи.
2. Записать условие данной задачи аналитически, если это возможно.
3. Представить графическую иллюстрацию задачи, если это возможно
4. Составить систему уравнений, описывающих физические процессы, протекающие в ситуации, описанной в задаче. Число таких уравнений должно быть не менее, чем число тел задачи (материальных точек) умноженных на число координат в используемой системе отсчета.
5. Ззадачи желательно решать до конца в общем виде, за исключением особо громоздких. Числовые значения заданных величин подставлять только в окончательное рассчетное аналитическое выражение.
6. Форма представления ответов к задачам (единицы измерения, кратные и дольные приставки, округление)-произвольна. Исключения составляют ответы к задачам № 5, 6, 7 –их необходимо дать в системе СИ.
ЗАДАНИЕ №1
Механика поступательного движения
Таблица вариантов
| Номера вариантов | Номера задач по порядку | ||||
| 89* | |||||
|
|
|
Примеры решения задач
Пример №1. Уравнение движения материальной точки имеет вид:
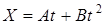 , где А = 2 м/с, В = - 0, 2 м/с. Определить средние значения скорости и ускорения в интервале времени от 2-х до 4-х секунд.
, где А = 2 м/с, В = - 0, 2 м/с. Определить средние значения скорости и ускорения в интервале времени от 2-х до 4-х секунд.
Прежде всего запишем условие задачи в аналитическом виде:
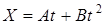 А = 2 м/с
В = - 0, 2 м/с
А = 2 м/с
В = - 0, 2 м/с
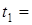 2 с 2 с
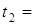 4 с 4 с
| 
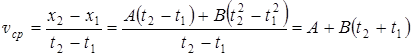 υ ср = 0, 8 м/с
υ ср = 0, 8 м/с
|
| υ ср -? aср -? | По определению среднего ускорения, оно равно |
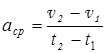
Мгновенная скорость может быть получена из уравнения
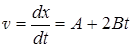
Подставив это выражение в уравнение для среднего ускорения, получим
 ,
,
т. е. ускорение точки при заданном законе движения постоянно, что с очевидностью получается из уравнения движения, поскольку ускорение может быть получено двойным дифференцированием по времени координаты точки:

Пример №2 . С какой высоты упало тело, если вторую половину пути оно пролетело за 1 с?
Проиллюстрируем задачу графически, что позволит записать правильно в аналитической форме ее условия
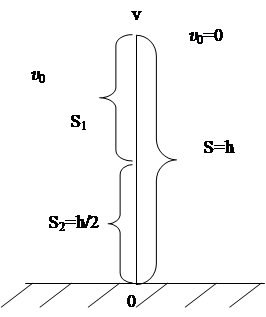
 0 = 0
S = h
S2 = h/2 0 = 0
S = h
S2 = h/2
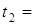 1 с 1 с
| Однако, поскольку на нижнем отрезке S2 пути движение происходило с неизвестной нам начальной скоростью, рационально записать уравнение движения для всего отрезка и верхнего участка S1, поскольку в этих случаях начальная скорость равна нулю. Учтем, что S1=S-S2 = h/2 и |
| h -? |
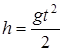
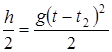
Подставляя верхнее уравнение в нижнее уравнение, получим
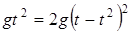 ;
; 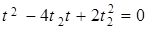
Решение этого уравнения имеет вид
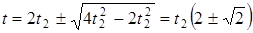
t =3, 41 с; t =0, 59 с
Второе решение квадратного уравнения не подходит по смыслу – все время движения не может быть меньше времени движения на втором участке пути. Подставляя в выражение для h значение t, получаем
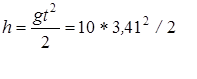
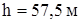
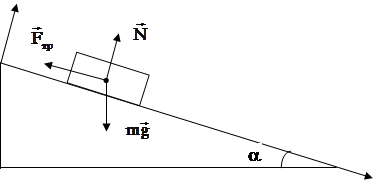
Пример №3. Человек тянет груз за верёвку, при этом верёвка составляет с горизонталью угол 45°, а коэффициент трения груза с горизонтальной поверхностью составляет 0, 01. Определите ускорение груза, если его масса 40 кг, а сила, приложенная человеком к верёвке, 50Н.
(Принять sin45° = cos45° = 0, 7)
|
|
|
|
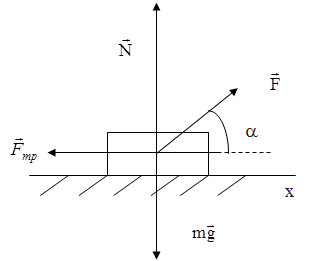 |
| F = 50 H m = 0, 01 m = 40 кг g = 10 м/с a = 45° | Составим систему уравнений, описывающих движение тела. Основное уравнение движения в векторной форме будет иметь вид:
Для решения задачи его надо написать в скалярной форме т. е. в проекциях на оси ОХ и ОУ: |
| a -? |
 ,
, 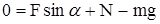 ,
,
кроме того, нужно учесть зависимость силы трения от силы реакции опоры N:
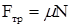 ,
,
Решая совместно полученные уравнения, получим
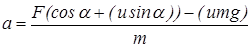
После подставления численных значений получим а = 0, 78м/с2.
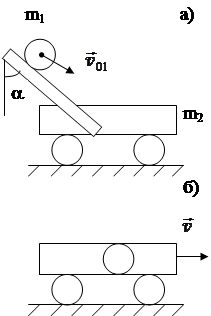 Пример №4. Шарик массой 20 г скатывается по жёлобу, наклонённому под углом 60° к вертикали, на неподвижную тележку массой 2кг. Какую скорость приобретёт тележка, если удар о неё шарика можно считать абсолютно неупругим?
Пример №4. Шарик массой 20 г скатывается по жёлобу, наклонённому под углом 60° к вертикали, на неподвижную тележку массой 2кг. Какую скорость приобретёт тележка, если удар о неё шарика можно считать абсолютно неупругим?
 Изобразим на рисунке а) положение тележки и шарика непосредственно перед ударом; на рисунке б) нарисуем векторы скоростей тел после удара и, поскольку перед ударом скорость шарика была направлена под углом к горизонтали, разложим её на составляющие. Примем при этом за положительное направление оси ОХ направление по горизонтали в сторону направления горизонтальной составляющей скорости движения шарика, а за положительное направление оси ОУ- направление по вертикали вниз.
Изобразим на рисунке а) положение тележки и шарика непосредственно перед ударом; на рисунке б) нарисуем векторы скоростей тел после удара и, поскольку перед ударом скорость шарика была направлена под углом к горизонтали, разложим её на составляющие. Примем при этом за положительное направление оси ОХ направление по горизонтали в сторону направления горизонтальной составляющей скорости движения шарика, а за положительное направление оси ОУ- направление по вертикали вниз.
Затем запишем в аналитической форме условие задачи
| υ 0 = 0 υ 01= 2 м/с m1 = 0, 02 кг m2 = 2 кг a = 60° | Очевидно, что в рассматриваемом случае выполняется закон сохранения импульса для системы шарик-тележка, но только в проекции на ось ОХ, так как в вертикальном направлении импульс шарика при ударе о пол тележки полностью гасится. |
| υ -? |
Запишем значения импульсов системы до и после удара: импульс системы перед ударом:
|
|
|
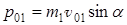
После удара: p = (m1+m2) 
Теперь запишем закон сохранения импульса вдоль оси ОХ: 
или 
Решив это уравнение, мы найдем скорость тележки после удара:
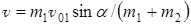
После подстановки числовых значений получим
υ = 0, 02 м/с
Пример №5. Какую скорость приобретает тело, скользящее с наклонной плоскости, пройдя по ней путь 10 м, если коэффициент трения скольжения его о поверхность плоскости 0, 1, а угол наклона плоскости к горизонту 30 °?
Сделаем рисунок, иллюстрирующий условие задачи, выбрав за ось ОХ направление по плоскости вниз (в сторону движения тела). Разложим силу тяжести на составляющие, поскольку её направление не совпадает с направлением осей координат. Затем запишем условие задачи в аналитической форме.
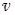 0 = 0
L = 10 м
m = 0, 1
a = 30° 0 = 0
L = 10 м
m = 0, 1
a = 30°
|
| ||||||||||||||||||||||||||||||||||
| υ -? | |||||||||||||||||||||||||||||||||||
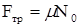
Ни один из законов сохранения механики не выполняется, а применение законов Ньютона делает решение довольно громоздким. Поскольку в задаче действует диссипативная сила - сила трения, то часть первоначальной потенциальной энергии тела, которую оно имело в начале движения, переходит в тепловую за счёт совершения работы по преодолению силы трения. Тогда закон сохранения полной энергии может быть применен в виде:
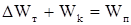 ;
; 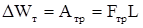
Считая систему плоскость-тело изолированной, величину силы трения найдём из условия равновесия сил по оси У:
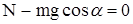 ;
; 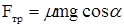
Подставив это выражение в уравнение закона сохранения энергии, получим:
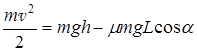 ;
; 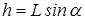
Откуда и получим выражение для скорости:
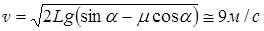
|
|
|



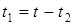 , тогда получим следующую систему
, тогда получим следующую систему