Главная | Обратная связь | Поможем написать вашу работу!

Механика вращательного движения

Механика вращательного движения

Таблица вариантов

Номера вариантов	Номера задач по порядку
	1		37	58	40
	4		39	59	37
	2		38	55	43
	3			57
			42	56
	5		40		44
	6		44
	12	28	48		49
	13	35	43
	16	32	41	60	55
		33	45	59
	7		50	60	58
	8		47	13	40
	17		48	45	56
			52	60
	11		49	58	53
	13		51	42	59
	14	36	53	51	48
	1		50		45
	9		45		40
	11	36		50	43
	5		43	59	58
	12		44
	2		42	60
		28	48	36	41
	13		47	45	37
	16	35	51	58	38
	14	32	41		49
	15		39	60	52
	17		38	56	47

Примеры решения задач

Пример №1. Маховик, двигаясь равноускоренно, за 20с увеличил частоту вращения от 2об/с до 7об/с. Сколько оборотов сделал он за это время?

Решение. При равноускоренном движении угловое перемещение определяется из соотношения:

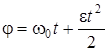
По определению 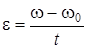, следовательно

Угловое перемещение связано с числом оборотов соотношением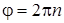

Угловые скорости выражаем через начальную и конечную частоту:

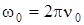, , теперь получим выражение для нахождения числа оборотов:

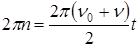Откуда получим

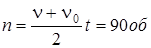
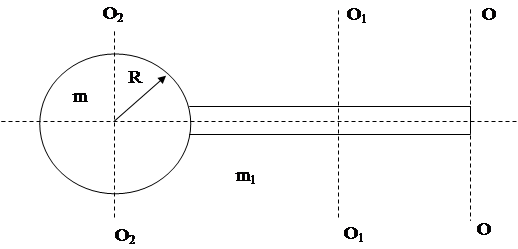
Пример №2. К шару массой 2кг и радиусом 10см прикреплен стержень массой 4, 8 кг и длиной 1, 2 м и является продолжением диаметра шара. Найти момент инерции системы относительно оси, проходящей через

свободный конец стержня перпендикулярно к нему.

Решение. Момент инерции шара относительно оси О₂О₂

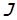
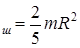
Момент инерции шара относительно оси ОО по теореме Штейнера

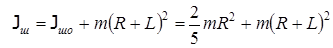
Момент инерции стержня относительно оси О₁О₁

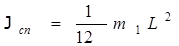
Момент инерции стержня относительно оси ОО по теореме Штейнера:

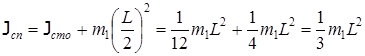
Суммарный момент инерции относительно оси ОО:

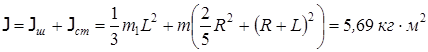
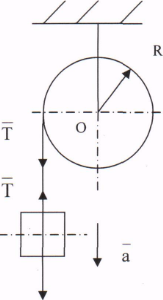
Пример №3. Блок имеет неподвижную ось вращения. Масса блока 1кг, радиус 0, 2 м. На блок намотана нить, к концу которой привязан груз массой 2 кг. С каким ускорением будет опускаться груз?

Решение. Груз движется поступательно, 2-ой закон Ньютона для него имеет вид: 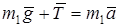. В проекции на ось у получим

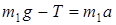(1).

Блок вращается равноускоренно, для него запишем основное уравнение динамики вращательного движения:

М = 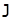e (2)

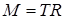где (3)

Для однородного диска 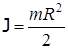(4)

Угловое ускорение связано с тангенциальным ускорением следующим соотношением

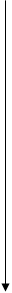
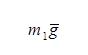
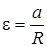(5)

Подставив выражения (3), (4), (5) в уравнение (2), получим

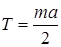(6)

Решая совместно (1) и (6), получим

;

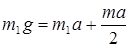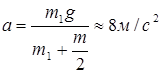
Пример №4. Человек массой 60кг стоит на краю платформы, имеющей форму диска радиусом 1м. Момент инерции платформы 20 кг·м². Платформа вместе с человеком вращается с угловой скоростью 1 рад/с. Какую работу совершит человек если перейдёт в центр диска. Момент инерции человека считать как для материальной точки.

Решение. Поскольку взаимодействие происходит только между человеком и платформой, систему считаем замкнутой и применяем закон сохранения момента импульса. В начальный момент времени момент инерции системы:

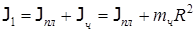
а момент импульса системы:.

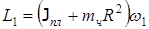
Когда человек перешел в центр платформы, его момент инерции стал равен нулю, угловая скорость изменилась до w₂, а момент импульса: L₁=L₂

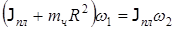
откуда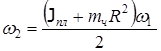

Начальная кинетическая энергия системы

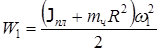
Человек, перейдя в центр диска, совершил работу, что привело к изменению кинетической энергии системы до

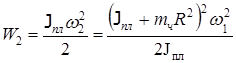по закону сохранения энергии работа:

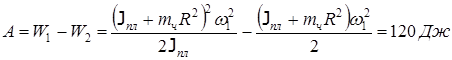
(При решении задачи принять g = 9, 8 м/с²)

Задачи для самостоятельного решения

1. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 об после начала движения. Найти угловое ускорение колеса.

2. Маховик, спустя 1 минуту после начала вращения приобретает скорость, соответствующую частоте 20 об/с. Считая движение равноускоренным, найти угловое ускорение и число оборотов колеса за эту минуту.

3. Колесо, вращаясь равно замедленно, при торможении уменьшило за 1 минуту частоту вращения с 300 об/мин до 180 об/мин. Найти угловое ускорение колеса и число оборотов за это время.

4. Вентилятор делает 900 оборотов в минуту. После выключения он вращается равно замедленно, сделав до остановки 75 оборотов. Сколько времени прошло с момента выключения до полной остановки вентилятора?

5. Вал вращается с постоянной скоростью, соответствующей частоте 180 об/мин. С некоторого момента вал тормозится и вращается равно замедленно с угловым ускорением, численно равным 3 рад/с². Через сколько времени вал остановится и сколько оборотов сделает за это время?

6. Точка, равномерно вращаясь, делала 100 оборотов в минуту. Начав тормозить, она остановилась через 30 с. Сколько оборотов она сделала до остановки?

7. Диск равномерно вращается. Под действием тормозящего момента он начинает двигаться равно замедленно и останавливается через 10 с, сделав 50 оборотов. Каков был период вращения диска до торможения?

8. Точка движется по окружности радиусом 1 м с постоянным тангенциальным ускорением 1 см/с². Через сколько времени нормальное ускорение будет равно тангенциальному?

9. Точка, двигаясь по окружности радиусом 0, 1 м равноускоренно, достигает к концу 10-го оборота линейной скорости 3, 14 м/с. Найти тангенциальное ускорение.

10. Колесо радиусом 20 см вращается равноускоренно с угловым ускорением 0, 157 рад/с². Найти нормальное ускорение точек его поверхности через 5 с после начала вращения.

11. Колесо вращается равноускоренно с угловым ускорением 0, 43 рад/с². Найти угол между вектором скорости и вектором ускорения /полного/ точки на ободе через 2 с.

12. Точка движется по окружности радиусом 2 см. Зависимость пути от времени дается уравнением S=Сt³, где С= 0, 1 см/с^З. Найти тангенциальное и нормальное ускорения точки в тот момент, когда скорость точки равна 0, 3 м/с.

13. Колесо вращается так, что зависимость угла поворота от t дается

уравнением

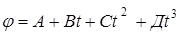
где В = 1 рад/с, С = 1 рад/с², Д = 1 рад/с³. К концу второй секунды нормальное ускорение точек на ободе колеса равно 346 м/с². Найти радиус колеса.

14. Точка движется по окружности радиуса 0, 2 м. равноускоренно с

угловым ускорением 0, 1 рад/с². Через сколько времени угол между полным ускорением точки и ее скоростью будет равен 45°? Начальная скорость равна 0.

15. Точка движется по окружности радиусом 0, 2 м так, что путь определяется по закону: S= Аt+Вt³, где А=2 м/с, В= - 0, 1 м/с³. Найти тангенциальное и нормальное ускорение через 2с.

16. Точка движется по окружности так, что путь определяется

уравнением: S= А+Вt², где В = 0, 1 м/с². Через 1, 6 с после начала движения тангенциальное ускорение стало равно нормальному. Найти радиус окружности.

17. Точка движется по окружности радиусом 0, 125 м с тангенциальным ускорением 0, 5 м/с² без начальной скорости. Через сколько времени полное ускорение будет равно 0, 7 м/с²?

18. Четыре маленьких шарика массой 50 г каждый помещены в вершинах квад-рата со стороной 20 см. Найти момент инерции системы относительно оси, проходящей через центр квадрата перпендикулярно его плоскости.

Шарики скреплены невесомыми стержнями.

19. Два шара массой 1 кг и радиусом 10 см каждый соединены стержнем с массой 2 кг и длиной 60 см. Найти момент инерции системы относительно оси, проходящей через середину стержня перпендикулярно к нему.

20. Решить предыдущую задачу относительно оси, отстоящей от середины стержня на 20 см.

21. Решить задачу 19 относительно оси, проходящей перпендикулярно стержню на расстоянии 30 см от его середины.

22. Найти момент инерции шара относительно оси, проходящей парал-лельно его диаметру на расстоянии половины радиуса от него. Масса шара 2 кг, радиус 20 см.

23. Решить предыдущую задачу для оси, касающейся поверхности шара.

24. Рассчитать момент инерции полого тонкостенного цилиндра массой 4 кг, радиусом 40 см относительно оси, совпадающей с образующей цилиндра.

25. Найти момент инерции диска относительно оси, проходящей перпендикулярно его плоскости на расстоянии 1/3 его радиуса от центра диска. Масса диска 2 кг, радиус = 30 см.

26. Поверхности двух шаров радиусами 10 см и 20 см соприкасаются в точке А. Массы шаров соответственно 2 кг и 4 кг. Найти момент инерции системы относительно оси, проходящей через точку А перпендикулярно отрезку, соединяющему центры шаров.

27. Поверхности двух шаров одинакового радиусе 20 см соприкасаются. Массы шаров 1 кг и 2 кг. Найти момент инерции системы относительно оси, проходящей через точку соединения шаров перпендикулярно отрезку, соединяющему их центры.

28. Поверхности двух шаров одинаковой массы 2 кг, но разных радиусов, соприкасаются. Момент инерции системы относительно оси, проходящей через точку соприкосновения шаров перпендикулярно отрезку, соединяющему их центры, равен 0, 091 кг× м². Найти радиус первого шара, если радиус второго = 10 см.

29. Три одинаковых маленьких шарика массой 100 г каждый помещены в вершинах правильного треугольника со стороной 10 см. Найти момент инерции системы относительно оси, проходящей перпендикулярно плоскости треугольника через его центр.

30. К шару радиусом 10 см и массой 2 кг присоединен стержень длиной 40 см и массой 6 кг. Ось стержня проходит через центр шара. Найти момент инерции системы относительно оси, проходящей через точку соединения шара и стержня перпендикулярно к стержню.

31. Решить предыдущую задачу относительно оси, проходящей через центр стержня перпендикулярно к нему.

32. К ободу однородного диска радиусом 0, 2 м приложена касательная сила 100 Н, а момент сил трения = 5 Нм. Найти угловое ускорение диска, если его масса = 10 кг.

33. К ободу диска радиусом 20 см с моментом инерции 2 кг·м² приложена касательная сила 50 Н. Какова будет угловая скорость через 10 с после начала действия этой силы, если момент сил трения 8 Нм?

34. Под действием касательной силы однородный диск радиусом 20 см и массой 4 кг вращается ускоренно с угловым ускорением 0, 2 рад/с². Каков должен быть момент силы торможения, чтобы он стал вращаться равномерно?

35. Однородный стержень длиной 1 м вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через его середину, с угловым ускорением 2, 35 рад/с². Какова масса стержня, если вращающий момент 0, 47 Нм?

36. Однородный стержень вращается в вертикальной плоскости вокруг оси, проходящей на расстоянии 1/3 длины стержня от его конца. Длина стержня 60 см, масса 3 кг. Вращающий момент 2, 4 Нм. С каким угловым ускорением вращается стержень?

37. Однородный диск радиусом 0, 2 м и массой 5 кг вращается вокруг оси, проходящей через его центр. Угловая скорость его изменяется по закону: w= А + Вt, где В = 8 рад/с². Найти величину касательной силы, приложенный к ободу диска.

38. Однородный диск радиусом 40 см, массой 10 кг вращается равноускоренно под действием касательной силы Р так, что за 10 с угловая скорость увеличилась от 6 рад/с до 36 рад/с. Найти силу Р.

39. Маховик с моментом инерции 63, 6 кг·м² вращается с угловой скоростью 31, 4 рад/с. Через сколько секунд он остановится, если на него действует тормозящий момент 100 Н·м?

40. Полый цилиндр радиусом 0, 4 м вращается с угловой скоростью 2 рад/с. Когда на него подействовала касательная сила 24 Н, за 3 с угловая скорость увеличилась до 20 рад/с. Найти массу цилиндра.

41. Маховик, имеющий момент инерции 245 кг·м², вращается с частотой 20 об/с. Под действием сил трения он остановился, сделав 600 оборотов. Найти момент сил трения.

42. Шар радиусом 20 см равномерно вращается с частотой 10 об/с. Под действием момента сил трения 1, 8 Н·м он остановился, сделав 14 оборотов. Найти массу шара.

43. Две гири с массами 1 кг и 2 кг соединены нитью, перекинутой через блок, являющийся однородным диском с массой 1 кг. Найти ускорение, с которым движутся гири, и силы натяжения частей нити, к которым привязаны гири.

44. На сплошной цилиндр массой 9 кг намотан шнур, к концу которого привязан груз массой 2 кг. Найти ускорение груза. Трением пренебречь.

45. На полый тонкостенный цилиндр намотан шнур, к концу которого привязана гиря массой 5 кг. Гиря начала опускаться равноускоренно и за первые 2 с прошла 4 м. Найти массу цилиндра.

46. На барабан радиусом 0, 5 м намотан шнур, к концу которого привязана гиря массой 10 кг. Груз опускается с ускорением 2 м/с². Найти момент инерции барабана.

47. На полый тонкостенный цилиндр намотан шнур, к концу которого привязан груз массой 4, 5 кг, находящийся на высоте Н. Нить начинает раскручиваться, и груз достигает пола за 2 с. Масса цилиндра 10, 5 кг. Найти Н.

48. На полый тонкостенный цилиндр намотана невесомая нить, свободный конец которой прикреплен к кронштейну. С каким ускорением будет опускаться цилиндр под действием силы тяжести.

49. На сплошной цилиндр массой 9 кг намотан шнур, к концу которого привязан груз массой 2 кг. Найти ускорение груза. Трением пренебречь.

50. Два тела массами m₁ =1, 5 кг и m₂ = 2, 5 кг связаны тонкой нитью, переброшенной через блок. Блок укреплен на краю стола, по поверхности которого скользит тело m₂, а другое тело движется вниз. Коэффициент трения груза о поверхность стола 0, 2. Масса блока 1 кг и ее можно считать распределенной по ободу. Найти ускорение грузов и силы натяжения нити по обе стороны от блока.

51. Решить предыдущую задачу при условии, что массы грузов т₁=т₂= 2 кг, а блок - сплошной диск массой 0, 4 кг.

52. Человек стоит на скамье Жуковского на расстоянии 0, 8 м от оси вращения. С какой угловой скоростью начнет вращаться скамья Жуковского с человеком, если человек бросит мяч массой 0, 5 кг с горизонтальной скоростью 20 м/с в направлении, перпендикулярном к радиусу, соединяющему человека с осью скамьи. Момент инерции скамьи 5 кг·м², масса человека 60 кг. Момент инерции человека рассчитывать, как для материальной точки.

53. На краю круглой платформы массой 200 кг и радиусом 2 м стоит человек массой 60 кг. Когда человек пошел с постоянной скоростью вдоль края платформы, платформа начала вращаться с угловой скоростью 0, 3 рад/с. Найти скорость человека относительно платформы.

54. В предыдущей задаче найти, на какой угол повернется платформа, когда человек, обойдя ее вернется в исходную точку на платформе?

55. Платформа в виде диска радиусом 1 м вращается с частотой 2с^-1. В центре ее стоит человек массой 60 кг. С какой частотой начнет вращаться платформа, если человек перейдет на ее край? Момент инерции платформы 40 кг·м², момент инерции человека рассчитывать, как для материальной точки.

56. Платформа в виде диска радиусом 1м вращается с частотой 2 с^-1. Человек массой 60 кг стоит на расстоянии половины радиуса от центра платформы. С какой частотой начнет вращаться платформа, если человек перейдет на ее край? Момент инерции платформы 40 кг·м². Момент инерции человека рассчитывать, как для материальной точки.

57. В центре скамьи Жуковского стоит человек. В руках он держит посередине горизонтальный стержень длиной 2 м, массой 12 кг. Скамья вращается с частотой 1, 8 с^-1. С какой частотой будет вращаться скамья, если человек повернет стержень в вертикальное положение вдоль оси вращения? Суммарный момент инерции человека и скамьи 6 кг·. м².

58. Сплошной цилиндр массой 40 кг и радиусом 20 см покоится. Какую работу необходимо совершить, чтобы сообщить цилиндру частоту 5 с^-1.

59. Шар радиусом 20 см и массой 15 кг вращается, делая 120 оборотов в минуту. Какую работу должна совершить сила трения, чтобы остановить его?

60. Сплошной цилиндр массой 20 кг, радиусом 40 см вращается. Под действием сил трения он движется замедленно и останавливается, причем работа сил трения 1568 Дж. С каким периодом вращался цилиндр до начала торможения?

61. Вентилятор вращается равномерно, делая 900 оборотов в минуту. После выключения он останавливается под действием сил торможения. Работа сил торможения 44, 4 Дж. Найти момент инерции вентилятора.

62. Вентилятор вращается равномерно. После его выключения он останав-ливается, сделав до остановки 75 оборотов. Работа сил торможения 44, 4 Дж. Найти момент сил торможения.

ЗАДАНИЕ №3

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Воспользуйтесь поиском по сайту: