 |
Изучение крутильного маятника.
|
|
|
|
1.Цель работы.
Изучение колебательных процессов на примере крутильного маятника.
2. Основы теории.
Рассмотри крутильные колебания вокруг оси ОС диска посаженного на торсион (упругий стержень, работающий на кручение), второй конец которого жестко закреплен в корпусе (рисунок 1). При повороте диска на малый угол 
возникает момент восстанавливающей силы, который в области упругой деформации торсиона пропорционален углу поворота :
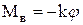, (1)
где k – коэффициент угловой жесткости упругого элемента, т.е. момент который создал бы упругий элемент с линейной характеристикой при =1 рад.
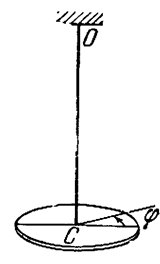
Рисунок 1. – К выводу уравнения крутильных колебаний.
Если пренебречь моментом инерции торсиона, то момент сил инерции крутильного маятника:
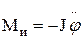, (2)
где J – момент инерции диска вокруг оси ОС динамической симметрии.
Момент демпфирования колебаний, обусловленный трением о воздух и вязким трением в материале торсиона равен:
,
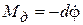где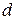 
- коэффициент демпфирования.
Методом Даламбера можно получить уравнения колебаний диска:
. (3)
Поделив на коэффициент при старшей производной получим:
. (4)
Перепишем последнее уравнение в виде:
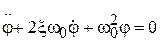, (5)
где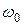 
- частота собственных незатухающих колебаний, 
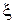- относительный коэффициент демпфирования:
, 
. (6)
Решение уравнения (6) имеет вид:
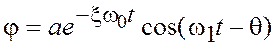, (7)
где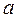 
– амплитуда колебаний;
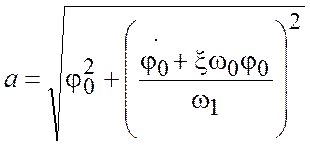; (8)
- начальный угол отклонения маятника от вертикали;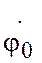 
- начальная скорость колебаний; 
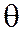- фаза колебаний;
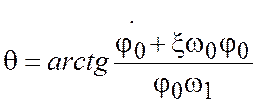. (9)
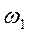- круговая частота затухающих колебаний;
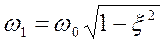. (10)
Из решения (10) видно, что при вязком трении колебания осциллятора будут затухать по экспоненциальному закону, как показано на рис.2).
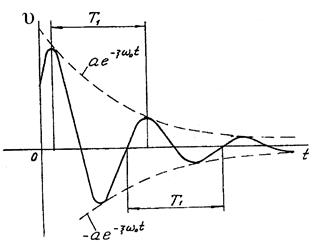
Рис.2. Колебания крутильного маятника
Скорость затухания колебаний маятника, зависящая от свойств торсиона, характеризуется показателем затухания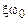 
. Показатель затухания – это величина обратная промежутку времени 
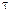, в течение которого амплитуда колебаний убывает в 
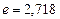раз. Отсюда:
|
|
|
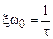. (11)
Графически время 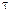, а, следовательно, и скорость затухания можно найти через построение касательных к огибающей колебания (рис. 3).
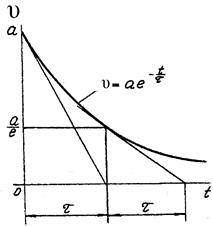
Рис. 3 - К определению вязкого трения в торсионе.
Сопоставив выражения (10) и (11) можно записать:
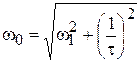. (12)
Следовательно:
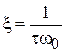(13)
Таким образом, можно определить внутренне трение в торсионе.
3. Объект исследования.
Объектом исследования является крутильный маятник (рисунок 4).
Рис. 4. Внешний вид лабораторной установки
4.Последовательность проведения работы.
1. Отклонит маятника на малый угол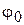 
=10 град и отпустить его. При качке маятника замерить:
а) период затухающих колебаний Т1;
б) число колебаний прошедших от начала качки до того момента пока амплитуда не уменьшится до 7, потом до 5, потом до 3, потом до 1 град.
2. По результатам измерений заполнить таблицу:
Амплитуда,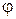 
| Число колебаний, n | Время колебаний, t= T1*n | |
| град. | рад. | - | сек. |
3. Построить график колебаний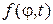 
.
4. Определить частоту собственных затухающих колебаний и (графическим методом) время .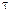
5. По формуле (12) определить частоту собственных незатухающих колебаний.
6. По формуле (13) определить относительный коэффициент демпфирования.
7. По формуле (6) определить коэффициент демпфирования.
8. В качестве торсиона установить пластину номер два и построить пункты 1 – 7.
5. Контрольные вопросы.
5.1 Поясните графический метод определения коэффициента затухания.
5.2 Каким образом наличие вязкого трения влияет на вид затухающих колебаний?
5.3 Составьте уравнение затухающих колебаний крутильного маятника.
|
|
|
6. Библиографический список.
6.1. Савельев В.В. Прикладная теория колебаний: Учебн. пособ. – Тула: ТулГУ. – Тула, 2005. – 160 с.
|
|
|
