 |
Расчет и экспериментальное определение частоты собственных колебаний упругого элемента
|
|
|
|
1.Цель работы.
Освоение методики теоретического расчета и экспериментального определения круговой частоты собственных колебаний упругого элемента.
2. Основы теории.
Рассмотрим плоскую пружину, один конец которой жестко закреплен, а на другом помещен груз массой 
(рис. 1). Под действием веса груза пружина деформируется - прогнется на величину 
.
Рис.1. К определению круговой частоты собственных незатухающих колебаний осциллятора
В случае равновесия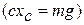 
жесткость пружины 
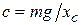. Из последнего равенства следует, что 
, а так как круговая частота собственных колебаний 
, то
. (1)
Таким образом, методика теоретического расчета частоты собственных незатухающих колебаний сводится к выполнению двух пунктов:
- измерить статический прогиб;
- рассчитать частоту.
Экспериментальное определение несколько сложнее, так как упругий элемент совершает колебания с частотой затухающих колебаний:
, (2)
где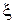 
- относительный коэффициент демпфирования.
Т.е. непосредственно опытным путем можно измерить не 
, а 
. Для того, что бы определить необходимо знать величину 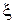. Её можно определить по графику затухающих колебаний.
Пусть имеется график колебаний (рис.2).
- амплитуда колебаний в момент времени 
, 
- амплитуда колебаний в момент времени 
, 
- период собственных затухающих колебаний
Рис. 3. К пояснению метода определения относительного коэффициента демпфирования
Известно, что
.
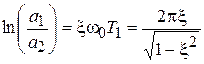Откуда можно найти:
. (3)
Таким образом, методика экспериментального определения частоты собственных незатухающих колебаний сводится к выполнению четырех пунктов:
- экспериментальное получение графика затухающих колебаний;
- определение по графику , и ;
|
|
|
- вычисление и вычисление по формуле (3) величины ;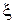
- вычисление по формуле (2) величины .
3. Объект исследования.
Объектом исследования является плоский упругий элемент, на конце которого закреплен пьезоэлектрический акселерометр ДН-4 (рисунок 3). В качестве плоского упругого элемента используется стальная пластина (линейка).
1 – плоский упругий элемент (стальная линейка), 2 – пьезоэлектрический акселерометр ДН-4, 3 – осциллограф, 4 – кабель передачи сигнала
Рис.3. Внешний вид лабораторной установки
Статический прогиб упругого элемента под действием массы ДН-4 измеряется с помощью второй линейки. Для определения периода затухающих колебаний, а также амплитуды колебаний применяется датчик ДН-4, который подключен к осциллографу.
4.Последовательность проведения работы.
4.1 Расчет круговой частоты собственных колебаний упругого элемента.
4.1.1. Закрепить датчик ДН-4 на конце упругого элемента.
4.1.2. Другой конец упругого элемента неподвижно закрепить на столе так, чтобы длина упругого элемента составляла 10см.
4.1.3. Измерить статический прогиб упругого элемента.
4.1.4. По формуле (1) рассчитать частоту собственных колебаний.
4.1.5. Повторить пункты 4.1.2 – 4.1.4 при длине упругого элемента 15см.
4.2 Экспериментальное определение круговой частоты собственных колебаний упругого элемента.
4.2.1. Закрепить датчик ДН-4 на конце упругого элемента.
4.2.2. Другой конец упругого элемента неподвижно закрепить на столе так, чтобы длина упругого элемента составляла 10см.
4.2.3. Подключить датчик ДН-4 к осциллографу.
4.2.4. Записать график затухающих колебаний. Данный график необходимо включить в отчет.
4.2.5. По графику определить величины (в секундах), и (в вольтах).
4.2.6. Вычислить и по формуле (3) вычислить .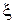
4.2.7. Вычислить по формуле (2) величину .
4.2.8. Повторить пункты 4.2.2. – 4.2.7 при длине упругого элемента 15см.
|
|
|
4.3. Заполнить таблицу.
| Длина упругого элемента | Теоретический расчет | Экспериментальное определение | |
|
|
|
| |
| 10см | |||
| 15см |
4.4. Сделать вывод по результатам проведенной работы.
5. Контрольные вопросы.
5.1. Выведите выражение (1).
5.2. выведите выражение (3).
5.3. Поясните причины разницы величины рассчитанной теоретически и полученной экспериментально.
6. Библиографический список.
6.1. Савельев В.В. Прикладная теория колебаний: Учебн. пособ. – Тула: ТулГУ. – Тула, 2005. – 160 с.
|
|
|
