 |
Изучение работы квазистатического прибора
|
|
|
|
1. Цель работы.
Изучить назначение, принцип работы сейсмических и квазистатических приборов, проанализировать работу приборов при различных частотах колебаний корпуса с помощью компьютера.
2. Основы теории.
Сейсмические приборы применяются для измерения перемещений: угловых и линейных колебаний подвижных объектов, уровня вибраций в различных точках внутри подвижных объектов (железнодорожные вагоны, автомобили, летательные аппараты). Сейсмическими эти приборы называются потому, что они построены по тому же принципу, что и сейсмограф – прибор для измерений колебаний почвы. Основой таких приборов является механическая колебательная система, которая с заданной точностью сохраняет неизменной положение по отношению к неподвижной системе координат. Эта механическая система моделирует неподвижную систему отчета, по отношению к которой определяется перемещение объекта (корпуса прибора).
Схема сейсмического прибора показана на рисунке 1.
Рис. 1 Схема сейсмического прибора
Перемещение инерциальной массы m относительно корпуса описывается уравнением:
, (1)
где 
– масса осциллятора; 
– коэффициент демпфирования; 
- коэффициент жесткости упругого элемента, 
- ускорение корпуса по отношению к неподвижной системе координат.
Если положить, что перемещение корпуса происходит по закону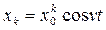 
, где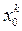 
- амплитуда, а 
- круговая частота колебаний корпуса, то частное решение уравнения (1), соответствующее вынужденным колебаниям инерциальной массы относительно корпуса прибора имеет вид:
, (2)
где 
- коэффициент динамичности; 
- сдвиг фазы вынужденных колебаний по отношению к колебаниям корпуса:
; (3)
|
|
|
, (4)
где 
- круговая частота собственных незатухающих колебаний, 
; 
- относительный коэффициент демпфирования, 
.
Рис. 2 Зависимость сдвига фазы от отношения круговых частот
Рис.3 Зависимость коэффициента динамичности от отношения круговых частот
Графики зависимости 
и 
от отношения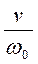 
для различных значений 
показан на рисунках 2 и 3.
Для того, что бы колебания 
точнее отображали колебания 
необходимо 
, а 
. Тогда
. (5)
Можно утверждать, что (5) идеальное уравнение сейсмического прибора (с точностью до знака). Относительная динамическая погрешность прибора может быть вычислена по формуле:
, (6)
а фазовая динамическая погрешность – по формуле
. (7)
По заданным значениям 
и 
формулы (6) и (7) можно вычислить требуемое соотношение частот 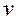и .
В случае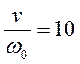 
, 
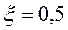, воспользовавшись формулами (6) и (7), получим 
и 
.
Таким образом, если круговая частота 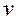колебаний объекта (корпуса) значительно больше круговой частоты собственных колебаний измерительного прибора, то колебания с точностью до знака повторяют колебания корпуса. Для получения такого результата следует увеличивать инерционность осциллятора (увеличивать массу ) и уменьшать жесткость упругого элемента до такой степени, что бы обеспечить выполнение неравенства 
. При этом масса практически не реагирует на возмущающее воздействие частоты 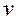, сохраняет свое положение неизменным и может выполнять роль неподвижной системы координат.
Рис. 4. Схема квазистатического прибора
Другую задачу решают квазистатические приборы, применяемые для измерения и регистрации как постоянных, так и переменных во времени сил (ускорений) или пропорциональных им величин. Примерами квазистатических приборов являются акселерометры – приборы, предназначенные для измерения ускорения, гироскопические датчики угловой скорости, гальванометры в осциллографах и многие другие. Схема прибора приведена на рис.4.
|
|
|
Уравнение движения такого прибора имеет вид:
. (8)
В идеальном случае квазистатический прибор должен обеспечивать пропорциональную зависимость между координатой x и измеряемой силой F(t). Для этого необходимо выполнение условий:
и 
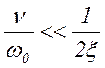. (9)
При 
достаточно обеспечить выполнение первого, а при 
второго требования (9).
Оба неравенства (9) для заданной частоты внешнего воздействия выполняются тем лучше, чем больше круговая частота собственных незатухающих колебаний 
. При этом а 
.
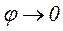Относительная динамическая погрешность квазистатического прибора может быть вычислена по формуле:
, (10)
а фазовая динамическая погрешность по формуле:
.
Т.о. приборы, состоящие из одних и тех же элементов и описываемые одинаковыми уравнениями, в зависимости от отношения частот, применяются для различных целей.
Программы FAZA и LAMBDA производят расчет соответственно фазового сдвига и коэффициента динамичности приборов в зависимости от отношения частот 
и 
(уравнения (3) и (4)).
Программа PRIBOR позволяет: 1) изменять физические параметры прибора; 2) изменять соотношение частот; 3) строить графики реакций на возмущающее воздействие квазистатического и сейсмического приборов; 4) получать числовые значения погрешностей квазистатического и сейсмического приборов.
Обозначения, принятые в программах:
tk – время интегрирования;
h – шаг интегрирования;
ksi – относительный коэффициент затухания собственных колебаний;
l – длина маятника;
m – масса маятника;
g – ускорение свободного падения;
j – осевой момент инерции маятника;
om0 – круговая частота собственных незатухающих колебаний;
nu – круговая частота внешнего возмущающего воздействия;
mfi – масштаб построения;
otn – максимальное значение отношения частот;
а – амплитуда возмущения;
voz – возмущающее воздействие;
i – текущее отношение частот;
t – текущее время;
y, teta, teta1, teta2, lam1, lam2, f11, f12, fidin1, fidin2, delta1, delta2 – переменные, используемые при расчетах и построениях;
Программа FAZA.
'ПОСТРОЕНИЕ ГРАФИКОВ СДВИГА ФАЗЫ
'*********************
SCREEN 12 'инициализация графического режима
'*********************
'********** заголовок графиков
LOCATE 1, 2
PRINT "Сдвиг фазы в зависимости от отношения частот и коэффициента ksi"
|
|
|
LOCATE 2, 10
PRINT "ksi изменяется от 0.1 до 1 с шагом 0.1"
'*********************
'*********************
mfi = 100 'масштаб построения
otn = 5 'максимальное значение отношения частот
'*********************
'************ вывод графической сетки с оцифровкой
LINE (20, 1)-(20, 420)
LINE (20, 420)-(630, 420)
LINE (20, 420 - 3.14 / 2 * mfi)-(630, 420 - 3.14 / 2 * mfi), 7
LINE (20, 420 - 3.14 * mfi)-(630, 420 - 3.14 * mfi), 7
LOCATE 17, 1: PRINT USING "#.##"; 3.14 / 2
LOCATE 7, 1: PRINT "3.14"
FOR y = 1 TO otn
LINE (20 + y * 120, 420)-(20 + y * 120, 420 - 3.14 * mfi), 7
LOCATE 28, 3 + 74 / 5 * y: PRINT y
NEXT y
LOCATE 28, 3: PRINT "0"
'********************
'*************** расчет и построение графиков
FOR ksi =.1 TO 1.001 STEP.1
FOR i = 0 TO otn STEP.002
fi = ATN((2 * ksi * i) / (1 - i ^ 2))
IF i > 1 THEN fi = 3.14 + ATN((2 * ksi * i) / (1 - i ^ 2))
PSET (20 + 120 * i, 420 - fi * mfi)
NEXT i
NEXT ksi
'*********************
END
Программа LANBDA
'ПОСТРОЕНИЕ ГРАФИКОВ КОЭФФИЦИЕНТА ДИНАМИЧНОСТИ
'***************************
SCREEN 12 'инициализация графического режима
'***************************
'********** заголовок графиков
LOCATE 1, 2
PRINT "Изменение коэффициента динамичности в зависимости от отношения частот и коэффициента ksi"
LOCATE 2, 10
PRINT "ksi изменяется от 0.1 до 1 с шагом 0.1"
'****************************
'****************************
mfi = 100 'масштаб построения для угла
otn = 5 'максимальное отношение частот
'****************************
'************ вывод графической сетки с оцифровкой
LINE (20, 1)-(20, 420)
LINE (20, 420)-(630, 420)
LINE (20, 420 - 1 * mfi)-(630, 420 - 1 * mfi), 7
FOR y = 1 TO otn
LINE (20 + 120 * y, 420)-(20 + 120 * y, 420 - 6 * mfi), 7
LOCATE 28, 3 + 74 / otn * y: PRINT y
NEXT y
LOCATE 28, 3: PRINT "0"
'****************************
'*************** расчет и построение графиков
FOR ksi =.1 TO 1.001 STEP.1
FOR i = 0 TO 5 STEP.002
lam = (i ^ 2) / SQR((1 - i ^ 2) ^ 2 + 4 * ksi ^ 2 * i ^ 2)
PSET (20 + 120 * i, 420 - lam * mfi)
NEXT i
NEXT ksi
'****************************
END
Программа PRIBOR
' ИССЛЕДОВАНИЕ СЕЙСМИЧЕСКОГО И КВАЗИСТАТИЧЕСКОГО ПРИБОРОВ
INPUT "Введите отношение частот "; otn
'*********************
tk = 2 'время интегрирования
h =.001 'шаг интегрирования
ksi =.5 'коэффициент затухания
l =.1 'длина маятника
m =.1 'масса груза
g = 9.8 'ускорение свободного падения
'*********************
'*********************
j = m * l ^ 2 'момент инерции
om0 = SQR(m * g * l / j) 'собственная частота нез. колебаний
nu = otn * om0 'частота вынуждающих колебаний
|
|
|
teta = 10 / 57 'начальный угол отклонения маятника
'*********************
'********************* построение координатных осей
SCREEN 12 'инициализация графического режима
FOR i = 0 TO tk STEP.5
LINE (640 / tk * i, 210)-(640 / tk * i, 230), 7
IF i <> 0 AND i <> tk THEN
LOCATE 16, i * INT(78 / tk): PRINT USING "#.##"; i
END IF
NEXT i
LINE (0, 220)-(640, 220)
LINE (0, 0)-(0, 440)
LOCATE 15, 74: PRINT "t [с]"
LOCATE 1, 2: PRINT "teta [рад]"
LINE (250, 395)-(350, 395), 12
LINE (250, 410)-(350, 410), 10
LINE (250, 425)-(350, 425), 11
LOCATE 25, 45: PRINT "реакция квазистатического прибора"
LOCATE 26, 45: PRINT "реакция сейсмического прибора"
LOCATE 27, 45: PRINT "возмущающее воздействие"
'*********************
'*********************
a = 10 / 57 'амплитуда возмущения
'коэффициент динамической восприимчивости
lam1 = (nu ^ 2 / om0 ^ 2) / SQR((1 - nu ^ 2 / om0 ^ 2) ^ 2 + 4 * ksi ^ 2 * nu ^ 2 / om0 ^ 2)
lam2 = 1 / SQR((1 - nu ^ 2 / om0 ^ 2) ^ 2 + 4 * ksi ^ 2 * nu ^ 2 / om0 ^ 2)
'фаза колебаний
fi1 = ATN((2 * ksi * (nu / om0)) / (1 - (nu ^ 2 / om0) ^ 2))
IF nu / om0 > 1 THEN fi1 = 3.14 + ATN((2 * ksi * (nu / om0)) / (1 - (nu ^ 2 / om0 ^ 2)))
fi2 = ATN((2 * ksi * nu * om0) / (om0 ^ 2 - nu ^ 2))
IF nu / om0 > 1 THEN fi2 = 3.14 + ATN((2 * ksi * nu * om0) / (om0 ^ 2 - nu ^ 2))
'амплитудная погрешность
delta1 = ABS(1 - lam1) * 100
delta2 = ABS(1 - lam2) * 100
fidin1 = -3.14 + fi1 'фазовая погрешность
fidin2 = -1 * fi2
'*********************
'********************* решение уравнения
FOR t = 0 TO tk STEP h
'возмущающее воздействие
voz = a * COS(nu * t)
'аналитическое решение уравнения
teta1 = a * lam1 * COS(nu * t - fi1)
teta2 = a * lam2 * COS(nu * t - fi2)
PSET (640 / tk * t, 220 - teta1 * 500), 10
PSET (640 / tk * t, 220 - teta2 * 500), 12
PSET (640 / tk * t, 220 - voz * 500), 11
NEXT t
'*********************
'********************* вывод на экран числовой информации
LOCATE 1, 47: PRINT "сейсмический"
LOCATE 1, 65: PRINT "квазистатический"
LOCATE 2, 2: PRINT "круговая частота собственных"
LOCATE 3, 2: PRINT "незатухающих колебаний, om0[1/c]"
LOCATE 4, 2: PRINT "круговая частота вынуждающих колебаний, nu[1/c]"
LOCATE 5, 2: PRINT "коэффициент динамической"
LOCATE 6, 2: PRINT "восприимчивости, lam"
LOCATE 7, 2: PRINT "амплитудная погрешность, delta[%]"
LOCATE 8, 2: PRINT "фаза колебаний, fi[град]"
LOCATE 9, 2: PRINT "фазовая погрешность, fidin[град]"
LOCATE 3, 50: PRINT USING "##.##"; om0
LOCATE 4, 50: PRINT USING "##.##"; nu
LOCATE 6, 50: PRINT USING "#.######"; lam1
LOCATE 7, 50: PRINT USING "##.###"; delta1
LOCATE 8, 50: PRINT USING "###.#"; fi1 * 57
LOCATE 9, 50: PRINT USING "####.###"; fidin1 * 57
LOCATE 3, 65: PRINT USING "##.##"; om0
LOCATE 4, 65: PRINT USING "##.##"; nu
LOCATE 6, 65: PRINT USING "#.######"; lam2
LOCATE 7, 65: PRINT USING "##.###"; delta2
LOCATE 8, 65: PRINT USING "###.#"; fi2 * 57
LOCATE 9, 65: PRINT USING "####.###"; fidin2 * 57
'*********************
END
3. Объект исследования.
Объектом исследования являются цифровые модели квазистатического и сейсмического приборов.
4.Последовательность проведения работы.
4.1. Изучить теоретические основы.
4.2. Изучить программы FAZA, LAMBDA и PRIBOR.
4.3. Используя программу FAZA, построить графики сдвига фазы для 
=0.5…0.9. Занести их в отчет.
4.4. Используя программу LAMBDA, построить графики коэффициента динамичности для =0.5…0.9. Занести их в отчет.
|
|
|
4.5. Исследуя полученные графики сдвига фазы и коэффициента динамичности, выбрать наилучшее с точки зрения теории колебаний значение .
4.6. Получить у преподавателя значения массы и длины маятника в соответствии со своим вариантом.
4.7. Ввести в программу PRIBOR значения выбранного , а так же заданных – массы и длины маятника.
4.8. Используя программу PRIBOR, найти интервал для частоты внешнего возмущающего воздействия, в котором прибор с данными характеристиками можно использовать в качестве сейсмографа с динамической погрешностью измерения амплитуды не более 1%.
4.9. Используя программу PRIBOR, найти интервал для частоты внешнего возмущающего воздействия, в котором прибор с данными характеристиками можно использовать в качестве измерителя силы (квазистатический прибор) с динамической погрешностью измерения амплитуды не более 1%.
4.10. Занести результаты в отчет и сделать вывод по проделанной работе.
5. Контрольные вопросы.
5.1. Что общего и различного в квазистатическом и сейсмическом приборах.
5.2. Что характеризует и от каких параметров зависит коэффициент динамичности.
5.3. Из каких соображений необходимо выбирать частоту собственных незатухающих колебаний сейсмического (квазистатического) прибора.
6. Библиографический список.
6.1. Савельев В.В. Прикладная теория колебаний: Учебн. пособ. – Тула: ТулГУ. – Тула, 2005. – 160 с.
|
|
|
