 |
Построение фазовых траекторий
|
|
|
|
Нелинейных систем
1. Цель работы.
Научится строить фазовые траектории и качественно определять по ним процессы, протекающие в системах.
2. Основы теории.
Фазовой плоскостью называют плоскость, обозначенную системой прямоугольных координат, когда по одной оси откладывается координата, определяющая значение колеблющейся величины, а по другой оси – значение скорости изменения этой величины. Каждому состоянию рассматриваемой колебательной системы соответствует точка на фазовой плоскости, которая называется изображающей точкой. При движении колебательной системы будет происходить изменение координаты и скорости и, следовательно, изображающая точка будет перемещаться по некоторой кривой, которую принято называть фазовой траекторией.
Фазовая плоскость используется для наглядного изображения колебательного движения рассматриваемой системы. В ряде случаев, особенно при исследовании нелинейных колебательных систем, построение фазовых траекторий является единственным способом хотя бы качественно оценить процессы, происходящие в изучаемой системе. Начальные условия процессов определяют координаты начальной точки фазовой траектории. Размеры фазовых траекторий (по колеблющейся величине и ее скорости) зависят от амплитуды колебаний.
Фазовые траектории устойчивой линейной системы будут асимптотически приближаться к началу координат при неограниченном увеличении времени. Фазовые траектории неустойчивой линейной системы будут неограниченно удаляться от начала координат.
Для нелинейной системы фазовые траектории могут принимать самые разнообразные очертания.
В качестве примера изобразим на фазовой плоскости переходный процесс и автоколебания в системе автоматического регулирования температуры.
|
|
|
Рис. 1. Автоматический регулятор температуры с релейным элементом
Автоматический регулятор температуры представляет собой релейную систему (рис. 1). Релейной эту систему называют потому, что для управления работой привода шторок в ней поставлено релейное звено – поляризованное реле 3. Его средний контакт в зависимости от знака тока в диагонали моста 2, т.е. в зависимости от знака регулируемой величины q, замыкается с правым или левым контактом, включая ток либо в одну, либо в другую обмотку возбуждения двигателя, в результате чего получается либо одно, либо другое направление движения шторок на регулируемом объекте.
Из сети в управляемую цепь реле (цепь контактов) подается постоянное напряжение U = с. Напряжение U, питающее двигатель, изменяется в зависимости от величины тока I в диагонали моста по закону, изображенном на рис.2. Это характеристика идеального реле (без зоны застоя) с гистерезисной петлей. Гистерезисная петля возникает в результате несовпадения величины тока срабатывания и величины тока отпускания реле.
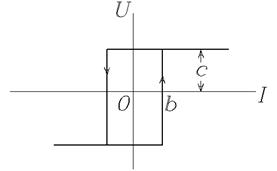
Рис. 2.Статическая характеристика реле
Составим сначала уравнение регулируемого объекта и регулятора. Пусть регулируемый объект представляет собой некоторую камеру. Учитывая инерционность процесса нагрева и охлаждения, запишем уравнение регулируемого объекта в виде
, (1)
где q - отклонение температуры, j - отклонение регулирующего органа, T1 – постоянная времени системы, k1 – коэффициент передачи, f(t) – внешнее возмущение.
При отклонении температуры q появляется ток в диагонали моста того или иного направления (рис. 1) и замыкает тот или иной контакт реле 3, включающего постоянное напряжение в ту или иную обмотку возбуждения 4 электродвигателя 5. Считая, что ток I пропорционален отклонению температуры объекта q, а скорость 
отклонения регулирующего органа 6 пропорциональна напряжению на обмотках возбуждения электродвигателя, можно в данном случае выходной величиной для релейной характеристики считать прямо , а выходной - q (рис. 3).
|
|
|
Рис.3. Статическая характеристика реле в новых обозначениях
Следовательно, уравнение регулятора запишется следующим образом:
; (2)
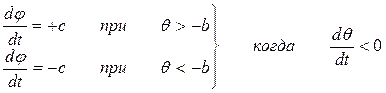. (3)
Рассмотрим два произвольных участка переходного процесса (при f(t) = 0) – участки AB и BD (рис. 4).
На участке AB уравнение регулятора будет 
. Дифференцируя (1) по t и подставляя туда +с, получаем при f(t) = 0 следующее уравнение системы регулирования на участке AB:
, (4)
а на участке BD
. (5)
Рис.4. К составлению уравнения работы автоматического регулятора температуры
Для построения фазовой траектории введем координаты фазовой плоскости
и 
. (6)
Рис.5. Семейство фазовых траекторий автоматической системы регулирования температуры с релейным элементом, отвечающих различным начальным условиям
Если у > 0, то согласно (2) и рисункам 3, 4 переключение регулятора происходит при q = +b (линия EF на рис. 5); если же y < 0, то при q = - b (линия GH). Справа от линии переключения EFGH справедливо уравнение (4), а слева – (5).
Уравнение (4) в обозначениях (6) примет вид
. (7)
Семейство кривых, отвечающих различным начальным условиям x(0) и y(0), изображено на рис.5 справа от линии EFGH. Эти кривые имеют асимптоту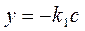 
. Движение изображающей точки по ним происходит по ходу часовой стрелки, т.е. x возрастает при y > 0 и убывает при y < 0.
Уравнение (5) в обозначениях (4) примет вид
. (8)
Соответственно семейство кривых для различных начальных условий находится слева от линии EFGH.
В результате получается, что амплитуда расходящихся колебаний увеличивается (уменьшатся) только до определенного значения, а затем остается постоянной. Т.е. фазовые траектории расходятся от начала координат и сходятся из бесконечности до так называемого предельного цикла.
Следовательно, в данной системе автоматического регулирования будут наблюдаться устойчивые автоколебания, к которым сходится переходный процесс с обеих сторон, т.е. при любых начальных условиях.
Автоколебательный процесс является здесь единственно возможным видом установившегося процесса, а строгое поддержание постоянной температуры невозможно. Амплитуда автоколебаний температуры в данной системе регулирования изображается на рис.5 отрезком а. Отрезок g изображает амплитуду скорости изменения температуры при автоколебаниях.
|
|
|
Таким образом, решая (любым численным методом) уравнения (7) и (8) при учете условий (2) и (3) (моделирование работы релейного элемента) можно получить цифровую модель нелинейной автоколебательной системы и построить по ней фазовую траекторию. Изучая фазовую траекторию, можно качественно оценить процессы, протекающие в системе с данными параметрами (постоянной времени, коэффициентом передачи и т.д.).
Программа TRAEKTORIA позволяет строить фазовые траектории автоматической системы регулирования температуры, изображенной на рис.1 с релейным элементом, статическая характеристика которого изображена на рис.2 при различных параметрах самой системы и различных начальных условиях (начальной температуры и скорости ее изменения).
3. Объект исследования.
Объектом исследования является цифровая модель автоматического регулятора температуры с релейным элементом.
4.Последовательность проведения работы.
4.1. Изучить теоретические основы.
4.2. Изучить программу TRAEKTORIA.
4.3. Получить у преподавателя значения параметров системы и начальные условия.
4.4. Используя программу TRAEKTORIA построить фазовую траекторию системы. График фазовой траектории занести в отчет по работе.
4.5. Сделать выводы по проделанной работе (качественно описать процесс изменения температуры на регулируемом объекте и его зависимость от параметров системы и начальных условий).
5. Контрольные вопросы.
5.1. Что такое фазовая плоскость и фазовая траектория?
5.2. Какие параметры процессов, протекающих в системе можно оценить по фазовой траектории?
5.3. Что представляет собой фазовая траектория линейного осциллятора с затуханием (без затухания, с расхождением)?
6. Библиографический список.
6.1. Савельев В.В. Прикладная теория колебаний: Учебн. пособ. – Тула: ТулГУ. – Тула, 2005. – 160 с.
|
|
|
Перечень оборудования.
|
|
|
