 |
Изучение колебательных процессов
|
|
|
|
НА КОМПЬЮТЕРЕ
1.Цель работы.
Изучение собственных колебаний осцилляторов на компьютере.
2. Основы теории.
Уравнение движения осциллятора (масса на пружине) имеет вид:
, (1)
где 
- перемещение, скорость и ускорение осциллятора; 
- масса осциллятора; 
- коэффициент демпфирования;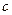 
- жесткость пружины; 
- возмущающее воздействие.
Поделив уравнение на коэффициент при старшей производной, получим:
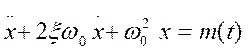, (2)
где 
– относительный коэффициент демпфирования колебаний осциллятора: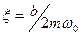 
; 
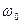– круговая частота собственных незатухающих колебаний осциллятора: 
; 
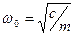– относительное возмущающее воздействие: 
.
Важным при создании реальных колебательных систем является вопрос выбора коэффициента демпфирования . Идеальным для квазистатических приборов является значение 
при этом обеспечивается значительное уменьшение амплитуды колебаний (в 
раз за один период), и незначительно увеличивается период затухающих колебаний по сравнению с периодом незатухающих колебаний (в 
раза). Выбор значения коэффициента демпфирования зависит от конкретных условий эксплуатации и требований, предъявляемых к системе.
Уравнение (2) является дифференциальным уравнением второго порядка, для решения которого численным методом в ЭВМ его необходимо привести к канонической форме (системе уравнений первого порядка).
Для этого запишем (2) в виде:
. (3)
Обозначим:
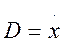. (4)
Тогда уравнение (3) можно переписать в виде:
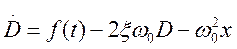. (5)
Уравнения (4) и (5) представляют собой систему двух дифференциальных уравнений первого порядка, интегрируя которые по времени, можно получить значение перемещения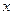 
.
Исследуем движение осциллятора при наличии начального отклонения 
. Тогда:
|
|
|
, (6)
при условии
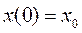, (7)
где - начальное отклонение осциллятора.
Существуют различные методы численного интегрирования дифференциальных уравнений (метод прямоугольников, метод трапеций, метод Симпсона, метод Рунге-Кутта и др.), выбор которых для решения конкретных задач, зависит от требуемой точности и затрат машинных ресурсов.
Сущность метода интегрирования прямоугольниками (метода Эйлера с постоянным шагом) иллюстрируется рисунком 1.
 |
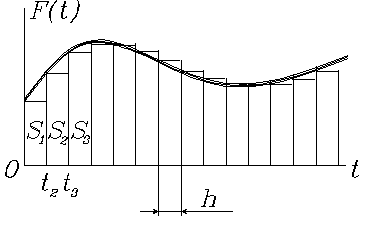Рис. 1. Метод прямоугольников
Интеграл от функции равен сумме площадей прямоугольников (S1, S2, S3 и т.д.), где площадь прямоугольника Si равна произведению значения функции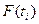 
на шаг интегрирования h.
 |
Более точным методом является метод трапеций. При этом интеграл от функции
равен сумме площадей трапеций (рис.2).
Рис.2. Метод трапеций
Шаг интегрирования h следует выбирать исходя из необходимой точности и требований к затратам машинных ресурсов. При увеличении шага интегрирования потребуется меньше машинных ресурсов, однако, точность интегрирования уменьшится. При уменьшении шага h точность расчетов возрастает, и, соответственно, увеличиваются затраты машинных ресурсов. Следует знать, что для методов прямоугольников и трапеций при увеличении шага интегрирования решение может потерять устойчивость. Выбор верхней границы для значения шага h зависит от параметров прибора и условий движения. Например, в случае свободных затухающих колебаний осциллятора скорость 
изменяется с частотой собственных затухающих колебаний 
. Если h больше 
, то (рис. 3.а) суммируемые площади будут находиться или в положительной или в отрицательной области. При этом модуль суммы площадей будет накапливаться, и решение потеряет устойчивость.
Следовательно, для того, что бы решение не потеряло устойчивость, должно выполняться условие: 
,
или
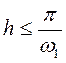. (8)
При этом (рис. 3.б) за один период изменения скорости суммируются две площади: одна из положительной области, другая – из отрицательной. В этом случае потери устойчивости решения не происходит.
|
|
|
 |
а) б)
Рис. 3. К выбору шага интегрирования
Программа MAYATNIK предназначена для решения системы (6) при условии (7) методами прямоугольников и трапеций.
В программе приняты следующие обозначения:
tk – время интегрирования;
h – шаг интегрирования;
demp – демпфирование;
ksi – относительный коэффициент затухания собственных колебаний;
d, d1, d2- переменные, используемые при интегрировании;
m – масса осциллятора;
с – жесткость упругого элемента;
om0 – круговая частота собственных незатухающих колебаний;
om1 – круговая частота затухающих колебаний;
teta, teta1, teta2 – отклонения осциллятора от начального положения.
Программа MAYATNIK
' ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ МАЯТНИКА
'************* входные данные
tk = 1 'время интегрирования
demp =.7 'коэффициент демпфирования
m =.1 'масса осциллятора
с = 10 ‘жесткость упругого элемента
teta = 10 / 57 'начальное отклонение осциллятора
'для метода прямоугольников
teta2 = teta 'начальное отклонение осциллятора
'для метода трапеций
d = 0: d1 = 0: d2 = 0 'обнуление переменных, используемых
'при численном интегрировании
'*********************
'*************** расчет параметров маятника
om0 = SQR(с/ m) 'круговая частота собственых нез. Колебаний
ksi = demp/(2*m*om0) ‘относительный коэффициент демпфирования
om1 = om0 * SQR(1 - ksi ^ 2) 'круговая частота затухающих колебаний
'*********************
h = (3.14 / om1) / 50 'шаг интегрирования
'********************* построение координатных осей
SCREEN 12 'инициализация графического режима
FOR i = 0 TO tk STEP.5
LINE (640 / tk * i, 210)-(640 / tk * i, 230), 7
IF i <> 0 AND i <> tk THEN
LOCATE 16, i * INT(78 / tk): PRINT USING "#.##"; i
END IF
NEXT i
LINE (0, 220)-(640, 220)
LINE (0, 0)-(0, 440)
LOCATE 15, 74: PRINT "t [с]"
LOCATE 1, 2: PRINT "teta [рад]"
'*********************
'********************* вывод на экран числовой информации
LINE (260, 1)-(585, 210),, B
LOCATE 2, 35: PRINT USING "коэффициент затухания ksi=#.#"; ksi
LOCATE 3, 35: PRINT USING "масса маятника m=##.## [кг]"; m
LOCATE 4, 35: PRINT USING "масса маятника demp=##.##"; demp
LOCATE 5, 35: PRINT USING "жесткость упругого элемента с=##.##"; с
LOCATE 6, 35: PRINT "круговая частота собственных"
LOCATE 7, 35: PRINT USING "незатухающих колебаний om0=##.## [1/с]"; om0
LOCATE 8, 35: PRINT "круговая частота"
|
|
|
LOCATE 9, 35: PRINT USING "затухающих колебаний om1=##.## [1/с]"; om1
LOCATE 10, 35: PRINT "начальное"
LOCATE 11, 35: PRINT USING "отклонение осциллятора teta=##.## [град]"; teta * 57
LOCATE 12, 35: PRINT USING "время интегрирования tk=## [c]"; tk
LOCATE 13, 35: PRINT USING "шаг интегрирования h=#.##### [c]"; h
'*********************
'********************* решение уравнения
FOR t = 0 TO tk STEP h
ch = ch + 1
'*** методом прямоугольников
d = d + h * (-2 * ksi * om0 * d - om0 ^ 2 * teta)
teta = teta + h * d
'*** методом трапеций
d1 = d2 + h / 2 * ((-2 * ksi * om0 * d1 - om0 ^ 2 * teta1) + (-2 * ksi * om0 * d2 - om0 ^ 2 * teta2))
teta1 = teta2 + h / 2 * (d1 + d2)
d2 = d1
teta2 = teta1
'***** построение графика
PSET (640 / tk * t, 220 - teta * 500), 10
PSET (640 / tk * t, 220 - teta1 * 500), 12
NEXT t
'*********************
END
3. Объект исследования.
Объектом исследования является цифровая модель математического маятника.
4.Последовательность проведения работы.
4.1. Изучить теоретические основы.
4.2. Изучить программу MAYATNIK.
4.3. Получить у преподавателя значения масс двух осцилляторов (
и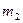 
) и жестокостей их пружин (
и 
) в соответствии со своим вариантом.
4.4. Ввести в программу значения массы и жесткости пружины первого осциллятора.
4.5. Используя программу, построить графики колебаний осциллятора, задаваясь различными значениями такими, что бы находился в диапазоне 0,1…0,9. Графики, исходные данные (, , , 
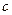) и результаты расчетов (, , 
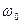) занести в отчет по работе.
4.6. Повторить пункт 4.5. для второго осциллятора с массой 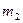и жесткостью .
4.7. Заполнить таблицу.
Таблица.
| первый осциллятор | второй осциллятор | ||
| m1 =________, c1 =___________ | m2 =________, c2 =___________ | ||
| d | x | d | x |
| … | … | … | … |
4.8. Сделать вывод по результатам проведенной работы.
5. Контрольные вопросы.
5.1. На какие характеристики осциллятора влияет демпфирование?
5.2. Как результат интегрирования зависит от шага интегрирования?
5.3. Как влияет изменение параметров маятника (массы и длины) на период затухающих колебаний?
6. Библиографический список.
6.1. Савельев В.В. Прикладная теория колебаний: Учебн. пособ. – Тула: ТулГУ. – Тула, 2005. – 160 с.
|
|
|
