 |
5. Регресионные модели временных рядов
|
|
|
|
5. Регресионные модели временных рядов
и прогнозирование
5. 1. Структура и классификация временных рядов
Временным (динамическим) рядом называется последовательность значений (уровней) переменной, измеренной в последовательные моменты времени: уt (t=1, 2,..., n), где n - длина ряда (число уровней).
В структуре экономических временных рядов в общем случае выделяют четыре составляющих (слагаемых):
| уt = ut +nt +ct +et, | (5. 1) |
| где | ut | - тренд, отражает основную долговременную тенденцию изменения признака – явления; |
| nt | - сезонная составляющая, отражает цикличность изменения значений признака на внутренних относительно небольших (микро- и мезоуровнях) интервалах наблюдения (неделя, месяц, время года и т. п.; | |
| ct | - циклическая компонента, отражает цикличность изменения значений признака на внутренних больших интервалах наблюдения (макроуровнях) типа циклов солнечной активности Чижевского, волн Кондратьева, демографических ям и т. п.; | |
| et | - случайная составляющая, отражает влияние не поддающихся учету случайных факторов. |
Первые три составляющие являются неслучайными, закономерными. Поэтому полной задачей анализа временного ряда является выявление всех этих трех закономерностей. Частной задачей может быть выявление какой-либо пары закономерностей из трех - это зависит от особенностей ряда и цели исследования.
Однако не всегда ряды содержат все три неслучайных составляющих, либо они пренебрежимо малы, либо их оценка невозможна ввиду ограниченности статистического материала, либо, наконец, это не диктуется целью исследования.
|
|
|
Классической задачей анализа временных рядов является выявление одной главной закономерности - тренда.
Наиболее распространенные методы исследования: корреляционный и спектральный анализы, модели авторегрессии и скользящей средней.
Важнейшей классификацией временных рядов (процессов) является их деление на стационарные и нестационарные. Временной ряд уt (t=1, 2,..., n) называется строго стационарным (или стационарным в узком смысле), если совместное распределение вероятностей n наблюдений у1+t, у2+t, ... , уn+t не зависит от n, t и временного сдвига t. Поэтому характеристики распределения МО ay(t)=а, СКО sy(t)=s можно оценить на основе наблюдений уt (t=1, 2,..., n) по формулам:
 , ,
| (5. 2) |
 . .
| (5. 3) |
Классическим стационарным рядом в узком смысле является случайный процесс типа " белый шум", у которого МО ay(t)=0, а возмущения et некоррелированы между собой. Таким образом, возмущения et в классической линейной регрессионной модели образуют белый шум, а в случае их нормального распределения - нормальный белый шум.
Временной ряд уt (t=1, 2,..., n) называется стационарным (в широком смысле), если лишь числовые характеристики совместного распределения вероятностей n наблюдений у1+t, у2+t, ... , уn+t не зависят от n, t и временного сдвига t. Содержательно стационарный ряд отражает процесс эволюции наблюдаемого явления.
При нарушении условия постоянства числовых характеристик временной ряд называется нестационарным. Нестационарный ряд отражает переход из одного устойчивого состояния в другое - развитие (деградация), у него есть начало и конец. Стационарный ряд может быть одной из составляющих нестационарного ряда.
5. 2. Автокорреляционная функция
Важной характеристикой временных рядов является автокорреляционная функция r. Для стационарных рядов она зависит только от одной неслучайной переменной - временного сдвига (лага) t, для нестационарных - от двух переменных: сдвига (лага) t и момента начала отсчета t. Автокорреляционная функция определяется аналогично коэффициенту корреляции:
|
|
|
 . .
| (5. 4) |
Статистической оценкой r(t) является выборочная автокорреляционная функция r(t). График этих функций называют коррелограммой:
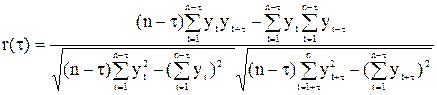 . .
| (5. 5) |
Свойства автокорреляционной функции (рис. 5. 1):
1. r(t)=r(-t) - функция четная.
2. r(t=0)=1.
3. При t®¥ ç r ç ®0.
| r | 
| |||||
 1 1
| 
| |||||
  
| ||||||
 
| 
| |||||

|      
| |||||

|   3 4 3 4
|  5 5
| 
| |||
| 1 2 |   
| 
| 6 7 | 
| t | |

|
|
|
|


