 |
6.3. Сущность и последствия гетероскедастичности
|
|
|
|
6. 3. Сущность и последствия гетероскедастичности
Равенство дисперсий возмущений ei регрессии - гомоскедастичность - является обязательным условием линейной классической модели. Формально оно записывается в виде: å e=s2En.
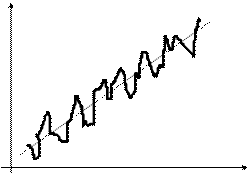
Однако на практике это условие часто нарушается, и мы имеем дело с гетероскедастичностью. В парной регрессии это может проявляться так: с ростом объясняющей переменной Х растет в среднем значение результирующей переменной Y и одновременно увеличивается разброс точек относительно тренда (рис. 6. 1 и 6. 2).

| |||||||||
 y y
| y | ||||||||
| x | x |
Рис. 6. 1. Явление гомоскедастичности Рис. 6. 2. Явление гетероскедастичности
Рассмотрим последствия гетероскедастичности. Пусть для оценки регрессии Y по Х1, ... , Хp мы применили обычный МНК и получили оценочный вектор b для вектора параметров b: b=(X’X)-1X’Y. Если вместо Y подставить его модель Y=Xb+e, то после несложных преобразований получим (заметим, что вектор b зависит от случайного вектора e):
|
|
|
| b=(X’X)-1X’Y=b+(X’X)-1X’e. | (6. 11) |
Эта оценка - несмещенная и состоятельная для обобщенной линейной модели множественной регрессии, в том числе для случая гетероскедастичности (это очевидно, если учесть М(e)=0). Следовательно, для построения регрессионной модели и использования ее в качестве прогностического инструмента обычный метод наименьших квадратов применим и в случае гетероскедастичности модели.
Неприятности начинаются, когда мы хотим оценить точность модели, ее значимость, получить интервальные оценки ее коэффициентов. Результаты оказались бы непригодными.
Дело в том, что при расчете t- и F-статистик для тестирования гипотез важное значение имеют оценки дисперсий и ковариаций оценок bi, т. е. ковариационная матрица å b. Если модель не является классической, то ковариационная матрица вектора возмущений å e¹ s2En, и вместо å b=s2(X’X)-1 мы имеем существенно иную ковариационную матрицу:
å b = (X’X)-1X’WX(X’X)-1.
Добавим также, что несмещенная и состоятельная оценка в случае гетероскедастичности не будет оптимальной в смысле теоремы Гаусса-Маркова, т. е. эффективной. Это может привести к тому, что оценка b будет значительно отличаться от истинного значения b.
6. 4. Тесты на гетероскедастичность
Для проверки наличия или отсутствия гетероскедастичности используются тесты. Соответствующая нулевая гипотеза Но: гетероскедастичность отсутствует (присутствует гомоскедастичность).
Тест ранговой корреляции Спирмена использует следующую идею. Модули остатков ç еiç являются оценками СКО si, поэтому при гетероскедастичности модули остатков ç еiç и значения регрессоров xi будут коррелированы.
Коэффициент ранговой корреляции рассчитывается по формуле:
 , ,
| (6. 12) |
где di - разность между рангами значений xi и ei.
|
|
|
Коэффициент ранговой корреляции значим на уровне значимости a, если выполняется условие:
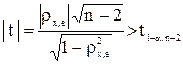 , ,
| (6. 13) |
где t1-a, n-2 - табличное значение t-критерия Стьюдента с уровнем значимости a и числом степеней свободы (n-2).
Тест Голдфелда-Квандта можно применять тогда, когда ошибки регрессии имеют НЗР. Пусть средние квадратические отклонения ошибок si пропорциональны значениям переменной Х (постоянство относительного, а не абсолютного разброса возмущений). Упорядочим наблюдения в порядке возрастания Х и выберем m первых и m последних наблюдений (две m-выборки).
Гипотеза Но о наличии гомоскедастичности будет равносильна утверждению о том, что две нормально распределенные m-выборки имеют одинаковые дисперсии.
Гипотеза о равенстве дисперсий по критерию Фишера-Снедекора отвергается, если выполняется неравенство:
 . .
| (6. 14) |
Мощность теста оказывается максимальной, если выбирать m»n/3.
Тест Уайта в отличие от двух рассмотренных выше тестов позволяет проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров. Для этого предполагается, что существует функция, которая свяжет дисперсии ошибок с регрессорами. Обычно в качестве таковой берется квадратичная функция:
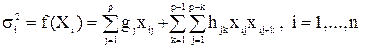 . .
| (6. 15) |
После выбора вида функции последняя оценивается с помощью уравнения регрессии для квадратов остатков:
| еi2 =f(Хi) + ui, i=1, ... , n, | (6. 16) |
где ui - ошибка регрессии в i-м наблюдении.
Гипотеза об отсутствии гетероскедастичности (условие f=const) принимается, если регрессия (6. 16) незначима.
|
|
|


