 |
4.6. Производственная функция Кобба-Дугласа
|
|
|
|
4. 6. Производственная функция Кобба-Дугласа
В качестве примера линеаризующего преобразования рассмотрим одну из многих типов производственных функций - функцию Кобба-Дугласа:
 = AKaLb,
| (4. 4) |
где Y - объем производства,
К - затраты капитала,
L - затраты труда,
a и b - коэффициенты частной эластичности Y по К и L: ЕК(Y)=a, ЕL(Y)=b.
С учетом влияния возмущений функция Кобба-Дугласа может выглядеть как мультипликативная степенная модель:
| Y = AKaLbe. | (4. 5) |
Эту модель можно свести к линейной относительно параметров путем логарифмирования обеих частей:
| lnY = lnA+alnK+blnL+lne. | (4. 6) |
Если в формуле (4. 5) принять, что при увеличении затрат К и L на расширение масштабов производства в несколько раз объем производства возрастает в такое же число раз, то a+b=1 и функция Кобба-Дугласа примет вид: Y = AKaL1-ae или:
| Y/L = A∙ (K/L) ae, | (4. 7) |
где Y/L - производительность труда (руб. /чел. за год),
K/L - капиталовооруженность (руб. /чел. в среднем за год).
Для оценки параметров модели (4. 7) ее нужно прологарифмировать.
Еще один вариант функции Кобба-Дугласа учитывает фактор экспоненциального роста технического прогресса:
| Y = AKaLbeqte, | (4. 8) |
где t - время, а q - темп прироста объема производства вследствие технического прогресса. Эта модель также приводится к линейному виду путем логарифмирования.
4. 7. Частные коэффициенты корреляции
Часто возникает необходимость исследовать частную корреляцию между переменными при исключении - элиминировании - влияния остальных переменных. Выборочный частный коэффициент корреляции между переменными Хi и Xj при фиксированных остальных р-2 переменных определяется выражением:
|
|
|
ri-j, 1, 2,..., p =  ,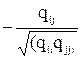
| (4. 9) |
где qii и qjj - алгебраические дополнения элементов rii и rjj матрицы коэффициентов корреляции (для частного случая р=3):
 .
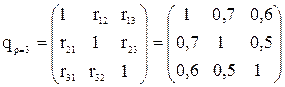| (4. 10) |
Пример 4. 4.
Записать выражение (4. 9) для случая трех переменных (р=3) относительно частного коэффициента корреляции r1-2, 3 и вычислить его значение на основе корреляционной матрицы (4. 10).
Решение.
Построим алгебраические дополнения на основе матрицы (4. 10), а затем и само выражение (i=1, j=2, k=3):
q11=+(1-  )=0, 75
| q22=+(1-  )=0, 64
| q12= -(r12- r13 r23)=-0, 40 |
 .
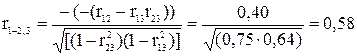| (4. 11) |
Если взять значения коэффициентов корреляции r12=0, 6; r13= r23=0, 8, то получим отрицательное значение частного коэффициента корреляции: r1-2,. 3=-0, 11.
Смысл частного коэффициента можно получить из следующих рассуждений. Пусть имеется уравнение регрессии х1=bо+b1х2+b2х3+e. Требуется оценить корреляцию между Х1 и Х2 при исключении влияния Х3.
Для решения найдем два уравнения регрессии:
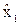=bо+b1х3 и 
= 
+ 
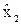х3.
Коэффициент корреляции между остатками 
и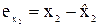 
отражает тесноту частной корреляции между переменными Х1 и Х2.
Таким образом, обычный коэффициент корреляции между остатками равен частному коэффициенту между самими переменными.
Как и обычный, частный коэффициент корреляции принимает значения от -1 до +1.
Значимость частного коэффициента корреляции ri-j, 1, 2,..., p оценивается так же, как и обычного коэффициента r, полагая объем выборки n’=n-p+2.
Вопросы для самоконтроля
1. Какие алгебраические и содержательные неприятности влечет высокая мультиколлинеарность?
2. Как выявляют и уменьшают степень мультиколлинеарности по матрице парных коэффициентов корреляции?
3. В чем суть метода отбора значащих факторов и уменьшения мультиколлинеарности методом вращения факторов?
4. Сколько нужно построить уравнений регрессий и вычислить оценок остаточной дисперсии s2 при отборе факторов методом вращения для исходного уравнения с четырьмя объясняющими переменными?
|
|
|
5. Приведите произвольный исходный числовой пример для метода Чоу с двумя парами выборок.
6. Нарисуйте бинарное дерево классификации регрессии.
7. К какому классу нелинейности относится регрессия
у = bо+ b1 / x + e?
8. Приведите степенную функцию: у = bо xb1e к линейному виду. К какому классу нелинейностей относится эта функция?
9. Что означает “средний коэффициент эластичности”?
10. У какой функции регрессии функция эластичности есть константа?
11. Какой смысл и какие размерности имеют переменные и параметры функции Кобба-Дугласа? Получите сами значения частных коэффициентов эластичности этой функции.
12. Что называется элиминированием переменных?
13. В чем смысл частного коэффициента корреляции?
|
|
|
