 |
Рис. 4.1. Схема отбора значимых факторов
|
|
|
|
Рис. 4. 1. Схема отбора значимых факторов
Картина резко меняется, если поступить иначе. Отбираем самый информативный фактор на 1-е место. Для этого строим шесть парных регрессий и для каждой вычисляем остаточную дисперсию s2. В искомое уравнение включаем тот фактор, у которого наименьшая дисперсия s2. В нашем примере это Хс. Далее ищем второй по значимости фактор. Для этого строим пять регрессий с парами факторов, один их которых присутствует всегда - Хс. Для каждой такой регрессии также вычисляем остаточные дисперсии s2. В примере наименьшую дисперсию дает фактор Хе, и т. д.
В работе [5, с. 111] в подобной процедуре в качестве критерия используется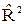 
- скорректированный коэффициент детерминации.
Вывод: факторы по значимости резко разделились на две группы. Из шести мы отобрали три фактора, которые в совокупности дают небольшую дисперсию ошибки и практически полностью исключают коллинеарность. Заметим, что полное ее исключение обычно и не является целью исследования.
4. 2. Линейные регрессионные модели с атрибутивными факторами
Ранее мы имели дело только с количественными показателями. В практике исследований часто встречаются и качественные - атрибутивные - объясняющие переменные. Например, показатель пол имеет два значения (булевская переменная). Показатели образование, сезон, способ производства имеют по нескольку значений. Конечно, в случае с полом можно построить отдельно регрессию для мужчин и отдельно для женщин (подробнее см. 4. 3 - критерий Чоу). Но если значений атрибутивной переменной несколько, то обычно не хватает выборочных данных при их расчленении.
Более конструктивный подход связан с включением атрибутивных переменных в уравнение регрессии, наделив их условными числовыми значениями. Отсюда и название - фиктивные переменные. Например, пусть для женщин z1=0, для мужчин z1=1. (Значения 0 и 1 более удобны, чем другие, например, 2 и 3).
|
|
|
Для показателя “образование” можно взять несколько значений: 1 - среднее, 2 - среднее профессиональное, 3 - высшее. Однако при таком подходе могут возникнуть трудности содержательной интерпретации коэффициентов регрессии.
Поэтому обычно вместо k=3 значений вводят k-1=2 булевских переменных. Покажем табличную (табл. 4. 1) формальную процедуру их введения: таблицу нужно заполнять единицами так, чтобы в каждой строке была только одна 1.
Таблица 4. 1
Включение булевских переменных в регрессию
| Среднее | Среднее проф | Высшее | Итого | |
| Z1 | ||||
| Z2 |
На основе этой таблицы легко выписать смысл значения булевских переменных: z1=1, если высшее и z1=0 иначе; z2=1, если среднее профессиональное и z2=0 иначе; если z1=0 и z2=0, то среднее (другого не дано).
4. 3. Критерий Чоу: объединение регрессий
Пусть Y - среднемесячная зарплата (руб. ), Х - продолжительность образования (лет). Пусть у нас имеются две пары выборок Y и Х объемами n1 и n2: одна пара - для мужчин, другая - для женщин. Вопрос: можно ли объединить эти пары, проигнорировав различие полов, и построить одну надежную модель по большой выборке объемом n1+ n2 ?
По методу Чоу строятся две линейные регрессионные модели с коэффициентами-векторами b‘ и b,, . Нулевая гипотеза Но: b‘ = b,, и D(e‘)=D(e,, )=s2, где e‘ и e,, - вектора-возмущения двух регрессий. Если Но верна, то эти две регрессионные модели схожи и объединяются в одну, т. е. строится единая модель по паре выборок объемом n1+n2 .
Нулевая гипотеза Но отвергается с уровнем значимости a, если выполняется неравенство - критерий Чоу:
|
|
|
 ,
| (4. 2) |
где å - оператор суммирования по i от 1 до n (по ошибкам объединенной регрессии), å ' - оператор суммирования по i от 1 до n1, å '' - оператор суммирования по i от n1+1 до n.
4. 4. Нелинейные регрессионные модели: классификация
и примеры
Вопрос нелинейности регрессионной модели не решается однозначно. Существует довольно сложная классификация нелинейных моделей (подробно см. работу [6, с. 124] и табл. 4. 2).
Таблица 4. 2
|
|
|
