 |
Численное интегрирование обыкновенных дифференциальных уравнений первого порядка
|
|
|
|
Постановка задачи
Многие практические задачи при их математическом моделировании сводятся к решению обыкновенных дифференциальных уравнений, т. е. к уравнениям, в которые входят независимая переменная, искомая функция и ее производные. В данной лабораторной работе рассматриваются численные методы поиска решения  для дифференциального уравнения первого порядка
для дифференциального уравнения первого порядка
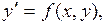 (4.1)
(4.1)
которое удовлетворяет начальному условию
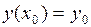 . (4.2)
. (4.2)
Известно [1]–[3], что для существования и единственности решения этой задачи(задача Коши) достаточно, чтобы функция  и ее частная производная
и ее частная производная  были непрерывны в некоторой области плоскости
были непрерывны в некоторой области плоскости  , содержащей окрестность точки
, содержащей окрестность точки  . В то же время аналитическое решение задачи Коши можно найти только в отдельных, наиболее простых случаях, изучаемых в курсе высшей математики [1]. В остальных случаях решение ищется приближенными методами.
. В то же время аналитическое решение задачи Коши можно найти только в отдельных, наиболее простых случаях, изучаемых в курсе высшей математики [1]. В остальных случаях решение ищется приближенными методами.
Все приближенные методы в зависимости от формы, в которой они представляют решение, можно условно разделить на следующие группы: аналитические (дают приближение 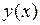 аналитическим выражением), графические (дают приближение
аналитическим выражением), графические (дают приближение 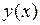 графиком) и численные (дают приближение
графиком) и численные (дают приближение 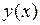 с помощью таблицы). В данной лабораторной работе рассматриваются лишь два из большого числа численных методов решения задачи Коши: метод Эйлера и метод Рунге-Кутта [1]–[3]. При этом решение
с помощью таблицы). В данной лабораторной работе рассматриваются лишь два из большого числа численных методов решения задачи Коши: метод Эйлера и метод Рунге-Кутта [1]–[3]. При этом решение  находится в виде таблицы своих значений:
находится в виде таблицы своих значений:  соответственно для значений аргумента:
соответственно для значений аргумента: 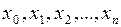 .
.
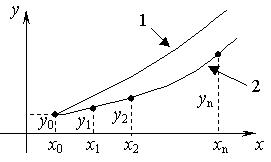
Рис. 4.1. Интегральная кривая y = y (x) (кривая 1) и
график приближенного решения задачи Коши (кривая 2)
Если соединить найденные в процессе решения точки  , гладкой кривой, то получим график приближенного решения задачи Коши (рис. 4.1). Этот график по мере удаления от начальной точки
, гладкой кривой, то получим график приближенного решения задачи Коши (рис. 4.1). Этот график по мере удаления от начальной точки  все более и более будет отклоняться от графика точного решения (интегральная кривая). Степень отклонения приближенного решения от точного характеризует точность численного метода.
все более и более будет отклоняться от графика точного решения (интегральная кривая). Степень отклонения приближенного решения от точного характеризует точность численного метода.
|
|
|
Метод Эйлера
Метод Эйлера состоит в следующем. Отрезок  , на котором ищется приближенное решение, делится точками
, на котором ищется приближенное решение, делится точками

на n равных частей, где 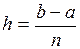 – шаг интегрирования дифференциального уравнения. Зная значение
– шаг интегрирования дифференциального уравнения. Зная значение  решения
решения  в точке
в точке 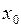 , можно найти приближенно
, можно найти приближенно  в точках
в точках  по следующей рекуррентной формуле:
по следующей рекуррентной формуле:
 (4.3)
(4.3)
Геометрически в методе Эйлера искомую интегральную кривую на интервале  заменяем отрезком касательной к этой интегральной кривой в точке
заменяем отрезком касательной к этой интегральной кривой в точке  (рис. 4.2). Уравнение касательной имеет вид
(рис. 4.2). Уравнение касательной имеет вид

где  . Поэтому ордината касательной в точке
. Поэтому ордината касательной в точке 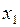 равна
равна  , т. е. получили формулу (4.3) для случая
, т. е. получили формулу (4.3) для случая  . Далее строим касательную в точке
. Далее строим касательную в точке  к интегральной кривой 2, которая уже не совпадает с искомой. Находим ординату
к интегральной кривой 2, которая уже не совпадает с искомой. Находим ординату  касательной в точке
касательной в точке 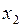 , получаем формулу (4.3) уже при
, получаем формулу (4.3) уже при  . И так до тех пор, пока не достигнем конца отрезка b (рис. 4.3).
. И так до тех пор, пока не достигнем конца отрезка b (рис. 4.3).

Рис. 4.2. Графическая иллюстрация метода Эйлера
1 – искомая интегральная кривая, 2,3 – другие интегральные кривые

Рис. 4.3. Графическая иллюстрация метода Эйлера
1 – ломаная Эйлера, 2 – искомая интегральная кривая
Для оценки локальной погрешности метода Эйлера в точке  используется неравенство [1]–[3]
используется неравенство [1]–[3]
 (4.4)
(4.4)
где 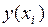 – точное значение решения задачи Коши в точке
– точное значение решения задачи Коши в точке  , а
, а  – приближенные значения решения, вычисленные по формуле (4.3) с шагами
– приближенные значения решения, вычисленные по формуле (4.3) с шагами  и
и  соответственно. Из неравенства (4.4) следует, что для достижения необходимой точности
соответственно. Из неравенства (4.4) следует, что для достижения необходимой точности  нужно просчитать значение
нужно просчитать значение  по формуле (4.3) с шагом
по формуле (4.3) с шагом  , а затем, уменьшив шаг вдвое, снова повторить расчеты. Если при этом окажется, что для всех
, а затем, уменьшив шаг вдвое, снова повторить расчеты. Если при этом окажется, что для всех  выполняется неравенство:
выполняется неравенство: 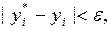 то на шаге
то на шаге  достигнута необходимая точность.
достигнута необходимая точность.
Метод Рунге-Кутта
Метод Эйлера прост в реализации, но обладает сравнительно небольшой точностью. Поэтому для решения задачи Коши с повышенной точностью обычно используют метод Рунге-Кутта [1]–[3].
|
|
|
Как и прежде, разбиваем отрезок интегрирования  на n равных частей. Зная значения
на n равных частей. Зная значения  – решение задачи Коши в точке
– решение задачи Коши в точке  , будем искать значение решения в точке
, будем искать значение решения в точке  по следующей формуле Рунге-Кутта:
по следующей формуле Рунге-Кутта:
 (4.5)
(4.5)
где
 (4.6)
(4.6)
Вычисления по формулам (4.5), (4.6) выполняются в следующем порядке. Для начальной точки  , где
, где  , вычисляют
, вычисляют  , затем последовательно
, затем последовательно  и
и  . После этого все значения подставляются в формулу (4.5)
. После этого все значения подставляются в формулу (4.5)  и находится
и находится  при
при  . Далее процесс продолжается аналогично до конца отрезка
. Далее процесс продолжается аналогично до конца отрезка  .
.
Для оценки локальной погрешности метода Рунге-Кутта используется уже неравенство [2], [3]:
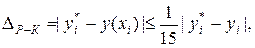 (4.7)
(4.7)
где  имеют тот же смысл, что и в неравенстве (4.4).
имеют тот же смысл, что и в неравенстве (4.4).
Выбор шага интегрирования
Точность методов Эйлера и Рунге-Кутта существенно зависит от величины шага интегрирования h. Можно доказать [2], [3], что погрешность метода Эйлера имеет порядок h, а метода Рунге-Кутта – порядок  . Т. е. для достижения одной и той же точности в методе Эйлера нужно выбрать гораздо меньший шаг интегрирования, чем в методе Рунге-Кутта.
. Т. е. для достижения одной и той же точности в методе Эйлера нужно выбрать гораздо меньший шаг интегрирования, чем в методе Рунге-Кутта.
Рассмотрим подробнее процедуру выбора и уточнения шага интегрирования на примере метода Рунге-Кутта. Пусть  – заданная точность решения задачи Коши. Поскольку
– заданная точность решения задачи Коши. Поскольку 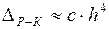 (где c = const), то начальное значение
(где c = const), то начальное значение  можно выбрать из неравенства
можно выбрать из неравенства
 (4.8)
(4.8)
При этом, чтобы попасть после n шагов интегрирования из точки a в точку b, необходимо одновременное выполнение условия:
 (целое число). (4.9)
(целое число). (4.9)
Кроме того, для подсчета погрешности метода Рунге-Кутта по формуле (4.7), нужно будет сделать просчет по формулам (4.5), (4.6) с шагом 2 h. Поэтому необходимо также, чтобы отношение 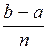 было четным.
было четным.
После выбора начального значения шага 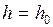 проводится его уточнение. Для этого из точки
проводится его уточнение. Для этого из точки  просчет по формулам (4.5), (4.6) выполняется дважды сначала с шагом h, а затем из той же точки с шагом 2 h. При этом получаются два значения решения задачи (
просчет по формулам (4.5), (4.6) выполняется дважды сначала с шагом h, а затем из той же точки с шагом 2 h. При этом получаются два значения решения задачи ( и
и 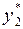 ) в одной и той же точке
) в одной и той же точке  . Если
. Если 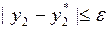 , то
, то  можно выбрать в качестве шага интегрирования, иначе необходимо уменьшить h в два раза и повторить процедуру проверки.
можно выбрать в качестве шага интегрирования, иначе необходимо уменьшить h в два раза и повторить процедуру проверки.
|
|
|


