 |
Создание декартовых графиков на плоскости
|
|
|
|
Нажмите клавишу ‘Shift’+‘2’ или введите с помощью мыши из всплывающего меню декартов график (View 
Toolbars Graph или Вид Панели инструментов График). В открывшемся поле графика (рис. 6.1) поместите в поле ввода 1 функцию или выражение, которое будет отображаться графически, а в поле ввода 2 непрерывную или дискретную переменную по которой строится график.
Рис. 6.1. Инициализация графика функции
Затем нажмите клавишу F9, чтобы построить график. По умолчанию, если функция определена, график будет построен на отрезке 
.
Например, необходимо ввести функцию 
и построить график этой функции на интервале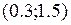 
.
Для этого определяем функцию 
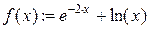
и в поле ввода 5 и 6 (рис. 6.2) помещаем начальное и конечное значение интервала 0.3 и 1.5 соответственно. В поле 3 и 4 показываются максимальное и минимальное значение функции на этом интервале.
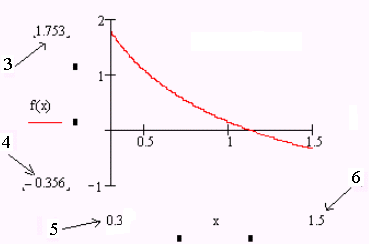
Рис. 6.2. Построение графика функции на отрезке
Чтобы на одном графике изобразить несколько функций, необходимо в поле ввода 1 (рис. 6.1) через запятую перечислить функции или выражения, которые будут отображаться графически, а в поле ввода 2 (рис. 6.1) через запятую соответствующие непрерывные или дискретные переменные (если переменные совпадают, то достаточно указать только одну переменную). Например, на рис. 6.3 построены графики функци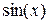й 
и 
.
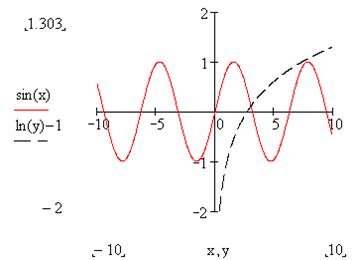
Рис. 6.3. Построение нескольких графиков
Если два раза щелкнуть мышью в поле графика, тогда во всплывающем окне «Formatting Currently Selected X-Y Plot» можно установить параметры отображения осей и линий графика. В первой закладке «X-Y Axes» («Оси X-Y») можно выбрать вид координатных осей, наложить сеть и установить ее размер, откорректировать масштаб. Во второй закладке «Traces» («След») можно установить параметры всех отображаемых линий (trace 1, trace2 и т. д.): наименование, цвет, толщину, тип (непрерывный, пунктир или точками для дискретных функций). В третьей закладке «Labels» («Метки») можно ввести названия графика и координатных осей.
|
|
|
Программные блоки
Для решения многих задач в системе Mathcad используются программные блоки. В начале любого блока обязательно должно присутствовать служебное слово Given, далее идет тело блока и в конце стандартная функция, закрывающая блок. В процессе программирования лабораторных работ были использованы четыре програмных блока.
В файле Lab1.mcd, в качестве дополнительной информации, показан способ получения общих решений систем линейных алгебраических уравнений и частных решений нелинейных систем с помощью программного блока «Given – Find». Например,
.
Здесь телом блока является система уравнений, а с помощью функции Find (x,y,….) получаем искомое решение, где x, y,... есть скалярные переменные, значения которых ищутся в блоке решения уравнений.
В файлах Lab2.mcd и Lab3.mcd для нахождения максимального и минимального значений функции в некоторой области использованы програмные блоки «Given – Maximize» и «Given – Minimize» соответственно. Например, для функции одной переменной 
найдем минимальное и максимальное значения функции на отрезке. Для этого найдем точки, в которых функция принимает эти значения
где до начала блока обязательно должны быть заданы функция и начальная точка 
. Тогда, получаем
.
Здесь телом блока является система ограничений, описывающая заданную область, а с помощью функций maximize (f, x, y,…) и minimize (f, x, y,…) получаем значения переменных x, y,…, при которых функция принимает максимальное и минимальное значения.
В файле Lab4.mcd для нахождения решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка, разрешенных относительно производной, используется программный блок «Given – Odesolve». Например,
|
|
|
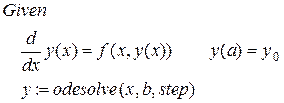
где 
– некоторая заданная функция, 
– заданное значение функции в точке 
, x – переменная интегрирования, a – начальная точка интегрирования, b – конечная точка интегрирования, [ step ] – шаг интегрирования (по умолчанию равен 0.1). Здесь телом блока является задача Коши, т. е. дифференциальное уравнение и начальное условие, а с помощью функции odesolve (x, b,[ step ]) получаем искомое решение y (x).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пискунов, Н. С. Дифференциальное и интегральное исчисления для втузов // Н. С. Пискунов. – М.: Наука, 1985. (Т.1.– 456 с., Т.2.– 576 с.)
2. Демидович, Б. П. Основы вычислительной математики // Б. П. Демидович, И. А. Марон. – М.: Наука, 1970.– 664 с.
3. Волков, Е. А. Численные методы // Е. А. Волков. – М.: Наука, 1987. – 354 с.
4. Вентцель, Е. С. Теория вероятностей // Е. С. Вентцель. – М.: Наука, 1964. – 576 с.
5. Лабораторные работы по высшей математике в классе КУВТ-86: методические указания // сост. В. В. Селиванов. – Ульяновск: УлГТУ, 1993. – 40 с.
6. Численное решение систем линейных алгебраических уравнений методом Гаусса: методические указания к выполнению лабораторной работы // сост. П. К. Маценко, Г. Д. Павленко, М. Е. Чумакин. – Ульяновск: УлГТУ, 1998. – 16 с.
7. Решение систем линейных алгебраических уравнений: методические указания к выполнению лабораторной работы // сост. Ш. Т. Ишмухаметов, М. Е. Чумакин. – Ульяновск: УлПИ, 1991. – 16 с.
8. Вычисление действительных корней алгебраических и трансцендентных уравнений с одним неизвестным: методические указания к выполнению лабораторной работы // сост. Н. Я. Горячева, П. К. Маценко. – Ульяновск: УлГТУ, 1997. – 24 с.
9. Вычисление действительных корней алгебраических и трансцендентных уравнений с одним неизвестным: методические указания к выполнению лабораторной работы // сост. Н. Я. Горячева, А. В. Жарков, П. К. Маценко. – Ульяновск: УлПИ, 1991. – 24 с.
10. Определенный интеграл: методические указания к лабораторной работе // сост. П. А. Вельмисов, П. К. Маценко. – Ульяновск: УлГТУ, 1998. – 16 с.
11. Определенный интеграл: методические указания к выполнению лабораторной работы // сост. П. А. Вельмисов, Д. Р. Воденин, А. В. Егоров. – Ульяновск: УлПИ, 1991. – 16 с.
12. Численные методы решения дифференциальных уравнений 1 порядка: методические указания к выполнению лабораторной работы // сост. Д. Р. Воденин, П. К. Маценко. – Ульяновск: УлПИ, 1991. – 12 с.
|
|
|
13. Аппроксимация функции на основании экспериментальных данных по методу наименьших квадратов: методические указания к выполнению лабораторной работы // сост. И. В. Коноплева, Л. А. Крашенинникова. – Ульяновск: УлПИ, 1991. – 16 с.
|
|
|
