 |
66. Эффективный набор портфелей.
|
|
|
|
66. Эффективный набор портфелей.
Эффективный набор портфелей Марковица - набор эффективных портфелей, графически обозначаемый как эффективная граница Марковица.
Если объединить в портфель некоторое число активов, корреляция доходности которых лежит в диапазоне от -1 до +1, то, в зависимости от их удельных весов, можно построить множество портфелей с различными параметрами риска и доходности, которые расположены в рамках фигуры ABCDE, как показано на рис. 46.
Рациональный инвестор будет стремиться минимизировать свой риск и увеличить доходность. Поэтому всем возможным портфелям, представленным на рис. 46, вкладчик предпочтет только те, которые расположены на отрезке ВС, поскольку они являются доминирующими по отношению к портфелям с тем же уровнем риска или с той же доходностью. Набор портфелей на отрезке ВС называют эффективным набором. Эффективный набор портфелей — это набор, состоящий из доминирующих портфелей. Набор портфелей на участке ВС называют еще эффективной границей. Она открыта Г. Марковцем в 50-х гг. Чтобы определить данную границу, необходимо рассчитать соответствующие удельные веса, входящих в портфель активов, при которых минимизируется значение стандартного отклонения для каждого данного уровня доходности, т. е. решить уравнение:
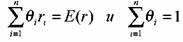, с помощью компьютерной программы необходимо для каждого значения ожидаемой доходности портфеля определить наименьший риск портфеля. Данный метод называется методам Марковца. Неудобство его состоит в том, что при определения эффективной границы для портфеля, включающего много активов, не-обходимо произвести большое количество вычислений. Если портфель состоит из п активов, то следует определить п ожидаемых
|
|
|
доходностей и стандартных отклонений иковариаций.
границы следует рас-
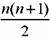отдельных показателей ожидаемой доходности, дисперсий и ковариаций. Так, если мы определяем эффективную границу для портфеля из 5 активов, то необходимо получить 20 исходных данных, для 10 активов - уже 65, для 20 активов - 230, а для 30 активов - 495 данных и т. д. Таким образом, большое количество вычислений делает модель Марковца не очень удобной для решения задачи определения эффективной границы. Эта проблема в более простой форме решена в моделе У. Шарпа, которая будет представлена ниже.
48. Модель САРМ и её модификации.
Теория Марковица стала огромным шагом на пути создания модели оценки стоимости активов Capital Asset Pricing Model (CAPM). Модель оценки стоимости активов описывает взаимосвязь между риском и ожидаемой доходностью активов. Взаимосвязь риска с доходностью согласно модели оценки долгосрочных активов описывается следующим образом:
Д = Дб/р + β × (Др - Дб/р),
где Д - ожидаемая норма доходности;
Дб/р - безрисковая ставка (доход);
Др - доходность рынка в целом;
β - коэффициент бета.
Основная идея CAPM заключается в том, что инвесторы должны получать 2 вида компенсации: за время (временная стоимость денег) и за риск. Стоимость денег во времени представлена безрисковой ставкой и является компенсацию инвестору за то, что он размещает денежные средства в какие-либо инвестиции на определенный период времени.
Коэффициент бета определяется по формуле:
β = Соrх × δ х / δ
или β = Covx / δ 2,
где Соrх - корреляция между доходностью ценной бумаги х и средним уровнем доходности ценных бумаг на рынке;
Covx - ковариация между доходностью ценной бумаги х и средним уровнем доходности ценных бумаг на рынке;
δ х - стандартное отклонение доходности по конкретной ценной бумаге;
|
|
|
δ - стандартное отклонение доходности по рынку ценных бумаг в целом.
Уровень риска отдельных ценных бумаг определяется на основании таких значений:
β = 1 - средний уровень риска;
β > 1 - высокий уровень риска;
β < 1 - низкий уровень риска.
Акции с большой бетой (β > 1) называют агрессивными, с низкой бетой (β < 1) - защитными.
|
|
|
