 |
Квинтили делят ранжированный ряд на пять равных частей.
|
|
|
|
Квинтили делят ранжированный ряд на пять равных частей.
Децили (D) делят ранжированный ряд на десять равных частей: первым децилем (D1) является значение признака, которое не превышает 10% единиц совокупности, вторым (D2) – 20%, третьим (D3) – 30% и т. д. При этом пятый дециль (D5) совпадает с медианой и вторым квартилем (Q2)
Перцентили делят ранжированный ряд на сто равных частей.
Абсолютные и средние показатели вариации, характеризующие колеблемость значений варьирующего признака, позволяют, измерить степень связи и взаимосвязи, оценить степень однородности совокупности, типичность и устойчивость средней, определить величину возможной погрешности выборочного наблюдения.
Изучая эту тему необходимо уяснить сущность, назначение и способы вычисления каждого показателя вариации.
Размах вариации показывает различие крайних значений признака:
Среднее линейное отклонение это средняя арифметическая из отклонений индивидуальных значений признака от средней арифметической, рассчитанная без учета знаков этих отклонений.
Рассчитывается по формулам: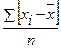 
невзвешенная, 
взвешенная
где 
значение осредняемого признака, 
варианта.
Дисперсия это средний квадрат отклонений вариантов признака от их средней величины:
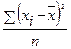, невзвешенная 
, взвешенная
где 
значение осредняемого признака, варианта
 |
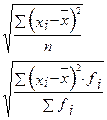Среднее квадратическое отклонение- это корень квадратный из дисперсии.
Показатели относительного рассеивания позволяют сравнивать характер рассеивания в различных совокупностях.
Коэффициент осцилляции отражает относительную колеблемость крайних значений вокруг средней: 
, где R – размах вариации,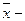 
среднее значение.
|
|
|
Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений вокруг средней величины: 
, где 
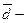среднее линейное отклонение, 
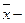среднее значение.
Коэффициент вариации характеризует меру колеблемости изучаемых признаков, степень однородности совокупности, типичность, устойчивость средней: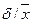 
, где 
среднее квадратическое отклонение, 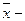среднее значение.
Для определения влияния отдельных факторов на колеблемость индивидуальных значений признака осуществляют группировку по однородным факторам и рассчитываю три показателя колеблемости.
Общую дисперсию, характеризующую вариацию признака, зависящую от одновременного влияния всех факторов в данной совокупности: 
, где 
– общая средняя по всей совокупности
Межгрупповую дисперсию, характеризующую влияние на колеблемость изучаемого признака лишь под влиянием факторного (группировочного) признака: 
,
где 
общая средняя (во всей совокупности), 
групповая средняя (внутри группы),
частота по группам
Среднюю внутригрупповую дисперсию, характеризующую влияние на колеблемость изучаемого признака в внутри каждой группы всех прочих случайных факторов (кроме группировочного признака):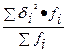 
, где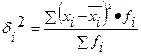 
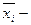групповая средняя, 
отдельные значения признака, частота
Тема 6 Методы выборочного наблюдения
Тема Методы выборочного наблюдения тесно взаимосвязана с другими темами: Статистическое наблюдение, Обобщающие статистические показатели, Средние величины и показатели вариации, кроме того основывается на фундаментальных положениях теории вероятности и математической статистики.
Основными задачами темы являются:
· определение способа формирования выборки (собственно- случайная, механическая, типическая, серийная, комбинированная)
· расчет ошибок выборки
|
|
|
· построение доверительных интервалов выборочных характеристик
· расчет необходимого объема выборки.
Расчет ошибок выборки позволяет оценить репрезентативность (представительность) выборочной совокупности. Различают среднюю, относительную и предельную выборки.
Средняя ошибка выборки при повторном наблюдении рассчитывается по формуле: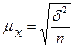 
Средняя ошибка выборки при бесповторном наблюдении рассчитывается по формуле:
Дисперсия количественного признака в выборке определяется по формулам:
- невзвешенной,
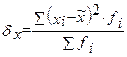- взвешенной.
Средняя ошибка выборки для показателя доли альтернативного признака при повторном отборе определяется по формуле: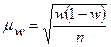 
Средняя ошибка выборки для показателя доли альтернативного признака при бесповторном отборе определяется по формуле: 
Величина 
в статистике называется предельной ошибкой выборки.
Расчет предельной ошибки позволяет определить возможные пределы нахождения характеристик генеральной совокупности (генеральной средней, генеральной доли) с заданной степенью доверительной вероятности.
Генеральная средняя определяется по формуле: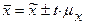 
,
где 
- выборочная средняя;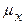 
- средняя ошибка выборки, 
- коэффициент доверия.
Доля альтернативного признака в генеральной совокупности определяется по формуле: 
, где 
- выборочная доля альтернативного признака, 
- средняя ошибка выборки для показателя доли альтернативного признака.
Коэффициент доверия определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного наблюдения
| Коэффициент доверия | 0, 1 | 0, 5 | 1, 0 | 1, 5 | 2, 0 | 2, 5 | 3, 0 | 4, 0 |
| Вероятность | 0, 0797 | 0, 3829 | 0, 6827 | 0, 8664 | 0, 9545 | 0, 9876 | 0, 9973 | 0, 9999 |
|
|
|
