 |
Вычислительные приемы для многозначных чисел
|
|
|
|
Способы устных вычислений
Устные приемы сложения и вычитания многозначных чисел изучаются в 4 классе четырехлетней начальной школы в следующем порядке:
1. Нумерационные случаи
а) Случаи вида:
99 999 + 1 345 000 - 1 560 999 + 1
560 000 - 1 399 999 + 1 40 000 - 1
При выполнении вычислений данного вида ссылаются на принцип построения натурального ряда чисел: добавление к числу единицы дает число, следующее по счету; вычитание единицы дает число, предшествующее по счету.
Например: 399 999 + 1 — добавляя к числу 1, получаем число следующее. Следующее за числом 399 999 число 400 000, значит 399 999 + 1 =400 000.
б) Случаи вида:
30 000 + 1 000 650 999 - 900 600 000 + 5
60 345 - 5 345 000 - 45 000 800 700 + 1 000
При выполнении вычислений данного вида ребенок должен хорошо знать принцип поразрядного строения чисел в десятичной системе счисления.
650 999 - 900 - 650 099

50 000 900 90
2. Сложение и вычитание целых тысяч
Сложение и вычитание вида 32 000 + 2 000, 690 000 - 50 000 является первым вычислительным приемом, с которого начинается формирование устных вычислений в объеме многозначных чисел.
Для освоения этого приема ребенок должен хорошо представлять разрядный состав многозначного числа. Рассматривая 32 000 как 32 тыс. и 2 000 как 2 тыс., прием 32 000 + 2 000 вычисляется, как 32 тыс. + 2 тыс. Ответ 34 тыс. затем рассматривается, как 34 000 и записывается результат вычислений. Таким образом, действия целыми тысячами рассматриваются как действия разрядными единицами, вычисления в этом случае сводятся к табличным вычислениям в пределах 10, 20 пли 100.
3. Сложение и вычитание целых тысяч на основе правил арифметических действий
Учебник математики для 4 класса практически не предлагает вычислений соответствующего вида, однако учителя часто используют их на устном счете.
|
|
|
К этим случаям относятся вычисления вида: 70 200 + 400, 600 100 - 99, 3 008 + 351,425 100 - 24 100 и т. п.
При вычислениях используется знание десятичного состава многозначных чисел и понимание того, что во всех случаях действия затрагивают только часть первого числа (первое число может рассматриваться как сумма). Таким образом действия могут выполняться только с частью первого числа.
Например:
Вычисляя сумму 70 200 + 400, можно отдельно сложить 400 и 200, а затем их сумму прибавить к числу 70 000. Фактически используется правило прибавления числа к сумме.
При выполнении вычислений в случае 425 100 - 24 100 используется правило вычитания числа из суммы. 425 100 рассматривается, как сумма 400 000 и 25 100. Из одного из слагаемых вычитается 24 100 (25 100 - 24 100 = 1 000), и полученный результат складывается с первым слагаемым: 400 000 + 1 000 = 401 000.
В основе всех этих случаев лежит хорошее знание разрядного состава многозначных чисел и умение выполнять устные вычисления целыми разрядами.
Способы письменных вычислений (в столбик)
Письменные приемы сложения и вычитания являются основными вычислительными действиями при вычислениях в объеме многозначных чисел, поскольку вычисления в уме с многозначными числами представляют собой слишком сложную проблему для всех детей. Использование письменных алгоритмов вычислений в этих условиях является психологически и методически оправданным.
Усвоение детьми нумерации четырехзначных и многозначных чисел позволяет им осуществить перенос умения складывать и вычитать числа «столбиком» из области трехзначных чисел на область многозначных чисел.
При знакомстве с письменными приемами сложения и вычитания в объеме многозначных чисел проводится аналогия с алгоритмом письменного сложения и вычитания в пределах 1000:
1) Письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трехзначных чисел.
|
|
|
2) При записи столбиком, как и при сложении трехзначных чисел следует записывать разряд под соответствующим разрядом, и складывать сначала единицы, потом десятки, а потом сотни, потом тысячи и т. д. (справа налево).
Считается, что дети хорошо научены выполнять действия сложения и вычитания в столбик, поэтому в учебнике 4 класса не предусмотрено распределение случаев сложения и вычитания по уровням сложности.
Первыми рассматриваются различные случаи с переходами через разряд как при сложении так и при вычитании: 3 126 + 4 232; 25 346 - 13 407.
Затем рассматриваются случаи вычитания с нулями в уменьшаемом:
600 - 25; 1 000 - 124; 30 007 - 648.
Эти случаи являются наиболее сложными, поскольку требуют «заема» разрядных единиц не из соседних, а из далеко отстоящих разрядов. Эти случаи полезно сначала сопровождать подробной пояснительной записью на доске, чтобы дети понимали и видели, откуда появляются девятки в «пустых» разрядах.
Например:
30 007 Вычитаю единицы. Из 7 нельзя вычесть 8. 648 Пробую занять единицу в соседнем разряде.
В разряде десятков, сотен и тысяч нет разрядных единиц, поэтому «заем» возможно произвести только из разряда десятков тысяч: 30 тыс. - 1 тыс. = 29 тыс. Подписываем 29 над 30.
«Занятую» тысячу представляем в виде суммы 1 тыс. = 1000 = = 990 + 10.
Подписываем над разрядами сотен и десятков девятки, а из 10 единиц вычитаем 8, получаем 2 единицы. Но в разряде единиц было 7 единиц. Добавляем их к полученным 2 единицам и пишем в разряде единиц 9.
Вычитаем: 9 дес. - 4 дес. = 5 дес. Пишем 5 в разряде десятков. 9 сот. - 6 сот. = 3 сот. Пишем 3 в разряде сотен.
От десятков тысяч осталось 29 тыс. Пишем 9 в разряде тысяч, 2 — в разряде десятков тысяч.
При изучении сложения и вычитания многозначных чисел рекомендуется повторять и закреплять названия компонентов и результатов действий; свойства нахождения неизвестных компонентов действий при проверке результатов вычислений; рассматривать закономерности изменения суммы и разности при изменении одного из компонентов действий.
Многие дети используют калькуляторы как при выполнении вычислений с многозначными числами, так и при проверке результатов. В старших классах не возбраняется использовать калькуляторы при необходимости выполнить громоздкие вычисления (на уроках физики, химии, геометрии).
|
|
|
Чтобы стимулировать ребенка к использованию умения самостоятельно вычислять в столбик, следует предлагать задания, не позволяющие механического использования калькулятора для вычисления результата. Это различные задания на нахождение ошибки в записях или цифрах вычислений, на прикидку округленных результатов вычислений, на восстановление пропущенных цифр в компонентах действий, на выбор верных ответов из предложенных и т. п. Учителю следует помнить, что механический характер вычислительных действий при вычислениях с многозначными числами быстро приводит к утомлению детей, что провоцирует появление ошибок. Поэтому не стоит задавать подряд больше трех примеров на вычисления с многозначными числами.
Лекция 10. Умножение
1. Смысл действия умножения.
2. Табличное умножение.
3. Приемы запоминания таблицы умножения.
Смысл действия умножения
Действие умножения рассматривается как суммирование одинаковых слагаемых.
По определению умножение целых неотрицательных чисел (натуральных) — это действие, выполняющееся по следующим правилам:
а •b = a+ a+ a+ a+ a...+ а, при b > 1
b слагаемых
а •1 = а, при b = 1
а•0 = 0, при b = 0
Использование символики умножения позволяет сократить запись сложения одинаковых слагаемых.
Запись вида 2-4 = 8 подразумевает сокращение записи вида 2 + 2 + 2 + 2 = 8. Ее читают так: «по 2 взять 4 раза, получится 8»; или: «2 умножить на 4 получится 8».
Действие умножения во всех учебниках математики для начальных классов рассматривают ранее действия деления.
С теоретико-множественной точки зрения умножению соответствуют такие предметные действия с совокупностями (множествами, группами предметов) как объединение равных (равночисленных) совокупностей. Поэтому, прежде, чем знакомиться с символикой записи действий и вычислениями результатов действий, ребенок должен научиться моделировать на предметных совокупностях все эти ситуации, понимать (т. е. правильно представлять) их со слов учителя, уметь показывать руками как процесс, так и результат предметного действия, а затем характеризовать их словесно.
|
|
|
Виды заданий, которые предлагаются детям до знакомства с символикой действия умножения (в 1 и 2 классе):
1. Посчитай двойками (тройками, пятерками).
2. Нарисуй рисунок: «На трех тарелках по 2 апельсина». Сосчитай, сколько всего апельсинов.
3. Найди лишнюю запись:
2 + 2
2 + 2 + 2
2+2+2+2
2+3+2+2+2
Найди значение каждого выражения наиболее удобным способом.
4. Сделай запись выражения по рисунку:
Виды заданий, используемых для усвоения ребенком смысла умножения при знакомстве с этим действием:
а) На соотнесение рисунка и математической записи:
Рассмотри рисунок и объясни записи:
2 + 2 + 2 + 2 + 2 = 10и2.5 = 10 5 + 5= 10и5-2= 10

4 + 4 + 4 = 12 4-3=12
б) На нахождение суммы одинаковых слагаемых: Рассмотри рисунки и закончи записи:
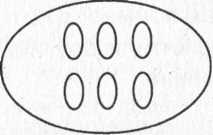
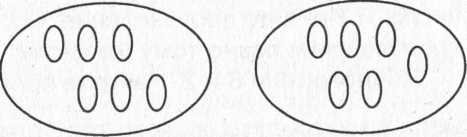
6+6+6=.
6-3 =.
в) На замену сложения умножением:
Замени, где возможно сложение умножением и вычисли результаты:
5+5+5+5 1+1+1+1+1 5+6+3
42 + 42 0 + 0+0 + 0 + 0 4 + 6 + 8
г) На понимание смысла определения действия умножения:
Рассмотри записи и объясни, какое число берется слагаемым и сколько раз берется слагаемым это число: 6-4 = 24 9-3 =...
6 + 6 + 6 + 6 = 24 9 + 9 + 9 =...
Выражение вида 3 • 5 называют произведением. Числа 3 и 5 в этой записи называют сомножителями (множителями).
Запись вида 3 • 5 = 15 называют равенством. Число 15 называют значением выражения. Поскольку число 15 в данном случае получено в результате умножения, его также часто называют произведением.
Например:
Найдите произведение чисел 4 и 6. (Произведение чисел 4 и 6 — это 24.)
Поскольку названия компонентов действия умножения вводятся по соглашению (детям сообщаются эти названия и их необходимо запомнить), педагог активно использует задания, требующие распознавания компонентов действий и употребления их названий в речи.
Например:
1. Среди данных выражений найдите такие, в которых первый множитель равен 3 (второй множитель равен 2 и т. д.):
2-2 7-3 6-2 1.6 3-5 3-2 7-3 3-4 3-1
2. Составьте произведение, в котором второй множитель равен 5. Найдите его значение.
3. Выберите примеры, в которых произведение равно 6. Подчеркните их красным цветом. Выберите примеры, в которых произведение равно 12. Подчеркните их синим цветом.
7-3 6-1 2-2 2-3 6-2 3-2 2-6
4. Как называют число 4 в выражении 5 • 4? Как называют число 5? Найдите произведение. Составьте пример, в котором произведение равно тому же числу, а множители другие.
5. Множители 8 и 2. Найдите произведение.
В третьем классе дети знакомятся с правилом взаимосвязи компонентов умножения, которое является основой для обучения нахождению неизвестных компонентов умножения при решении уравнений:
|
|
|
Если произведение разделить на один множитель, то получится другой множитель.
Например:
Решите уравнение 6 * х = 24. (В уравнении неизвестен множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. х= 24:6, х = 4.)
Однако, данное правило в учебнике математики 3 класса не является обобщением представлений ребенка о способах проверки действия умножения. Правило проверки результатов умножения рассматривается в учебнике намного позже — после знакомства с вне-табличным умножением и делением (знакомства с умножением и делением двузначных чисел на однозначные, не входящим в таблицу умножения и деления). Это объясняется тем, что правило взаимосвязи компонентов умножения является основой составления таблицы деления. Поскольку предполагается, что табличные случаи умножения ребенок к этому времени знает наизусть, то нет необходимости в проверке результатов. Есть только необходимость быстро восстанавливать (вспоминать) нужное третье число по двум данным.
Например:
Вычисли
9-2 =... 5-4 =... 1*7 =...
18:2 =... 20:4 =... 7:7 =...
При выполнении устного внетабличного умножения, требующего применения достаточно сложного алгоритма, необходима проверка, поскольку многие дети часто ошибаются в этих случаях.
Правило проверки действия умножения:
1) Произведение делят на множитель.
2) Сравнивают полученный результат с другим множителем. Если эти числа равны, умножение выполнено верно.
Например: 18 • 4 = 72. Проверка: 1) 72: 4 = 18; 2) 18 = 18.
Табличное умножение
Изучение таблицы умножения является центральной задачей обучения математике во 2 и 3 классе.
К табличному умножению относят случаи умножения однозначных натуральных чисел на однозначные натуральные числа, результаты которых находят на основе конкретного смысла действия умножения (находят суммы одинаковых слагаемых).
Результаты табличного умножения в соответствии с программными требованиями к знаниям, умениям и навыкам дети должны знать наизусть. Умножение с числом нуль, умножение с числами 1 и 10 относят к особым случаям.
Первые приемы составления таблиц умножения связаны со смыслом действия умножения (см. предыдущий пункт). Результаты этих таблиц получают последовательным сложением одинаковых слагаемых.
Например:
| Умножение числа 2 | ||||
| Вычисли и запомни: | ||||
| 2+2 | •2 | |||
| 2 + 2 + 2 | •3 | |||
| 2+2+2+2 | •4 | |||
| 2+2+2+2+2 | •5 |
Расположенный рядом рисунок помогает ребенку получить результат пересчетом фигурок. При небольших значениях множителей прием сосчитывания для получения табличного значения произведения вполне приемлем, и учитель им часто пользуется при получении результатов таблиц значений умножения чисел 2, 3, 4. Приведенный пример показывает, что этот прием удобен лишь при небольших значениях второго множителя.
При значении второго множителя больше 5, удобнее использовать для получения результатов табличных значений другой прием: прием прибавления к предыдущему результату. Например:
Вычисли и запомни: 2-6 = 2.5 + 2 =... 2-7 = 2.6 + 2 =... 2-8 = 2.7 + 2 2.9 = 2-8 + 2 =...
В учебнике математики для 2 класса этот прием дан более пространно, и поэтому не всегда правильно понимается с точки зрения техники выполнения:
2+2+2+2+2+2 2-6
2 + 2 + 2 + 2 + 2 + 2 + 2 2-7ит.п.
Аналогичным образом составляется таблица значений умножения числа 3.
Следующим приемом, на основе которого составляются таблицы значений умножения чисел, является прием перестановки множителей.
Этот прием фактически является первым математическим законом относительно действия умножения в начальной школе:
От перестановки множителей произведение не меняется.
Способ знакомства детей с этим правилом (законом) обусловлен ранее введенным смыслом действия умножения. Используя предметные модели множеств, дети сосчитывают результаты группировки их элементов разными способами, убеждаясь, что результаты не меняются от изменения способов группировки.
Например:
2*3 = 6
3*2=6
Счет элементов рисунка (множества) парами по горизонтали совпадает со счетом элементов тройками по вертикали. Рассмотрение нескольких вариантов подобных случаев дает учителю основание произвести индуктивное обобщение (т. е. обобщение нескольких частных случаев в обобщенном правиле) о том, что перестановка множителей не меняет значение произведения.
На основе этого правила, используемого как прием счета, составляется таблица умножения на 2.
Например:
Используя таблицу умножения числа 2, вычисли и запомни таблицу умножения на 2:
3 = 6
4 = 8 5= 10
6 = 12
7 = 14
8 = 16 9= 18
2 = 2 = 2 = 2 = 2 = 2 = 2 =
На основе этого же приема составляется таблица умножения на 3:
3-4 = 12 3-7 = 21 4-3 =... 7-3=...
3-5= 15 3-8 = 24 5-3 =... 8-3 =...
3-6 = 18 3-9 = 27 6-3=... 9-3 =...
Составление двух первых таблиц распределяется на два урока, что соответственно увеличивает время, отведенное на их заучивание. Каждая из двух последних таблиц составляется на одном уроке, поскольку предполагается, что дети, зная исходную таблицу, не должны отдельно заучивать результаты таблиц, полученных с помощью перестановки множителей. На самом деле, многие дети учат каждую таблицу отдельно, поскольку недостаточный уровень развития гибкости мышления не позволяет им легко перестроить модель заученной схемы табличного случая в обратном порядке. При вычислении случаев вида 9 • 2 или 8 • 3 дети снова возвращаются к приему последовательного сложения, что естественно требует времени для получения результата. Такая ситуация порождается скорее всего тем, что для значительного числа детей такое разнесение во времени взаимосвязанных случаев умножения (тех, что связаны правилом перестановки множителей) не позволяет сформироваться ассоциативной цепочке, ориентированной именно на взаимосвязь. Та же ситуация прослеживалась у ряда детей при применении свойства перестановки слагаемых для составления таблиц сложения: запомнив случай 3 + 5, такой ребенок учит отдельно случай 5 + 3, поскольку требование выучить этот случай поступает от учителя через 16 уроков после требования заучить первый, и при этом в промежутке заучивалась таблица вида □ + 4, □ - 4. Иными словами, отсрочка в образовании ассоциативной связи, ориентированной на взаимосвязь этих случаев, оказалась для ребенка слишком большой, что помешало образованию такой связи. Поэтому каждый случай из фактически взаимосвязанной пары учится ребенком наизусть отдельно.
При составлении таблицы умножения числа 5 в 3 классе, только первое произведение получают путем сложения одинаковых слагаемых: 5-5 = 5 + 5 + 5 + 5 + 5 = 25. Остальные случаи получают приемом прибавления пяти к предыдущему результату:
5-6 = 5- 5 + 5 = 30 5-7 = 5-6 + 5 = 35 5-8 = 5-7 + 5 = 40 5-9 = 5- 8 + 5 = 45
Одновременно с этой таблицей составляется и взаимосвязанная с ней таблица умножения на 5: 6 • 5; 7 • 5; 8 • 5; 9 • 5.
Таблица умножения числа 6 содержит четыре случая: 6 • 6; 6 • 7; 6-8; 6-9.
Таблица умножения на 6 содержит три случая: 7 • 6; 8 • 6; 9 • 6.
Таблица умножения числа 7 содержит три случая: 7 • 7; 7 • 8; 7 • 9.
Таблица умножения на 7 содержит два случая: 8 • 7; 9 • 7.
Таблица умножения числа 8 содержит два случая: 8 • 8; 8 • 9.
Таблица умножения на 8 содержит один случай: 9 • 8.
Таблица умножения числа 9 содержит, только один случай: 9 • 9.
Теоретический подход к подобному построению системы изучения табличного умножения предполагает, что именно в таком соответствии ребенок и будет запоминать случаи табличного умножения.
Наибольшее количество случаев содержит наиболее легкая для запоминания таблица умножения числа 2, а наиболее трудная для запоминания таблица умножения числа 9 содержит всего один случай. Реально, рассматривая каждую новую «порцию» таблицы умножения, учитель обычно восстанавливает весь объем каждой таблицы (все случаи). Даже при условии, что учитель обращает внимание детей на то, что новым случаем на данном уроке является, например, только случай 9 • 9, а 9 • 8, 9 • 7 и т. п. изучались на предыдущих уроках, большая часть детей воспринимает весь предложенный объем как материал для нового заучивания. Таким образом, фактически, для многих детей таблица умножения числа 9 является самой большой и сложной (а это действительно так, если иметь в виду перечень всех случаев, который к ней относится).
Большой объем материала, требующего заучивания наизусть, сложность в образовании ассоциативных связей при запоминании взаимосвязанных случаев, необходимость достижения всеми детьми прочного запоминания всех табличных случаев наизусть в установленные программой сроки — все это делает тему изучения табличного умножения в начальных классах одной из наиболее методически сложных. В связи с этим важными являются вопросы, связанные с приемами запоминания ребенком таблицы умножения.
|
|
|


