 |
Приемы запоминания таблицы умножения
|
|
|
|
1. Прием счета двойками, тройками, пятерками
Прием обучения ребенка счету двойками, тройками, пятерками применяется до знакомства с действием умножения. Методически целесообразно применять этот прием уже в первом классе. Обучение ребенка свободному счету двойками, тройками, пятерками является подготовительным приемом к знакомству с умножением и таблицей умножения. Технологически этот прием соответствует приему заучивания состава однозначных чисел до знакомства с табличным сложением в первом классе. При хорошем усвоении таких способов счета ребенку будет легко освоить таблицы умножения чисел 2, 3 и 5. Знание этого базового объема табличных случаев поможет ребенку при освоении более сложных случаев.
2. Прием последовательного сложения
Прием последовательного сложения одинаковых слагаемых является основным приемом получения результатов табличного умножения. Данный прием связан со смыслом действия умножения как сложения одинаковых слагаемых. Прием последовательного сложения продолжает оставаться достаточно удобным даже при вычислении табличных случаев умножения чисел 7, 8 и 9, при небольших значениях второго множителя.
Например: 6-7 = 6 + 6 + 6 + 6 + 6+.-6+ 6. Найти значение произведения чисел 6 и 7 таким способом достаточно сложно. Но для случаев 8 • 3 или 9 • 2 этот способ достаточно удобен.
3. Прием прибавления слагаемого к предыдущему результату (вычитания из предыдущего результата)
Данный прием является вторым основным приемом получения результатов табличного умножения. Используется в том случае, если ребенок смог выучить хотя бы несколько случаев из каждой таблицы. Это могут быть 3—4 первых самых легких случая, или 2—3 наиболее запоминающихся случая.
|
|
|
Так, приведенный выше случай 6 • 7 является одним из наиболее плохо запоминающихся случаев. В то же время случаи 6 • 6 и 6 • 8 наиболее легко запоминаются из этой таблицы. Запомнив результат 6 • 6 = 36, ребенок может использовать прием прибавления 6 к предыдущему результату для получения значения случая 6 • 7. Запомнив случай 6 • 8, ребенок использует прием вычитания 6 из его результата. Для осознанного применения этого приема необходимо хорошее понимание смысла действия умножения и смысла каждого множителя в записи действия умножения: чтобы получить 6 • 6 надо по 6 взять шесть раз, значит, чтобы получить 6 • 7 надо по 6 взять семь раз, т. е. 6 • 7 = 6 • 6 + 6 = 36 + 6 = 42 или 6 • 7 = = 6 • 8 - 6 = 48 - 6 = 42.
Кроме того, необходимо уметь выполнять сложение и вычитание в пределах 100 в уме.
4. Прием взаимосвязанной пары: 2 • 6 6-2 (перестановка множителей)
При хорошем понимании правила перестановки множителей ребенок заучивает в два раза меньше случаев табличного умножения, чем содержит полная таблица. Используя перестановку множителей, все остальные случаи можно получить из имеющихся.
5. Прием запоминания последовательности случаев с ориентиром на возрастание второго множителя
Этот прием активно реализован в традиционном учебнике по математике для 2 и 3 классов, где табличные случаи предлагаются ребенку на уроке «серией»:
3-2 3-3 3-4 3-5
Эту же «серию» учитель предлагает детям для заучивания к следующему уроку. На следующем уроке изучается новая «серия»: 3-6 3-7 3-8 3-9
Эта же «серия» предлагается детям для заучивания. В каждой серии задано последовательное увеличение второго множителя. Ребенок фиксирует серию как визуально, так и мнемонически (учит на память, глядя на запись). В результате может получиться парадоксальный результат: от начала до конца, т. е. подряд ребенок «серию» воспроизводит, а отдельные случаи вразбивку восстановить не может (выучил как стихи).
|
|
|
6. Прием «порции»
Этот прием активно реализован в учебнике математики для 2 и 3 классов автора Н.Б. Истоминой. Для заучивания ребенку предлагается «порция», состоящая из 2—3 случаев, но не по принципу возрастания второго множителя.
Например, «порция» состоит из трех случаев: 9 • 5; 9 • 6; 9 • 7. Первым для заучивания предлагается случай 9 • 6, а от него, используя прием 3, ребенок переходит к случаям 9 • 5 и 9 • 7.
В следующий раз «порция» снова содержит три случая 9 • 4; 9 • 3; 9 • 2. Здесь опорным случаем является случай 9 • 3.
7. Прием запоминающегося случая в качестве опорного
Например, 5 • 6 = 30, значит 5 • 7 = 30 + 5 = 35.
Прием является производным от приема 3. Используются легко запоминающиеся случаи: 6 • 5, 6 • 8, 5 • 4, 5 • 9, 7 • 7, 6 • 6, 5 • 5 и т. п. Применяя затем прием прибавления или вычитания первого множителя, ребенок получает нужные результаты.
8. Прием внешней опоры
В качестве опоры используется рисунок или прямоугольная таблица чисел.
Детям, которые обладают плохой механической памятью, можно на первых порах предложить использовать клетчатое поле тетради.
Обводя на клетчатом поле прямоугольник с заданным количеством клеток в сторонах, ребенок использует эту модель для контроля полученного результата или просто подсчитывает клетки как умеет.
Например:
4 * 5 = 20
Задание:
Найди результаты умножения и проверь себя по рисунку:
2*3 =6 3*2=6
2*4 = 4*2=
В качестве внешней опоры может также использоваться прямоугольная таблица чисел, позволяющая получить результаты умножения в пределах 100. Такая таблица часто помещается на последней обложке тетрадей в клетку:
8 • 7 - 7• 8 - 56
|
|
|
9. Прием запоминания таблицы «с конца»
Прием активно реализован в учебнике Н.Б. Истоминой. Он рекомендуется для использования при работе с детьми, плохо запоминающими большие объемы информации. В этом случае установка на запоминание ребенку дается порциями, начиная с самых сложных случав: 9 • 9,9 • 8,9 • 7. Таким образом, ребенок с ограниченным объемом запоминания запомнит сначала самые сложные случаи, а более легкие случаи таблицы чисел 2,3 и 4 он может получать приемом сложения одинаковых слагаемых или любым другим приемом.
10. Пальцевый счет при запоминании таблицы умножения
Прием пальцевого счета при получении значений табличного умножения мало известен среди учителей начальных классов, хотя является одним из древнейших вычислительных приемов. Следует заметить, что многие учителя не признают правомочности приемов пальцевого счета при изучении табличного сложения и табличного умножения, придерживаясь мнения, что их результаты необходимо учить наизусть. На самом деле многие дети не могут твердо освоить весь объем таблицы умножения именно по причине неумения использовать приемы, помогающие ее освоению. Выучить всю таблицу наизусть могут не все дети. Учителя математики знают, что и среди школьников средних и даже старших классов имеется достаточное количество детей, плохо знающих таблицу умножения.
Для детей младшего школьного возраста с преобладающим ки-нестезическим восприятием и кинестезической памятью прием пальцевого счета при освоении таблицы умножения может быть рекомендован как вспомогательный. Для того чтобы его эффективно использовать, следует знать результаты табличного умножения в пределах таблицы умножения числа 4.
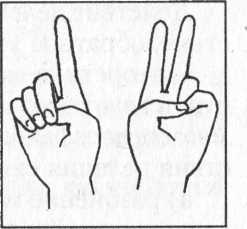
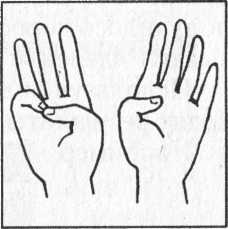
Например, нужно умножить 6 на 7. Зажимаем пальцы на обеих руках в кулак, а затем на каждой руке отгибаем столько пальцев, на сколько каждый множитель больше, чем пять.
|
|
|
На двух руках отогнуто три пальца—это число десятков в искомом числе. На одной руке остались прижатыми к ладони три пальца, на другой — четыре пальца. Эти числа перемножаем 3 • 4 = 12 и прибавляем к числу имеющихся десятков. 30 + 12 = 42. Ответ: 6 • 7 = 42.
Еще один пример: необходимо умножить 8 на 9.
Отгибаем на одной руке три пальца, а на другой руке — четыре пальца (на столько каждый множитель больше, чем пять).
Отогнуто 7 пальцев — это десятки в искомом числе. Перемножаем число загнутых пальцев обеих рук: 2 1 = 2. Прибавляем это количество к числу десятков 70 + 2 = 72. Таким образом 9 • 8 = 72.
11. Мнемонические приемы при заучивании таблицы умножения
Мнемонические приемы при заучивании таблицы умножения сходны с приемами заучивания иностранных слов. Это могут быть карточки с записями табличных случаев, которые ребенок носит в кармане и просматривает при любом удобном случае (в транспорте, в очереди и т. п.).
Карточки лучше делать двусторонними: с одной стороны табличный случай, ас другой — ответ.
Карточки с записью «порции» для заучивания можно развешивать в местах, где ребенок их чаще увидит: над его столом, в ванной у зеркала, в кухне возле его места и т. п.
В любом случае следует учесть, что процесс должен быть распределен во времени, требует многократных повторов и подкрепления любыми из приведенных выше приемов, облегчающих заучивание таблицы.
Лекция 11. Деление
1. Смысл действия деления.
2. Табличное деление.
3. Приемы запоминания таблицы деления.
Смысл действия деления
Действие деления рассматривается в начальной школе как действие, обратное умножению.
С теоретико-множественной точки зрения смыслу деления соответствует операция разбиения множества на равночисленные под-множества. Таким образом, процесс нахождения результатов действия деления связан с предметными действиями двух видов:
а) разбиение множества на равные части (например, 8 кружков разложили в 4 коробки поровну — раскладывают 8 кружков по одному в 4 коробки, а затем считают, сколько кружков получилось в каждой коробке);
б) разбиение множества на части по сколько-то в каждой части (например, 8 кружков разложили в коробки по 4 штуки — раскладывают 8 кружков по 4 штуки в коробки, а затем считают, сколько получилось коробок; деление по этому принципу в методике называют «деление по содержанию»).
Используя подобные предметные действия и рисунки, дети находят результаты деления. Например:
3:2 =... 6:3 =...
Выражение вида 12: 6 называют частным.
Число 12 в этой записи называют делимым, а число 6 — делителем.
|
|
|
Запись вида 12: 6 = 2 называют равенством. Число 2 называют значением выражения. Поскольку число 2 в данном случае получено в результате деления, его также часто называют частным.
Например:
Найдите частное чисел 10 и 5. (Частное чисел 10и 5 —это 2.)
Поскольку названия компонентов действия деления вводятся по соглашению (детям сообщаются эти названия и их необходимо запомнить), педагог активно использует задания, требующие распознавания компонентов действий и употребления их названий в речи.
Например:
1. Среди данных выражений найдите такие, в которых делитель равен 3:
2:2 6:3 6:2 10:5 3:1 3-2 15:3 3-4
2. Составьте частное, в котором делимое равно 15. Найдите его значение.
3. Выберите примеры, в которых частное равно 6. Подчеркните их красным цветом. Выберите примеры, в которых частное равно 2. Подчеркните их синим цветом.
4. Как называют число 4 в выражении 20: 4? Как называют число 20? Найдите частное. Составьте пример, в котором частное равно тому же числу, а делимое и делитель — другие.
5. Делимое 8, делитель 2. Найдите частное.
В 3 классе дети знакомятся с правилом взаимосвязи компонентов деления, которое является основой для обучения нахождению неизвестных компонентов деления при решении уравнений:
Если делитель умножить на частное, то получится делимое.
Если делимое разделить на частное, то получится делитель. (
Например:
Решите уравнение 16: х= 2. (В уравнении неизвестен делитель. Чтобы найти неизвестный делитель, нужно делимое разделить на частное. х = 16: 2, х = 8.)
Однако, данные правила в учебнике математики 3 класса не являются обобщением представлений ребенка о способах проверки действия деления. Правило проверки результатов деления рассматривается в учебнике после знакомства с внетабличным умножением и делением (знакомства с умножением и делением двузначных чисел на однозначные, не входящим в таблицу умножения и деления), перед последним самым трудным случаем вида 87: 29. Это объясняется тем, что получение результатов деления в этом случае представляет собой сложный процесс подбора частного с постоянной его проверкой умножением, поэтому правило проверки действия деления дети рассматривают даже раньше, чем правило проверки действия умножения.
Правило проверки действия деления:
1) Частное умножают на делитель.
2) Сравнивают полученный результат с делимым. Если эти числа равны, деление выполнено верно.
Например: 78: 3 = 26. Проверка: 1) 26 • 3 - 78; 2) 78 - 78.
Табличное деление
В начальной школе действие деления рассматривают как действие обратное умножению. В связи с этим сначала дети знакомятся со случаями деления без остатка в пределах 100 — так называемым табличным делением. С действием деления дети знакомятся после того, как уже выучили наизусть таблицы умножения чисел 2 и 3. На основе знания этих таблиц уже на четвертом уроке после знакомства с делением, составляется первая таблица деления на 2.
2/2=… 8/2=…. 14/2=…
4/2=… 10/2=… 16/2=…
Значения частных в этой таблице получают подсчетом элементов рисунка на картинке.
Следующая таблица деления — деление на 3 является последней таблицей, изучаемой во втором классе. Составляется эта таблица на основе взаимосвязи компонентов умножения с использованием правила нахождения неизвестного множителя. В связи с тем, что данное правило в явном виде предлагается детям в полной формулировке только в 3 классе, на этапе составления таблицы деления на 3 по-прежнему целесообразнее опираться на предметную модель действия (модель на фланелеграфе или рисунок).
Например:
Вычисли и запомни результаты действий. Для проверки ис-
пользуй рисунок:
| 3•3=... | 9:3=... |
| 4•3 =... | 12:3 =... |
| 5•3 =... | 15:3 =... |
| 6•3 =... | 18:3 =.... |
| 7•3 =... | 21:3 =.... |
| 8•3 =... | 24: 3 =... |
| 9•3 =... | 27: 3 =... |
Использование такого рисунка дает возможность составить и третий, взаимосвязанный с первыми двумя, случай деления (третий столбик). Он не относится к таблице деления на 3, но является членом взаимосвязанной тройки, который легче запоминать, ориентируясь на первые два случая. Такой прием запоминания таблицы деления (ориентир на взаимосвязанную тройку) является удобным мнемоническим приемом. Можно видеть, как дети пользуются им, реально запоминая только один прием действия умножения.
Все остальные таблицы деления изучаются в 3 классе. Поскольку умножение числа 4 и умножение на 4 также изучается уже в 3 классе, на этом году обучения прекращается практика раздельного изучения таблиц умножения и деления. Начиная с таблицы умножения числа 4, взаимосвязанные с ней таблицы деления изучают на одном уроке, сразу составляя четыре взаимосвязанных столбика случаев умножения и деления.
Используя результаты первого столбика, дети получают второй столбик перестановкой множителей, а результаты третьего и четвертого столбиков — на основе правила взаимосвязи компонентов умножения:
Если произведение разделить на один из множителей, то получится другой множитель.
Все остальные таблицы деления получают аналогичным способом.
|
|
|


