 |
P(t) = exp{- ∫ λ(t) dt}(6.22) t1
|
|
|
|
∞
T0 = ∫ exp(-λ t) dt = 1/λ. (6. 15)
Поэтому функцию надежности можно записать и так:
Р(t) = еxp(-t/T0). (6. 16)
Если время работы элемента мало по сравнению со средним временем жизни, то можно использовать приближенную формулу
Р(t) ≈ 1 – t/T0. (6. 17)
Среднее время безотказной работы (Т0) является важнейшим показателем невосстанавливаемого элемента, которое определяют как математическое ожидание случайной величины
∞
Т0 = M [τ ] = ∫ tf (t) dt. (6. 18) 0
После преобразования:
∞ ∞ ∞ ∞
T0 = ∫ t f (t) dt = - t P(t)│ + ∫ P(t) dt = ∫ P(t) dt. (6. 19)
0 0 0 0
Среднее время безотказной работы и среднюю наработку до отказа можно получить по результатам испытаний. Для этого нужно проводить испытания до тех пор, пока не откажет последний из элементов. Пусть время жизни каждого из элементов соответственно равно τ 1, τ 2, ... , τ 3. Тогда средняя наработка до отказа
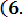
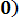
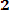
Т0 = (τ 1 + τ 2 + … + τ n) / N = (1/N ) 
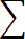

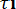


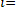
Если испытаниям подвергают N элементов и τ 1, τ 2, …τ N —время их жизни, то статистическую дисперсию находят из выражения
N
S2 = 1/(N – 1) Σ (τ i - τ )2, (6. 21) i=1 где τ = (1/N) Σ τ i.
|
|
|
На практике в качестве оценки надежности чаще используют среднее квадратическое отклонение (σ ), которое определяют как корень квадратный из дисперсии:
σ [τ ]= (D[τ ])2.
Пример 6. 1. На испытания поставлено N =100 элементов. Испытания проводились в течение t = 200 ч. В процессе проведения испытаний отказало n = 5 элементов, при этом отказы зафиксированы в следующие моменты:
τ 1 = 50 ч; τ 2 = 80 ч; τ 3 = 90ч; τ 4 = 100 ч; τ 5 = 150 ч;
остальные элементы не отказали. Определить среднюю наработку до
отказа Т0.
Решение. Для решения задачи воспользуемся формулой () T0 =[(50+80+90+100+150)+(100-5)200]/100 =194. 7 ч. Ответ: T0 = 194. 7ч.
Вероятность безотказной работы в интервале (t1, t2) выражается зависимостью
t2
P(t) = exp{- ∫ λ (t) dt}(6. 22) t1
Функция λ (t) может быть определена по результатам испытаний. Предположим, что испытаниям подвергают N элементов. Пусть n(t) — число элементов, не отказавших к моменту t. Тогда при достаточно малом Δ t и достаточно большом N получим
λ (t) = Δ n/[Δ t n(t)], (6. 23) где Δ n — число отказов на участке Δ t.
Пример 6. 2. По данным эксплуатации генератора установлено, что наработка до отказа подчиняется экспоненциальному закону с параметром λ = 2. 10-5 1/час.
Найти вероятность безотказной работы за время t = 100 часов.
Определить математическое ожидание наработки до отказа. Решение.
Определим вероятность безотказной работы по формуле:
P(t) = e- λ t = exp(-2. 10-5. 100) = 0, 998.
Математическое ожидание наработки до отказа определяем по формуле:
M0 = 1/λ = 1/(2. 10-5) = 5. 104 ч.
Ответ: P(t) = 0, 998; M0 = 5. 104 ч.
Пример 6. 3. Построить кривую интенсивности отказов по данным табл. На испытания поставлено N элементов (N = 200), испытания проводились в течение t = 100 ч.
Таблица 6. 1.
Результаты испытаний элемента (к примеру 6. 3. )
|
|
|
| № п/п | Δ t, ч | Δ n | n(t) | № п/п | Δ t, ч | Δ n | n(t) |
| 0-10 10-20 20-30 30-40 40-50 | 50-60 60-70 70-80 80-90 90-100 |
Обозначения: Δ t — интервал испытаний; Δ n — число отказов; n(t) — число неотказавших элементов.
Для построения кривой (рис. ) вычислим интенсивность отказов λ (ti) ч-1 по формуле
(6. 25): λ (t1) = 10/(10. 190) = 0, 0052; λ (t2) = 8/(10. 182) = 0, 0044; λ (t3) = 6/(10. 176) = 0, 0034; λ (t4) = 4/(10. 172) = 0, 0023; λ (t5) = 2/(10. 170) = 0, 0011; λ (t6) = 2/(10. 168) = 0, 0011; λ (t7) = 2/(10. 166) = 0, 0012; λ (t8) = 4/(10. 162) = 0, 0024; λ (t9) = 5/(10. 157) = 0, 0032; λ (t10) = 8/(10. 149) = 0, 0053.
λ (t)10-3, ч-1
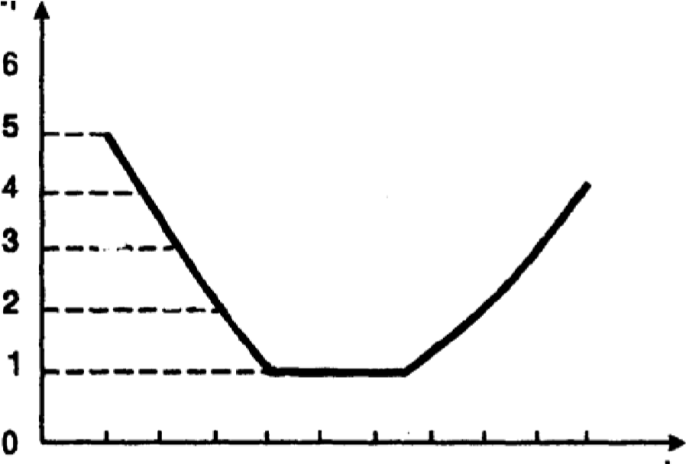
20 40 60 80 100 t, ч
Рис. Кривая интенсивности отказов во времени
Лекция 7 Показатели надежности восстанавливаемых объектов
7. 1. Показатели надежности восстанавливаемого объекта (элемента)
Большинство сложных технических систем с длительными сроками службы являются восстанавливаемыми, т. е. возникающие в процессе эксплуатации отказы систем устраняют при ремонте. Технически исправное состояние изделий в процессе эксплуатации поддерживают проведением профилактических и восстановительных работ.
Для осуществляемых в процессе эксплуатации изделий работ по поддержанию и восстановлению их работоспособности характерны значительные затраты труда, материальныхсредств и времени. Как правило, эти затраты за время эксплуатации изделия значительно превышают соответствующие затраты на его изготовление. Совокупность работ по поддержанию и восстановлению работоспособности и ресурса изделий подразделяют на техническое обслуживание, и ремонт, которые, в свою очередь, подразделяют на профилактические работы, осуществляемые в плановом порядке и аварийные, проводимые по мере возникновения отказов или аварийных ситуаций.
Свойство ремонтопригодности изделий влияет на материальные затраты и длительность простоев в процессе эксплуатации. Ремонтопригодность тесно связана с безотказностью и долговечностью изделий. Так, для изделий, с высоким уровнем безотказности, как правило, характерны низкие затраты труда и средств на поддержание их работоспособности.
Показатели безотказности и ремонтопригодности изделий являются составными частями комплексных показателей, таких как коэффициенты готовности Кг . и технического обслуживания Кт. и. .
|
|
|
К показателям надежности, присущим только восстанавливаемым элементам, следует отнести среднюю наработку на отказ, наработку между отказами, вероятность восстановления, среднее время восстановления, коэффициент готовности и коэффициент технического использования.
Средняя наработка на отказ — наработка восстанавливаемого элемента, приходящаяся, в среднем, на один отказ в рассматриваемом интервале суммарной наработки или определенной продолжительности эксплуатации:
|
|
|


