 |
Dx = f (x)dx. (8.7). F x =ax3 при при. f(x)=dF/dx 3ax2 при при. 0 при х ax при 0. M = ∫ xf x dx = ∫ xaxdx = a /3
|
|
|
|
Dx= 2 (8. 6)
Для непрерывной случайной величины дисперсия определяется из выражения
2
Dx = f (x)dx. (8. 7)
Оценка дисперсии случайной величины:
- 2
Dx* = (1/n-1) 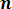
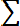

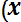
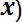
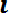


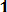
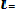
 (8. 8)
(8. 8)
Дисперсия случайной величины является характеристикой рассеяния — разбросанности значений случайной величины около ее математического ожидания. Размерность дисперсии соответствует квадрату размерности случайной величины. Для наглядности в качестве характеристики рассеяния удобнее использовать величину, размерность которой совпадает с размерностью случайной величины. Такой характеристикой может быть среднее квадратическое отклонение σ x, которое определяется как корень квадратный из дисперсии:
σ х = √ Dx . (8. 9)
Для оценки рассеяния с помощью безразмерной величины используют коэффициент вариации, который равен:
ʋ х = σ х / Мх. (8. 10)
Модой случайной величины называют ее наиболее вероятное значение или то ее значение, при котором плотность вероятности максимальна.
Медиана характеризует расположение центра группирования случайной величины.
Площадь под графиком функции плотности распределения делится медианой пополам.
Квантиль — значение случайной величины, соответствующее заданной вероятности.
Квантиль, соответствующую вероятности 0, 5, называют медианой.
Аналогично предыдущим характеристикам понятия моды и медианы даны в статистической трактовке. Для симметричного модального (т. е. имеющего один максимум) распределения математическое ожидание, мода и медиана совпадают.
|
|
|
Пример 8. 1. Функция распределения непрерывной случайной величины
Х задана выражением
при 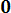
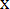


F x =ax3 при при
Найти коэффициент а и плотность распределения f(x).
Р е ш е н и е. Так как функция распределения случайной величины Х непрерывна, то при х= 1, а. х3 = 1, откуда а = 1.
Плотность распределения выражается соотношением
при 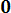
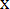


f(x)=dF/dx 3ax2 при при
Пример 8. 2. Плотность распределения случайной величины Х описывается выражением
0 при х ax при 0
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины.
Р е ш е н и е. Математическое ожидание найдем по формуле (7. 4):
1 1
M = ∫ xf x dx = ∫ xaxdx = a /3
0 0
Для определения дисперсии используем формулу (5. 7):
1
Dx = ∫ (x – a2/3)axdx = a(1/4 – 2a/9 +a2/18).
Среднее квадратическое отклонение соответственно равно:
σ x = √ Dx √ a(1/4 – 2a/9 +a2/18).
Пример 8. 3. При проведении одного опыта может появиться или не появиться некоторое событие А. Вероятность появления события А равна р, а вероятность непоявления этого события - 1- p = q.
Определить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х — число появлений события А.
Р е ш е н и е. Ряд распределения случайной величины Х можно записать в виде таблицы:
xi 0 1 pi q p
По формуле (7. 3) находим математическое ожидание:
Mx = = 0q + 1p = p.
Дисперсию величины Х определим по формуле (5. 6).
Dx = ∑ (xi – Mx)2 pi = pq
Среднее квадратическое отклонение равно:
|
|
|
σ = 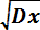
=
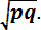
Пример 8. 4. При эксплуатации сложной технической системы получены статистические данные, которые сведены в таблицу. Определить коэффициент готовности системы.
Таблица
Статистические данные, полученные при эксплуатации сложной технической системы
Номер Число отказов Время, ч
системы, mi восстановление Работы, tр Суммарное
п. п отказа, tв, i восстановление
mitв, i
| 1 2 2 5 3 6 4 4 5 8 6 10 7 15 8 20 | |||
| Всего 70 Наработка на отказ | - | ||
| 8 8 | |||
Tо = Σ tр/Σ mi = 4400/70 = 62, 8 ч.
i=1 i=1
Среднее время восстановления
8 8
Tв = Σ mi tв. i/Σ mi = 204/70 = 2, 9 ч.
i=1 i=1
По формуле (8. 3) по вычисленным значениям Tо и Tв находим коэффициент готовности системы:
Кr= 62, 8/(62, 8+2, 9) = 0, 95
|
|
|


