 |
Среднее значение вероятности безошибочной работы оператора
|
|
|
|
Среднее значение вероятности безошибочной работы оператора
Pоп = 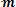
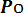

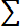
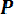

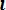






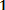
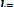

где Рi – вероятность наступления i-го состояния СЧМ;
Pоп/ i – условная вероятность безошибочной работы оператора в i- м состоянии; m – число рассматриваемых состояний СЧМ.
Для систем непрерывного типа показателем надёжности является вероятность безотказного, безошибочного и своевременного протекания производственного процесса в течение времени t
Pч. м1(t) = Pт (t) +[1- Pт (t) ]Kоп [PопPсв + (1- Pоп ) Pисп (tл ) ], где Рт (t) – вероятность безотказной работы технических средств; Kоп – коэффициент готовности оператора;
Рсв – вероятность своевременного выполнения оператором требуемых действий;
Рисп – вероятность исправления ошибочных действий.
Для СЧМ дискретного типа:
Pч. м2 = Kг Pт Роп Pсв + (1- Pт Kг ) Pвос Pоп Pсв + (1- Pоп ) Pт Pисп, где Kг – коэффициент готовности техники;
Рвос – вероятность восстановления отказавшей техники.
Вероятность Pч. м1 используется в случаях, если:
1) технические средства работают исправно; 2) произошёл отказ технических средств, но при этом:
а) оператор безошибочно и своевременно выполнил требуемые действия по ликвидации аварийной обстановки;
б) оператор допустил ошибочные действия, но своевременно их исправил.
Показатель надёжности Pч. м2 используется, если:
1) в требуемый момент времени техника находится в исправном состоянии, не отказала в течение времени выполнения задачи, действия оператора были безошибочными и своевременными;
2) неготовая или отказавшая техника была своевременно восстановлена, операторы при решении задачи не допускали ошибок;
3) при безотказной работе техники оператор допустил ошибку, но своевременно исправил её.
|
|
|
Лекция 12
Логико-графические методы анализа надёжности и риска
12. 1. Понятия дерева отказов: определения и символы
Анализ причин промышленных аварий показывает, что возникновение и развитие крупных аварий, как правило, характеризуется комбинацией случайных локальных событий, возникающих с различной частотой на разных стадиях аварии (отказы оборудования, человеческие ошибки при эксплуатации/ проектировании, внешние воздействия, разрушение /разгерметизация, выброс/ утечка, пролив вещества, испарение, рассеяние веществ, воспламенение, взрыв, интоксикация и т. д. ). Для выявления причинно-следственных связей между этими событиями используют логикографические методы деревьев отказов и событий.
Широкое распространение получили диаграммы в форме потоковых графов (графов состояний и переходов), деревьев событий, отказов (целей, свойств) и функциональных сетей различного предназначения и структуры.
Наиболее широко используемым типом диаграмм влияния являются «деревья». В безопасности диаграммы данного класса часто называют «деревом происшествий» и «деревом их исходов». Они являются в сущности графами с ветвящейся структурой и с дополнительными (логическими) условиями.
Основные достоинства этих моделей:
- сравнительная простота построения;
- дедуктивный характер выявления причинно-следственных связей исследуемых явлений;
- направленность их на существенные факторы;
- легкость преобразования таких моделей;
- наглядность реакции изучаемой системы на изменение структуры;
- возможность качественного анализа исследуемых процессов;
- легкость дальнейшей формализации и алгоритмизации;
- приспособленность к обработке на средствах ВТ (вычислительная техника);
- доступность для статистического моделирования и количественной оценки изучаемых явлений, процессов и их свойств.
|
|
|
Создание «дерева» заключается в определении структуры происшествия:
- элементов – головного события (происшествия) и ему предшествующих предпосылок;
- связей между ними – логических условий, соблюдение которых необходимо и достаточно для его возникновения.
На практике обычно используют обратную или прямую последовательность выявления условий возникновения конкретных происшествий или аварийности и травматизма в целом:
а) от головного события дедуктив но к отдельным предпосылкам;
б) от отдельных предпосылок индуктивно к головному событию.
Из анализа структуры диаграммы влияния (рис. 12. 1) следует, что основными ее компонентами служат узлы (вершины) и связи (отношения) между ними. В качестве узлов обычно подразумеваются простейшие элементы моделируемых категорий (переменные или константы) – события, состояния, свойства, а в качестве связей – активности, работы, ресурсы и другие взаимодействия. Отношения или связи между переменными или константами в узлах диаграммы графически представляются в виде линий, называемых дугами или ребрами.
D =
E1*E2(E3+E4)
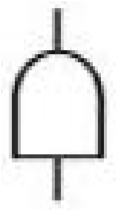
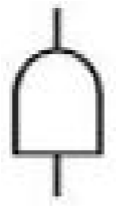
| E |
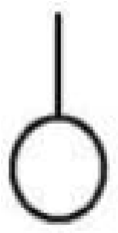
| Е |

| E |
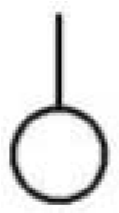
| E |
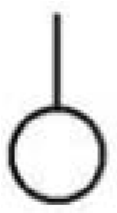
| B = E |
| *E |
| C = E |
| + |
| E |
|
|
|


